Самое большое простое число какое: Математики назвали самое большое простое число // Смотрим

Математик из США открыл самое большое простое число — РБК

www.adv.rbc.ru

www.adv.rbc.ru

www.adv.rbc.ru

Скрыть баннеры

Ваше местоположение ?

ДаВыбрать другое

Рубрики

Курс евро на 6 октября
EUR ЦБ: 58,06

(+1,89)

Инвестиции, 05 окт, 16:23

Курс доллара на 6 октября
USD ЦБ: 59,4

(+0,61)

Инвестиции, 05 окт, 16:23

Клишас заявил, что указ об отсрочке для студентов имеет обратную силу

Политика, 10:50

Военная операция на Украине. Главное

Политика, 10:48

Кортеж вице-президента США попал в ДТП в Вашингтоне. Видео

Политика, 10:47

www.adv.rbc.ru

www.adv.rbc.ru

Почему штраф за отсутствие ОСАГО должен быть равен цене полиса

Партнерский проект, 10:39

Мобилизованным не компенсируют расходы на дополнительную экипировку

Общество, 10:38

Навка назвала детским садом новый конфликт Плющенко и Ягудина

Спорт, 10:36

Что поможет распознать неэффективного сотрудника на собеседовании

Pro, 10:33

Объясняем, что значат новости

Вечерняя рассылка РБК

Подпишитесь за 99 ₽ в месяц

На въезде в Грозный установили 15-метровые песочные часы

Общество, 10:28

В чем важность цифровых сервисов во время переориентации экспорта

РБК+, 10:28

Овечкин забросил первую шайбу после возвращения из Москвы в Вашингтон

Спорт, 10:27

Хватит ли IT-специалистов для развития бизнеса в России

РБК и S+Консалтинг, 10:16

Bloomberg не исключил сокращения добычи нефти Россией из-за «потолка цен»

Политика, 10:14

Микрозаймы и краудинвестинг: что нужно знать о поддержке малого бизнеса

Национальные проекты, 10:10

В МИД заявили о «размытии» нейтралитета Австрии из-за поддержки санкций

Политика, 10:10

www. adv.rbc.ru

www.adv.rbc.ru

www.adv.rbc.ru

Американский математик открыл на данный момент самое большое простое число – так называемое 48-е число Мерсенна. Об этом в четверг сообщает Great Internet Mersenne Prime Search (GIMPS).

Фото: РБК

Открытие совершил ученый из Миссури (США), доктор наук Куртис Купер. Найденное им число в десятичной записи составляет 17 425 170 символа. Для сравнения, предыдущее можно было записать, используя 12 978 189 символов.

Напомним, что простым числом в математике называется то число, которое делится на единицу и на само себя, таким образом имея только два делителя. Кроме того, существуют так называемые простые числа специального вида, то есть такие, простота которых устанавливается с использованием специализированных алгоритмов. Числа Мерсенна как раз относятся к простым числам специального вида, они встречаются крайне редко – современной науке известны только 48. Из них последние 14 были открыты в GIMPS.

Доктор Купер не в первый раз делает подобные открытия – это уже третье самое большое простое число, открытое им. Первый его рекорд был зарегистрирован в США в 2005г., затем в 2006г. Череду побед американского ученого прервал чужой рекорд, одержанный компьютером в Лос-Анджелесе в 2008г. Сегодняшним открытием доктор Купер вернул себе первенство.

www.adv.rbc.ru

Чтобы доказать, что открытое число действительно является простым, К.Куперу понадобилось 39 дней вычислений на одном из ПК университета. Одновременно сразу три машины осуществляли проверку полученных данных.

www.adv.rbc.ru

Числа Мерсенна названы в честь французского математика Марена Мерсенна, их последовательность начинается как 1, 3, 7, 15, 31, 63, 127, 255. Они получили известность в связи с эффективным критерием простоты Люка — Лемера, благодаря которому числа Мерсенна давно удерживают лидерство как самые большие известные простые числа. На практике они применяются для построения генераторов псевдо-случайных чисел с большими периодами, в качестве примера можно привести вихрь Мерсенна.

Между строк текст песни Самое Большое Простое Число

Посмотреть все тексты песен СБПЧ

Если просто мне было все время лень

Если стыдно мне было за эту лень

Если дольше столетия длится день

То, где же тогда благодать?

Если там нас, похоже, никто не ждет

Если это был тонкий, но все же лед

Если смелым, но глупым был наш расчет

То к черту вообще умирать

И между глаз и между строк

И не кончается урок

И между строк и между глаз

И между позже и сейчас

И между завтра и потом

Мы все когда-нибудь умрем

И между умер и продрог

И между глаз и между строк

Если просто все было все время зря

Если это закат был, а не заря

Если все вопреки, не благодаря

Какой же смысл в борьбе?

Я мечтал делать просто не только для

Мне не надо ни пороха, ни огня

Но я точно уверен не вспомню дня

Чтоб не думал я о тебе

И между глаз и между строк

И не кончается урок

И между строк и между глаз

И между позже и сейчас

И между завтра и потом

Мы все когда-нибудь умрем

И между умер и продрог

И между глаз и между строк

И между глаз и между строк

И не кончается урок

И между строк и между глаз

И между позже и сейчас

И между завтра и потом

Мы все когда-нибудь умрем

И между умер и продрог

И между глаз и между строк

Понравился текст песни?

Оставьте комментарий ниже

Исправить текстПосмотреть все тексты песен СБПЧ

Поделитесь ссылкой на текст:

Рейтинг текста:

1. Text-pesni. com
2. С
3. СБПЧ
4. Между строк (Самое Большое Простое Число)

Популярные тексты и переводы песен исполнителя СБПЧ:

Злой (Самое большое простое число)


СБПЧ

Нежно (Самое большое простое число)


СБПЧ

Комната


СБПЧ

Кому (Самое большое простое число)


СБПЧ

Песня зеркальца обо всем (Самое большое простое число)


СБПЧ

Популярные тексты и переводы песен:

ЛП (ft. Milana Star)


Милана Хаметова

Ұстазым (Устазым, Ұстазым менің ұстазым)


Ақбота Керімбекова

Скажи мне/Asa du


JANAGA

Черная Любовь (ft. MONA)


ELMAN

Твоя нежная походка (Той зимой недалекой)


Тимур Муцураев

Fire man (Мияги, Фая ман, Fireball, Замкнутыми стенами давила та печаль)


MiyaGi & Эндшпиль

Учителя (Ермолов, Пора наступает осенняя)


Школьные песни

Голова (ft. Galust)


Канги

Нити


Loc-Dog

Малиновая лада (Пусть луна нам светит ярко)


GAYAZOV$ BROTHER$

Лучшие тексты и переводы песен:

Сияй (Рамиль)


Ramil’

Дико тусим (ft. Николай Басков)


Даня Милохин

Если тебе будет грустно (ft. NILETTO, Рауф и Фаик, Нилетто)


Rauf & Faik

Юность (Добро, Звук поставим на всю соседи не спят)


Dabro

Лютики (Я смотрю наши старые мультики)


Просто Лера

Снова я напиваюсь (Слава Марлов)


Slava Marlow

Fendi (Рахим Фенди худи Гуччи Прада Луи на мне)


Rakhim

Поболело и прошло (Да подальше все пошло)


HENSY

неболей (ft. Zivert, Зиверт, не болей, С неба лей)


Баста

Танцевать вот так (Из тик тока Дрим Тима)


Ваша Маруся

Похожие тексты и переводы песен:

Между строк (Самое Большое Простое Число)


СБПЧ

Кому (Самое большое простое число)


СБПЧ

Герой (Самое большое простое число)


СБПЧ

Бульдозер (Самое большое простое число)


СБПЧ

Надоел (Самое Большое Простое Число)


СБПЧ

«Самое Большое Простое Число» («СБПЧ») – история создания, группа, фото, альбомы, состав, Кирилл Иванов 2022

Биография

«Самое Большое Простое Число» — российская музыкальная группа, которую сокращенно называют «СБПЧ». Специфическая музыка в исполнении участников команды и инфантильные стихи пришлись по душе прогрессивной молодой публике. Коллектив часто экспериментировал, пробовал себя в разных жанровых ипостасях, что помогло ему в короткие сроки обрести внушительную армию поклонников.

История создания и состав

История создания проекта уходит корнями в начало «нулевых». Встретившись в Санкт-Петербурге, Кирилл Иванов и «Елочные игрушки» образовали первый состав команды. Название для группы придумал Иванов. Он преследовал 2 цели: трансформацию наименования и использование цифрового эквивалента. Первая идея выглядела так: «232 582 657 – 1». Эта комбинация представляла собой самое большое известное простое число. Но постепенно происходили открытия новых простых чисел, и эта подборка цифр становилась неактуальной. Тогда музыканты перешли к словесному воплощению идеи.

Концепция «Самого Большого Простого Числа» заключалась в отсутствии ударных, эффект которых возмещали ритм мелодии и речитатив. Симбиоз мощного и хрупкого виделся фронтмену идеальным сочетанием, которое дополняла отстраненность текста.

Группа прошла несколько этапов становления, начиная путь от оркестра из 17 исполнителей. Эксперименты с большим количеством музыкантов закончились в конце «нулевых». В 2009 году в составе команды, помимо Кирилла Иванова в роли вокалиста, остались Илья Барамия в качестве басиста и Александр Зайцев, выполняющий функции гитариста и второго вокалиста. В 2018-м к группе присоединилась солистка Женя Борзых, а место Барамии занял Станислав Астахов.

Музыка

В 2006-м музыканты впервые посетили фестиваль «Нашествие» как приглашенные участники. Иванов выступал совместно с «Елочными игрушками» и коллективом «2H COMPANY». Публика восприняла их появление на сцене благосклонно, что стало успехом для команды, несущей в массы своеобразную стилистику и звучание.

Дебютная пластинка передавалась из рук в руки, пока не попала к продюсеру Олегу Нестерову. Он помог с изданием альбома. Музыканты выпустили его при поддержке лейбла «Снегири» в 2007 году. Диск получил лестные комментарии от критиков, а журнал GQ признал Иванова музыкантом года. Любопытно, что работу в музыкальной сфере Кирилл Иванов совмещал с занятостью в роли журналиста. Он работал сюжетным репортером на каналах НТВ и СТС.

Модифицировавшись в «СБПЧ-оркестр», музыканты привлекли к работе несколько артистов и творческих объединений и записали одноименный диск. Коллектив начал давать концерты, а к 2011-му выпустил 3-й альбом. После этого артисты старались ежегодно презентовать свежую пластинку. Иванов отошел от журналистики и сконцентрировался на творчестве группы. В 2012-м вышел диск «Лесной оракул», вдохновленный воспоминаниями о лете в детском лагере. В поддержку альбома сняли клип на песню «Идеальное место».

В 2014-м поклонники встретили альбом «Я думаю, для этого не придумали слово», записанный совместно с Игорем Вдовиным и Надей Грицкевич. В 2015-м дискография пополнилась пластинкой «Здесь и всегда» и свежими хитами. Новинки также вышли в 2016-м, а затем в 2017-м. Тогда же состоялась премьера фильма «Про любовь. Только для взрослых», где в качестве саундтрека звучала песня коллектива.

В 2018-м вышел диск «Мы не спали, мы снились», созданный при участии Жени Борзых, нескольких других музыкантов и вокалистов, а также Детского хора ТВ и радио Санкт-Петербурга. Песню «Провал», включенную в эту пластинку, исполнители представили на шоу «Вечерний Ургант». Команда продолжила писать новые треки и выступать по России с концертами.

Летом 2019-го «СБПЧ» участвовали в эксперименте, выступив на Red Bull Music Festival. В пространстве «Рихтер» группа дала 24-часовой концерт, исполнив песни, выпущенные с момента создания команды. Коллектив появился на сцене совместно с приглашенными артистами, которые успели поработать в нем ранее.

В июле того же года состоялась презентация клипа «Молодость», эстетика которого оказалась современной, молодежной и непонятной приверженцам традиционных видео. По традиции участники проекта порадовали фанатов выходом нового релиза «Злой». Кирилл Иванов часто давал интервью, а в инстаграм-аккаунте группы публиковались актуальные посты и фото музыкантов.

В 2020 году в разгар пандемии коронавируса группа представила публике новый альбом под философским названием «Все равно». Лидер проекта пояснил в интервью, что главной тематикой песен диска стали концепты «жизнь» и «смерть». Это придало релизу, который записывался в ЮАР, особое настроение, созвучное атмосфере тревожности и ажиотажа, вызванной Covid-19.

Помимо самих музыкантов в создании пластинки участвовали приглашенные гости. Так, например, в записи трека «Набор букв» прозвучал голос Александра Гудкова. Кирилл назвал последнего одним из самых самобытных, уникальных комиков нашего времени, а при работе над хитом попросил Сашу оставаться предельно серьезным. Кроме того, яркость альбому придало присутствие темнокожего исполнителя Sandy B родом из Южной Африки.

Работа велась быстро и плодотворно, участники команды, как и прежде, много экспериментировали, пробовали разные стили, играли на контрастах. В композиции «Нежно», например, солистка Евгения поет достаточно быстро и резко, что создало намеренный диссонанс с названием трека.

«Самое Большое Простое Число» сейчас

В 2021 году группа «Самое Большое Простое Число» продолжила творческую деятельность. Осенью музыканты порадовали поклонников новостью о выходе очередного проекта. На этот раз исполнители предложили публике не альбом, а детскую аудиокнигу «Потерянное зеркальце», основанную на сочинении Павла Пепперштейна (Пивоварова), к которой участники «СБПЧ» написали музыку.

В интервью Иванов признался, что хотел создать аудиосказку, подобную произведениям Ганса Христиана Андерсена или Теодора Амадея Гофмана, которые он сам читал с удовольствием. Помимо музыкантов в записи книги участвовали Александр Гудков, Муся Тотибадзе и другие артисты. Сейчас у команды появились идеи в дальнейшем создать по этому проекту театральную постановку и музыкальную киноленту.

Дискография

• 2007 — «Самое большое простое число»
• 2008 — «СБПЧ Оркестр»
• 2011 — «Флешка»
• 2012 — «Лесной оракул»
• 2013 — «СБПЧ и Кассиопея поют песни друг друга»
• 2014 — «Я думаю, для этого не придумали слово»
• 2018 — «Мы не спали, мы снились»
• 2019 — «Наверное, точно»
• 2021 — «Со слов дерева записано верно»

Клипы

• 2008 — «Рождество»
• 2010 — «Блокада»
• 2013 — «Втроем»
• 2013 — «Секрет»
• 2013 — «Идеальное место»
• 2014 — «Выходной»
• 2015 — «Море»
• 2016 — «Суперкит»
• 2016 — «Метеоры, кометы, болиды»
• 2017 — «Динозавр»
• 2018 — «У нас есть все»
• 2018 — «Африка»
• 2019 — «Злой»
• 2019 — «Молодость»
• 2020 — «Нежно»
• 2020 — «Король»
• 2020 — «Прах»

Интересные факты

• По мотивам африканских приключений 2020 года участники «Самого Большого Простого Числа» создали документальный фильм в трех частях.
• Обложку для сингла «Нежно» музыканты заказали у популярного художника из Ганы Дэниеля Анума Джаспера, славящегося рисованием постеров к голливудским фильмам.
• Музыкальные критики окрестили Барамию и Зайцева идейными преемниками Сергея Курехина из группы «Поп-механика», а Кириллу дали характеристику «антимачо».

50-е известное простое число Мерсенна, когда-либо найденное на компьютере, добровольно участвовало в совместном проекте — ScienceDaily

Новости науки

от исследовательских организаций

2

50-е известное простое число Мерсенна, когда-либо найденное, на компьютере добровольно участвовало в совместном проекте

Дата:

4 января 2018 г.

Источник:

Великий поиск простых чисел Мерсенна в Интернете (GIMPS)

Резюме:

Совместный компьютерный проект обнаружил самое большое известное простое число. Новое простое число почти на миллион цифр больше, чем предыдущее рекордное простое число, в особом классе чрезвычайно редких простых чисел, известных как простые числа Мерсенна.

Поделиться:

ПОЛНАЯ ИСТОРИЯ

Великий поиск простых чисел Мерсенна в Интернете (GIMPS) обнаружил самое большое известное простое число 2 ^{77 232 917} -1, имеющее 23 249,425 цифр. Компьютер, предоставленный Джонатаном Пейсом, сделал находку 26 декабря 2017 года. Джонатан — один из тысяч добровольцев, использующих бесплатное программное обеспечение GIMPS.

Новое простое число, также известное как M77232917, вычисляется путем умножения 77 232 917 двоек и последующего вычитания единицы. Это почти на миллион цифр больше, чем предыдущее рекордное простое число, относящееся к особому классу чрезвычайно редких простых чисел, известных как простые числа Мерсенна. Это всего лишь 50-е известное простое число Мерсенна из когда-либо обнаруженных, и найти каждое из них становится все труднее. Простые числа Мерсенна были названы в честь французского монаха Марина Мерсенна, изучавшего эти числа более 350 лет назад. GIMPS, основанная в 1996, обнаружил последние 16 простых чисел Мерсенна. Добровольцы загружают бесплатную программу для поиска этих простых чисел, а каждому, кому посчастливится найти новое простое число, предлагается денежное вознаграждение. Профессор Крис Колдуэлл поддерживает авторитетный веб-сайт, посвященный крупнейшим известным простым числам, и имеет превосходную историю простых чисел Мерсенна.

Доказательство простоты заняло шесть дней безостановочных вычислений на ПК с процессором Intel i5-6600. Чтобы доказать отсутствие ошибок в процессе обнаружения прайма, новый прайм был независимо проверен с использованием четырех разных программ на четырех разных аппаратных конфигурациях.

• Аарон Блоссер проверил это с помощью Prime95 на сервере Intel Xeon за 37 часов.
• Дэвид Стэнфилл проверил это с помощью gpuOwL на графическом процессоре AMD RX Vega 64 за 34 часа.
• Андреас Хеглунд проверил простое число с помощью CUDAlucas, работающего на графическом процессоре NVidia Titan Black, за 73 часа.
• Эрнст Майер также проверил это с помощью собственной программы Mlucas на 32-ядерном сервере Xeon за 82 часа. Андреас Хеглунд также подтвердил, что Mlucas работал на инстансе Amazon AWS за 65 часов.

Джонатан Пейс — 51-летний инженер-электрик, проживающий в Джермантауне, штат Теннесси. Настойчивость Джона наконец окупилась — он охотился за большими простыми числами с помощью GIMPS более 14 лет. Открытие имеет право на получение награды GIMPS за исследовательское открытие в размере 3000 долларов.

Клиентское программное обеспечение GIMPS Prime95 было разработано основателем Джорджем Вольтманом. Скотт Куровски написал системное программное обеспечение PrimeNet, которое координирует работу компьютеров GIMPS. Аарон Блоссер теперь является системным администратором, обновляя и поддерживая PrimeNet по мере необходимости. У добровольцев есть шанс получить вознаграждение за исследовательское открытие в размере 3000 или 50 000 долларов, если их компьютер обнаружит новое простое число Мерсенна. Следующей важной целью GIMPS является получение награды в размере 150 000 долларов США от Electronic Frontier Foundation за поиск 100-миллионного простого числа.

Заслуга в этом прайме принадлежит не только Джонатану Пейсу за запуск программного обеспечения Prime95, Вольтману за написание программного обеспечения, Куровски и Блоссеру за их работу на сервере Primenet, но и тысячам добровольцев GIMPS, которые просеивали миллионы неосновных кандидаты. В знак признания всех вышеперечисленных людей, официальная заслуга в этом открытии принадлежит «Дж. Пейсу, Г. Вольтману, С. Куровски, А. Блоссеру и др.».

The Great Internet Mersenne Prime Search (GIMPS) была создана 19 января.96 Джорджа Вольтмана, чтобы открыть новый мировой рекорд размера простых чисел Мерсенна. В 1997 году Скотт Куровски позволил GIMPS автоматически использовать мощь тысяч обычных компьютеров для поиска этих «иголок в стоге сена». Большинство участников GIMPS присоединяются к поиску острых ощущений от возможного открытия рекордного, редкого и исторического нового простого числа Мерсенна. Поиск других простых чисел Мерсенна уже начался. Могут быть меньшие, еще не открытые простые числа Мерсенна, и почти наверняка есть более крупные простые числа Мерсенна, ожидающие своего открытия. Любой, у кого есть достаточно мощный компьютер, может присоединиться к GIMPS и стать крупным охотником за праймом, а также, возможно, получить денежную награду за исследования. Все необходимое программное обеспечение можно бесплатно загрузить на сайте www.mersenne.org/download/.

изменить ситуацию: спонсируемая возможность

Источник истории:

Материалы предоставлены Great Internet Mersenne Prime Search (GIMPS) . Примечание. Содержимое можно редактировать по стилю и длине.

Цитировать эту страницу :

• MLA
• АПА
• Чикаго

Великий поиск простых чисел Мерсенна в Интернете (GIMPS). «Самое большое известное простое число обнаружено: 50-е известное простое число Мерсенна, когда-либо найденное на компьютере, добровольно участвовало в совместном проекте». ScienceDaily. ScienceDaily, 4 января 2018 г. .

Великий поиск простых чисел Мерсенна в Интернете (GIMPS). (2018, 4 января). Обнаружено самое большое известное простое число: 50-е известное простое число Мерсенна, когда-либо найденное на компьютере, добровольно участвовало в совместном проекте. ScienceDaily . Получено 4 октября 2022 г. с сайта www.sciencedaily.com/releases/2018/01/180104164507.htm

Great Internet Mersenne Prime Search (GIMPS). «Самое большое известное простое число обнаружено: 50-е известное простое число Мерсенна, когда-либо найденное на компьютере, добровольно участвовало в совместном проекте». ScienceDaily. www.sciencedaily.com/releases/2018/01/180104164507.htm (по состоянию на 4 октября 2022 г.).

реклама

Самое большое в мире простое число состоит из 23 249 425 цифр. Вот почему вы должны заботиться.

Шифрование RSA, один из стандартных способов шифрования данных в сети, требует, чтобы пользователь придумал два больших простых числа и перемножил их.

Eyematrix/Thinkstock

Обновление от 4 января 2018 г.: В среду Great Internet Mersenne Prime Search объявил, что компьютер, принадлежащий Джонатану Пейсу в Джермантауне, штат Теннесси, обнаружил новое простое число. В 23 249425 цифр, число, известное как M77232917, теперь является самым большим известным простым числом.

В 2016 году я написал следующую статью о предыдущем самом большом известном простом числе, которое сейчас является вторым по величине известным простым числом. Его имя M74207281, и оно примерно на миллион цифр короче нового блестящего простого числа. Но если не считать нескольких подробностей о том, чей компьютер его нашел и какова его длина, я мог бы сегодня написать эту статью о новом прайме. Поэтому мы снова делимся ею с вами.

Очень интересно найти новое самое большое известное простое число, но это еще один куплет той же песни. Оба числа, как и девять из 10 самых больших известных простых чисел, имеют особую форму и называются простыми числами Мерсенна. Мы находим их, потому что именно там мы продолжаем искать. Свет там лучше. Между этими двумя самыми большими известными простыми числами лежит непостижимое количество чудовищно больших простых чисел; мы можем никогда не найти ни одного.

Оригинал, 22 января 2016 г.: Ранее на этой неделе BBC News сообщила о важном математическом открытии, поделившись новостью под заголовком «Самое большое известное простое число обнаружено в Миссури». Эта формулировка звучит так, будто это новое простое число — между прочим, это 2 ^{74 207 281} -1 — было найдено посреди какой-то дороги под уличным фонарем. На самом деле это не плохой способ думать об этом.

Мы знаем об этом огромном простом числе благодаря Великому поиску простых чисел Мерсенна в Интернете. Охота Мерсенна, известная как GIMPS, представляет собой крупный проект распределенных вычислений, в рамках которого добровольцы запускают программное обеспечение для поиска простых чисел. Возможно, самым известным аналогом является SETI@home, который ищет признаки внеземной жизни. GIMPS добился более ощутимого успеха, чем SETI: на данный момент обнаружено 15 простых чисел. Блестящее новое простое число, получившее очаровательное прозвище M74207281, является четвертым, найденным математиком из Университета Центрального Миссури Кертисом Купером с помощью программного обеспечения GIMPS. Этот состоит из 22 338 618 цифр.

Простое число — это целое число, единственными делителями которого являются 1 и само себя. Числа 2, 3, 5 и 7 простые, а 4 — нет, потому что его можно разложить на множители как 2 x 2. (Из соображений удобства мы не считаем 1 простым.) М в GIMPS и в M74207281 означает Марина Мерсенна, французского монаха 17 ^-го -го века, изучавшего числа, носящие его имя. Числа Мерсенна на 1 меньше, чем степень числа 2. Простые числа Мерсенна, по логике вещей, — это числа Мерсенна, которые также являются простыми. Число 3 — простое число Мерсенна, потому что оно на единицу меньше, чем 2·9.0035 2 , что равно 4. Следующие несколько простых чисел Мерсенна — 7, 31 и 127.

M74207281 — это 49 ^-е известное простое число Мерсенна. Следующее по величине известное простое число 2 ^{57 885 161} -1 также является простым числом Мерсенна. Так и тот, что после этого. И следующий. И следующий. В целом, 11 крупнейших известных простых чисел — это числа Мерсенна.

Почему мы знаем так много больших простых чисел Мерсенна и так мало больших простых чисел Мерсенна? Это не потому, что большие простые числа Мерсенна особенно распространены, и это не впечатляющее совпадение. Это возвращает нас к дороге и уличному фонарю. Существует несколько различных версий этой истории. Мужчина, возможно, пьяный, стоит на четвереньках под уличным фонарем. Добрый прохожий, возможно, полицейский, останавливается, чтобы спросить, что он делает. «Я ищу свои ключи», — отвечает мужчина. — Ты потерял их здесь? — спрашивает офицер. «Нет, я потерял их на улице, — говорит мужчина, — но здесь светлее».

Мы продолжаем находить большие простые числа Мерсенна, потому что там лучше освещено.

Во-первых, мы знаем, что лишь несколько чисел Мерсенна являются кандидатами на то, чтобы быть простыми числами Мерсенна. Показатель степени n в 2 ⁿ -1 должен быть простым, поэтому нам не нужно проверять, например, 2 ⁶ -1. простые показатели более заманчивы, чтобы попробовать. Наконец, есть специальный тест на простоту — тест Лукаса-Лемера, который можно использовать только для чисел Мерсенна.

Чтобы понять, почему тест вообще существует, давайте отвлечемся и посмотрим, почему мы вообще пытаемся найти простые числа. Их бесконечно много, так что вряд ли мы когда-нибудь найдем самую большую. Но помимо того, что это интересно в смысле «математики ради математики», поиск простых чисел — это хороший бизнес. Шифрование RSA, один из стандартных способов шифрования данных в Интернете, требует, чтобы пользователь (возможно, ваш банк или Amazon) придумал два больших простых числа и перемножил их. Если предположить, что шифрование реализовано правильно, сложность факторинга полученного продукта — единственное, что может быть между хакерами и номером вашей кредитной карты.

Это новое простое число Мерсенна не будет использоваться для шифрования в ближайшее время. В настоящее время нам нужны только простые числа длиной в несколько сотен цифр, чтобы сохранить наши секреты в безопасности, поэтому миллионы цифр в M74207281 на данный момент являются излишними.

com/_components/slate-paragraph/instances/cq-article-bfed748c5afea437eac5b800efefbb9c-component-13@published»> Вы не можете просто найти 300-значное простое число в таблице. (Их около 10 ²⁹⁷ . Даже если бы мы захотели, мы физически не смогли бы записать их все.) Чтобы найти большие простые числа для использования в шифровании RSA, нам нужно проверить случайно сгенерированные числа на простоту. Один из способов сделать это — пробное деление: разделите число на меньшие числа и посмотрите, получится ли когда-нибудь обратно целое число. Для больших простых чисел это занимает слишком много времени. Следовательно, существуют тесты простоты, которые могут определить, является ли число простым, фактически не разлагая его на множители. Тест Лукаса-Лемера — один из лучших.

Тепловая смерть Вселенной произойдет раньше, чем мы сможем пройти хотя бы часть пути через пробное деление числа, состоящего из 22 миллионов цифр. Однако компьютеру потребовался всего месяц, чтобы использовать тест Лукаса-Лемера, чтобы определить, что M74207281 является простым числом. Нет других тестов на простоту, которые бы выполнялись почти так же быстро для произвольных 22-миллионных чисел.

Сколько простых чисел мы пропустили, ища их в основном под уличным фонарем Лукаса-Лемера? Мы не знаем точного ответа, но теорема о простых числах подводит нас достаточно близко. Имеет смысл, что простые числа становятся менее распространенными по мере того, как мы блуждаем по числовой прямой. Целых 40 процентов однозначных чисел являются простыми, 22 процента двузначных чисел являются простыми и только 16 процентов трехзначных чисел. Теорема о простых числах, впервые доказанная в конце 1800-х годов, дает количественную оценку этого падения. Это говорит о том, что в общем случае количество простых чисел меньше n стремится к n/ln(n) по мере увеличения n . (Здесь вместо — натуральный логарифм.)

Мы можем использовать теорему о простых числах, чтобы оценить, сколько пропущенных простых чисел находится между M74207281 и следующим наименьшим простым числом. Мы просто подставляем 2 ^{74 207 281} -1 в n/ln(n) и получаем действительно большое число. Мы можем записать его наиболее компактно, сложив экспоненты: 10 ^{10 7,349} . Это число состоит примерно из 22 338 610 цифр, плюс-минус пара, поэтому мы также можем записать его как 10 9.0035 22 338 610 .

Еще одно обращение к теореме о простых числах показывает, что существует примерно на 10 ^{17 425 163} простых чисел меньше, чем следующее по величине известное простое число. Это звучит впечатляюще, пока вы не поймете, что 10 ^{17 425 163} меньше 0,0000000000001 процента от 10 ^{22 338 610} .

Остановись и подумай об этом на мгновение. Существует около 10 ^{22 338 610} простых чисел, меньших, чем M74207281, и примерно все они находятся между ним и следующим по величине известным простым числом. Если вы хотите быть милосердным, вы могли бы сказать, что у нас есть некоторые пробелы в наших знаниях о простых числах. Но на самом деле имеет смысл сказать, что у нас есть пробелы в недостатке знаний. Миллионы и миллионы простых чисел, которые мы уже нашли, составляют примерно 0 процентов простых чисел, меньших M74207281. Каждое из них — это маленькая песчинка, крупица, которая мало чем может скрыть наше непомерное невежество относительно того, где именно живут простые числа.

com/_components/slate-paragraph/instances/cq-article-bfed748c5afea437eac5b800efefbb9c-component-19@published»> Исправление от 22 января 2016 г.: Первоначально в этой статье упоминалось возможное простое число – 2 ^n-1 . Это число должно было отображаться как 2 ⁿ -1. (Возврат.)

Математика

Наука

Это самое большое известное простое число | Умные новости

Питерхауэлл через iStock

Встречайте новое самое большое известное простое число. Оно начинается с 4, продолжается 23 миллионами цифр и заканчивается 1. Как и все простые числа, оно может быть без остатка разделено только на единицу и само на себя.

Простые числа необходимы для современной жизни, они используются во всем: от надежного шифрования банковской информации до генераторов случайных чисел, используемых специалистами по визуальным эффектам для последних фильмов. И хотя нахождение больших простых чисел не обязательно означает более надежное шифрование (это распространенное заблуждение), человеческое любопытство побуждает к постоянному поиску все больших простых чисел.

«Каждое новое простое число — это расширение границ человеческого математического знания», — пишет в электронном письме Смитсоновскому институту исследователь Центра Хартри Иэн Бетьюн, участвующий в проекте по поиску простых чисел PrimeGrid, который не участвовал в новой находке. ком.

Новейшее простое число получается путем умножения двух на себя 77 232 917 раз с последующим вычитанием единицы. В математических терминах это: 2 ^{77 232 917} — 1. Этот формат вычисления означает, что новое простое число считается простым числом Мерсенна. Названные в честь французского теолога и математика Марина Мерсенна, эти типы простых чисел всегда вычисляются как степень двойки минус один. Этот шаблон создает счетный (хотя и огромный) список возможных простых чисел Мерсенна.

Число, которое может быть сокращенно записано как M77232917, почти на миллион цифр длиннее, чем последнее подтвержденное простое число, обнаруженное в 2016 году. Хотя это пятидесятое открытое простое число Мерсенна, не все кандидаты между двумя последними простыми числами еще не проверены, поэтому между ними может скрываться другой. Но это было бы удивительно, говорит Крис Колдуэлл, математик, отслеживающий открытие больших простых чисел. Согласно Колдуэллу, разрыв между простыми числами Мерсенна обычно намного больше.

Когда M77232917 записывается как все 23 249 425 цифр, число содержит каждую цифру от нуля до девяти примерно 2,3 миллиона раз каждая. И, как и все простые числа, оно кажется случайным, хотя некоторые исследователи предполагают, что распределение простых чисел определяется слабыми узорами.

Этих слабых закономерностей достаточно, чтобы сузить поиск новых простых чисел. Это помогает исследователям предсказать, сколько простых чисел будет существовать в диапазоне чисел, объясняет Роберт Лемке Оливер, математик из Университета Таффтса. «Случается, что среди чисел с 1000 цифр примерно одно из каждых 2500 будет простым», — пишет он в электронном письме на Smithsonian.com.

Открытие нового прайма было коллективным усилием. Компьютер, принадлежащий Джонатану Пейсу, инженеру-электрику, живущему в Теннесси, определил номер с помощью специализированного программного обеспечения Great Internet Mersenne Prime Search (GIMPS). Программное обеспечение, разработанное Джорджем Вольтманом, проверяет номера кандидатов в рамках поиска, координируемого системным программным обеспечением PrimeNet, написанным Скоттом Куровски и поддерживаемым Аароном Блоссером. После открытия M77232917 было проверено как простое число Блоссером и тремя другими людьми — Дэвидом Станфиллом, Андреасом Хеглундом и Эрнстом Майером — каждый из которых использовал разное программное обеспечение и компьютерные настройки.

«Что особенного в этом простом, так это не то, что оно простое, а то, что мы действительно знаем, что оно простое»,  – пишет Лемке Оливер. Определить, является ли число простым, концептуально просто. Все, что вам нужно сделать, это разделить его на все простые числа, меньшие, чем он сам. Если никакие другие простые числа не могут разделить его без остатка, это должно быть новое простое число. На практике, однако, этот подход грубой силы требует много времени для очень больших чисел, даже с современными компьютерами, способными к исключительно быстрым вычислениям. Вместо этого алгоритмы используют трюк теории чисел, называемый тестом Лукаса-Лемера, который работает только для простых чисел Мерсенна, чтобы ускорить процесс.

Несмотря на это, проверка кандидатов на простые числа по-прежнему утомительна с вычислительной точки зрения. Компьютеру Пейса потребовалось шесть дней, чтобы обнаружить M77232917; проверки заняли дополнительно 291 вычислительный час. Это открытие является первым для Пейса, который работал с программным обеспечением для поиска больших простых чисел в течение последних 14 лет.

Поиск новых простых чисел — горячая тема.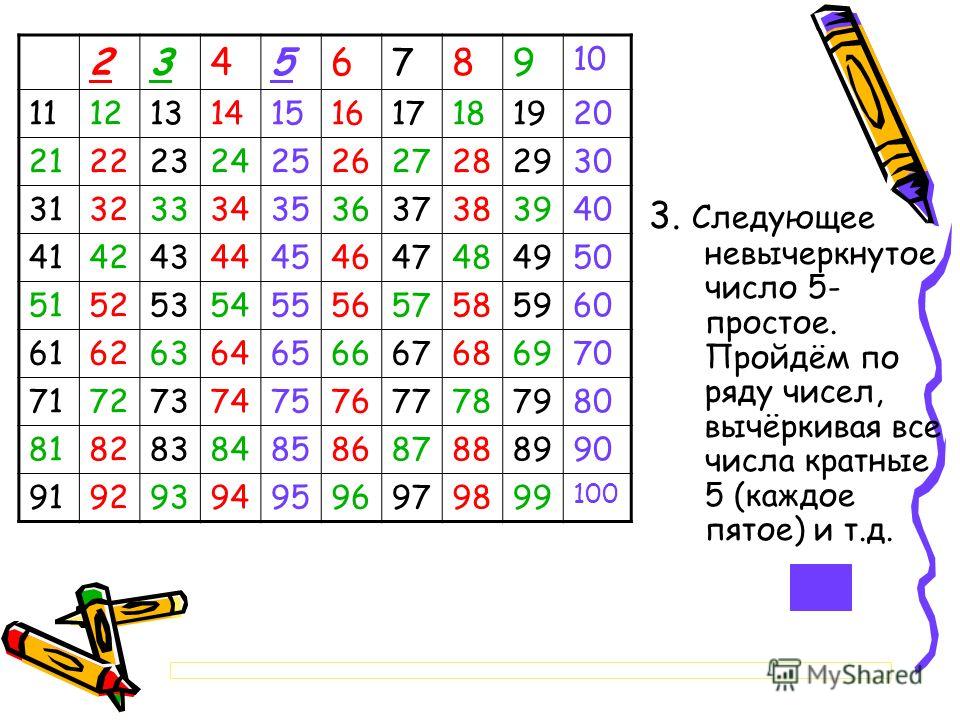 GIMPS предлагает исследовательские награды за открытие новых призовых чисел Мерсенна (Пейс выиграл 3000 долларов за свое недавнее открытие), в то время как Electronic Frontier Foundation предлагает ряд открытых задач для тех, кто первым обнаружил простые числа постоянно растущей величины. По оценкам GIMPS, потребуется 15 лет вычислений, чтобы достичь следующей вехи и найти простое число, состоящее не менее чем из 100 миллионов цифр.

Мотивация премии, учрежденной в 1990-х годах, необычна в современном контексте, говорит Сет Шоен из Electronic Frontier Foundation. «Награды призваны показать, насколько полезен Интернет — дать возможность людям, которые, возможно, никогда не встречались, работать вместе в больших масштабах для достижения целей», — пишет он в электронном письме.

И это сотрудничество является ключом к нахождению этих больших простых чисел. «Один человек с лопатой может найти большой драгоценный камень, но это очень маловероятно», — пишет Колдуэлл.