Простые и составные числа 6 класс онлайн-подготовка на Ростелеком Лицей
Игра
Рассмотрим рисунок 1, на нем выписан натуральный ряд чисел.
Рис. 1. Числа от 1 до 100 (Источник)
Правила игры
1. Берем число, а потом вычеркиваем все числа, которые на него делятся. Начинаем с 2.
Так, каждое второе число будет делиться на два (рис. 2).
Рис. 2. Вычеркивание всех чисел, которые делятся на 2
2. Берем следующее незачеркнутое число и обводим его кружочком. Вычеркиваем числа, которые делятся на три.
Рис. 3. Вычеркивание чисел, которые делятся на 3
3. Следующее незачеркнутое число – пять. Вычеркиваем все числа, делящиеся на пять (рис. 4).
Рис. 4. Вычеркивание чисел, которые делятся на 5
4. Берем число семь и продолжаем зачеркивать числа (рис. 5).
Рис. 5. Вычеркивание чисел, которые делятся на 7
5. Посмотрим, что получилось: зачеркнуты почти все числа. После того как мы подумаем над тем, что объединяет все зачеркнутые числа, ответим: они все на что-то делились. Те числа, которые остались незачеркнутыми (рис. 4), ни на что, кроме себя и единицы, не делятся.
Те числа, которые остались незачеркнутыми (рис. 4), ни на что, кроме себя и единицы, не делятся.
Данное действие называется решето Эратосфена – просеивание натурального ряда в поисках простых чисел. Простые числа – это такие числа, которые делятся на себя и на единицу (например: 2, 3, 5, 7 и т. д.). Те числа, которые делятся не только на себя и на единицу, имеют больше двух делителей, называются составными.
Есть интересное число, которое делится только на себя (имеет один делитель). Это единица, она не является ни простым, ни составным.
Группы натуральных чисел
Все натуральные числа – числа, которые мы используем при счете, можно разделить на три группы.
1. Простые – имеют только два делителя: единицу и само себя, например: 2, 3, 5, 7, 11, 17, 19, 23 и т. д.
2. Составные числа – имеют больше двух делителей, например: 4, 6, 8,10,15, 22 и т. д.
д.
3. Единица (1) имеет только один делитель.
Простые числа
Если посмотрим на таблицу простых чисел (рис. 6), то заметим, что все числа, кроме двойки, нечетные. Самое маленькое простое число – два. А самое большое из ныне найденных простых чисел содержит семнадцать миллионов четыреста двадцать пять тысяч сто семьдесят цифр: 17 425 170 цифр.
Рис. 6. Таблица некоторых простых чисел (Источник)
Основная теорема арифметики
Любое натуральное число можно разложить в произведение простых чисел единственным образом с точностью до порядка сомножителей.
1. Например, число 6 можно получить, если 3 умножить на 2 или 2 умножить на 3.
2. Аналогично раскладываем на простые множители число 48.
Обратите внимание: каждый раз мы выделяли простой множитель, а потом второй множитель раскладывали на множители и так, пока не получили все простые.
3. Теперь для разложения с помощью основной теоремы арифметики возьмем 122. Данное число делится на два, получаем 61. Так как шестьдесят один – это простое число, то разложение числа 122 на простые множители:
Теперь для разложения с помощью основной теоремы арифметики возьмем 122. Данное число делится на два, получаем 61. Так как шестьдесят один – это простое число, то разложение числа 122 на простые множители:
4. Если разложим число 462 на простые множители, получим:
В простых числах интересно то, что иногда они стоят через один (подряд простые числа стоять не могут, потому что каждое второе делится на 2, исключением является пара 2 и 3), например 3 и 5 или 71 и 73, или 461 и 463, такие числа называют «близнецами». Иногда простые числа очень далеко расположены друг от друга и найти каждое следующее простое число с каждым разом все сложнее.
Определение
Криптограф – специалист по расшифровке и зашифровыванию информации.
Так, криптографы используют большие простые числа, для того чтобы создавать коды, которые очень сложно взламывать.
В последующих уроках нам потребуются знания о простых числах, чтобы вычислять НОД – наибольший общий делитель и НОК – наименьшее общее кратное.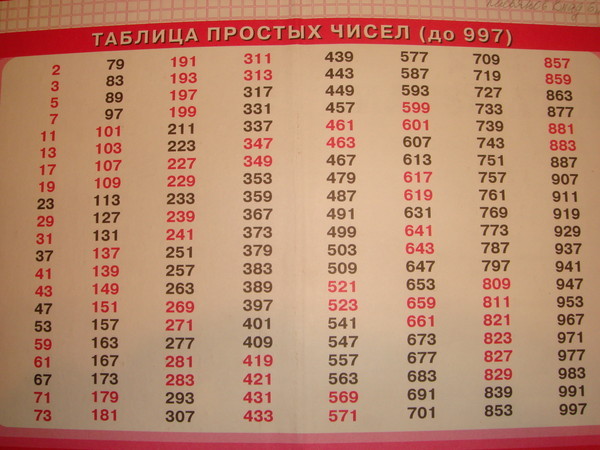
Список литературы
1. Математика. 6 класс. Учеб. для общеобразоват. учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – 30-е изд., стер. – М.: Мнемозина, 2013. – 288 с.: ил.
2. Зубарева И.И., Мордкович А.Г. Математика, 6 класс. – М.: Мнемозина.
3. Истомина Н.Б., Математика, 6 класс. – М.: Ассоциация ХХI век.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет портал «Научная библиотека» (Источник)
2. Интернет портал «Clever Students» (Источник)
3. Интернет портал «Школьный помощник» (Источник)
Домашнее задание
1. Математика. 6 класс. Учеб. для общеобразоват. учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – 30-е изд., стер. – М.: Мнемозина, 2013., ст. 17 § 4, № 95, 98, 104.
2. Что такое натуральные числа?
3. Какие группы натуральных чисел вы знаете?
4.*Разложите на простые множитель такие числа, воспользовавшись основной теоремой арифметики:
а) 335 б) 892 в) 647 г) 995 д) 44 е) 220
Найдено новое простое число длиной в 9,4 миллиона цифр | Futurist
Автор: Кира Константинова |
28 ноября 2016, 17:47
Международная группа ученых обнаружила новое простое число (имеет только два делителя – единицу и само себя) длиной в 9,4 миллиона цифр. Оно является седьмым по величине из самых больших простых чисел и сокращает количество кандидатов на число Серпинского до пяти.
Оно является седьмым по величине из самых больших простых чисел и сокращает количество кандидатов на число Серпинского до пяти.
Придуманная польским математиком Вацлавом Серпинским в 1960-х годах задача Серпинского просит найти наименьшее возможное число, соответствующее определенному сложному набору критериев. Число Серпинского должно быть положительным, нечетным, и занимать место K в формуле К*2n+1, в которой все числа являются составными (то есть не простыми). Другими словами, если K является числом Серпинского, все составляющие формулы К*2n+1 являются составными. Однако, чтобы доказать, что K является числом Серпинского, нужно показать, что К*2n+1 является составным для каждого n. Если n – простое число, ничего не получится.
На сегодня самое маленькое известное число Серпинского – 78557, предложенное американским математиком Джоном Селфриджем еще в 1962 году.
За последние 50 лет математики нашли шесть возможных кандидатов: 10223, 21181, 22699, 24737, 55459 и 67607. Но до сих пор никто не смог доказать, что любое из них точно является числом Серпинского. Для этого необходимо предоставить математическое доказательство того, что, каким бы ни было n, К*2n+1 никогда не станет простым числом. Поэтому важно узнать как можно больше простых чисел. В этом помогает проект Seventeen or Bust.
Но до сих пор никто не смог доказать, что любое из них точно является числом Серпинского. Для этого необходимо предоставить математическое доказательство того, что, каким бы ни было n, К*2n+1 никогда не станет простым числом. Поэтому важно узнать как можно больше простых чисел. В этом помогает проект Seventeen or Bust.
Его участники загружают специальное ПО на свой компьютер и сообща ищут новые простые числа. Так и было найдено последнее простое число длиной в 9 383 761 цифру (оно равно 10223*231172165+1). Тысячи компьютеров объединенной командой искали это число в течение восьми дней.
Таким образом, если 10223*231172165+1 – простое, то 10223 исключается из списка кандидатов на число Серпинского и их остается только пять.
Самое большое известное простое число было открыто в январе 2016 года и в нем 22 миллиона цифр. Вот как оно выглядит на бумаге:
Подпишись на еженедельную рассылку
Теги
числа
математика
число Серпинского
Фото: informys.ru
Что такое простое число? Объяснение для учителей, родителей и детей
Простое число — это число, которое можно разделить только само на себя и на 1 без остатка. Здесь мы подробно объясним, что это значит, дадим вам список простых чисел, которые дети должны знать в начальной и средней школе, и предоставим вам несколько практических вопросов и примеров.
Что такое простое число?
Простое число — это целое число больше 1, имеющее только два делителя — само себя и 1.
Простое число нельзя разделить ни на какие другие положительные целые числа без остатка, десятичной дроби или дроби.
Примером простого числа является 13. Его делителями являются только 1 и 13. При делении простого числа на другое натуральное число остаются числа. Например, 13 ÷ 6 = 2, остаток 1.
15 не является примером простого числа, потому что оно может делиться на 5 и 3, а также само по себе, а 1.
15 является примером составного числа. число, потому что оно имеет более двух делителей.
Простые числа часто рассматриваются математиками в качестве «кирпичиков» в теории чисел. Основная теорема арифметики гласит, что составное число можно представить в виде произведения простых чисел.
См. также: Правила делимости
Рабочие листы с простыми числами
Бесплатно загружаемый рабочий лист с простыми числами включает практические вопросы и ключ ответа
Примеры простых чисел
Как определить, является ли заданное число простым или составным число, основанное на свойствах простых чисел.
Что такое простые числа?
- Есть 8 простых чисел меньше 20: 2, 3, 5, 7, 11, 13, 17 и 19.
- Первые 10 простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.
- Существует 25 простых чисел от 1 до 100.
- Простые числа включают большие числа и могут продолжаться далеко за пределы 100.
- Например, 21 577 — простое число.
Список простых чисел до 100
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97
Обратите внимание, что этот список простых чисел содержит только нечетные числа, с исключение числа 2.
Наименьшее простое число
2 — наименьшее простое число. Кроме того, это единственное четное простое число — все остальные четные числа могут делиться как минимум сами на себя, на 1 и 2, то есть у них будет как минимум 3 делителя.
Наибольшее простое число
Греческий математик Евклид (один из самых известных математиков классической эпохи) записал доказательство того, что среди множества простых чисел нет наибольшего простого числа. Тем не менее, многие ученые и математики все еще пытаются найти его в рамках Великого Интернет-поиска простых чисел Мерсенна.
Тем не менее, многие ученые и математики все еще пытаются найти его в рамках Великого Интернет-поиска простых чисел Мерсенна.
наибольшее известное простое число (по состоянию на ноябрь 2020 г.) равно 2 82 589 933 − 1, число, состоящее из 24 862 048 цифр при записи по основанию 10. , имеющий 23 249 425 цифр.
К тому времени, как вы это прочтете, он может стать еще больше, но вы можете следить за его развитием в Википедии.

Часто задаваемые вопросы о простых числах
Что такое простое число в математике?
Простое число — это число, которое можно разделить только на себя и на 1 без остатка.
Какие простые числа от 1 до 100?
Простые числа от 1 до 100: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Почему 1 не простое число?
1 не является простым числом, потому что оно имеет только один делитель, а именно 1. Простые числа должны иметь ровно два делителя.
Почему 2 простое число?
2 — простое число, потому что его единственными делителями являются 1 и оно само.
Является ли 51 простым числом?
51 не является простым числом, потому что оно имеет 3 и 17 в качестве делителей, а также само себя и 1. Другими словами, 51 имеет четыре делителя.
Рабочие листы с простыми числами
Бесплатно загружаемый рабочий лист с простыми числами включает практические вопросы и ключ ответа
Как простые числа используются в реальном мире?
Одним из наиболее важных применений простых чисел является кибербезопасность — обеспечение большей безопасности информации, передаваемой через Интернет.
Чтобы зашифровать (защитить) такие вещи, как данные кредитной карты, медицинские записи и даже некоторые службы обмена сообщениями, такие как WhatsApp, инженеры-программисты создают алгоритмы, используя простые числа.
Перемножая два очень больших простых числа (некоторые компании используют простые числа, состоящие из сотен цифр!), мы получаем еще большее число, исходные множители которого (два очень больших простых числа) известны только нам. Затем мы используем это еще большее число для шифрования нашей информации.
Если кто-то еще хочет узнать, какую информацию мы посылаем, он должен выяснить, каковы были наши первоначальные факторы. С такими длинными простыми числами, как те, которые мы использовали, им могут потребоваться годы или даже десятилетия постоянных проб и ошибок, прежде чем они найдут хотя бы одно. Такая криптография с открытым ключом обеспечивает безопасность нашей информации.
Хотите знать, как объяснить своим детям другие ключевые слова по математике? Ознакомьтесь с нашим словарем Primary Math Dictionary или попробуйте эти основные математические термины:
- Что такое число в кубе: объяснение для основных родителей и детей
- Что такое наименьшее общее кратное: объяснение для основных родителей и детей
- Что такое наивысший общий фактор: объяснение для основных родителей и детей
Вопросы о простых числах
1) Квадратное число и простое число имеют в сумме 22. Какие это два числа?
Какие это два числа?
A: 9 и 13
2) Эмма думает о двух простых числах. Она складывает два числа вместе. Ее ответ — 36. Напишите все возможные пары простых чисел, которые могла придумать Эмма.
А: 3 и 33; 5 и 31; 7 и 29; 13 и 23; 17 и 19
3) Обведите два простых числа – 29, 59, 39, 69, 29
A: 29 и 59
4) Запишите три простых числа, при умножении которых получается 231.
27 A: 3 x 7 x 11
ЗАДАЧА: Чен выбирает простое число. Он умножает его на 10, а затем округляет до ближайшей сотни. Его ответ — 400. Напишите все возможные простые числа, которые мог выбрать Чен.
A: 37, 41 или 43.
Онлайн-центр Third Space Learning Maths Hub содержит сотни математических ресурсов для учителей начальной школы и родителей, которые можно использовать в школе и дома. Регистрация на бесплатных математических ресурсах выполняется быстро, легко и доступна для всех сотрудников вашей школы. Чтобы получить доступ к премиум-ресурсам, вашей школе потребуется премиум-подписка Maths Hub. Кроме того, доступ ко всем ресурсам премиум-класса включен бесплатно для школ, подписавшихся на наше онлайн-обучение по математике.
Чтобы получить доступ к премиум-ресурсам, вашей школе потребуется премиум-подписка Maths Hub. Кроме того, доступ ко всем ресурсам премиум-класса включен бесплатно для школ, подписавшихся на наше онлайн-обучение по математике.
Рабочие листы с простыми числами
- Готовые уроки Умножение и деление 5 класса (осенний блок 4) Слайды и рабочие листы
- Готовые уроки 6 класс 4 Операции (Осенний блок 2) Слайды и рабочие листы
- Рабочий лист 5-го класса: умножение и деление 1
- Рабочий лист 6-го класса: четыре операции
Видео о простых числах
- Как учить простые и составные числа
Есть ли у вас ученики, которым нужна дополнительная помощь по математике?
Предоставьте своим учащимся четвертого и пятого классов больше возможностей для закрепления навыков обучения и практики с помощью персонализированного обучения элементарной математике с их собственным онлайн-репетитором по математике.
Каждый учащийся получает дифференцированное обучение, предназначенное для устранения индивидуальных пробелов в обучении, а организованное обучение гарантирует, что каждый учащийся учится в нужном темпе. Уроки соответствуют стандартам и оценкам вашего штата, плюс вы будете получать регулярные отчеты о каждом шаге.
Программы доступны для четвертого и пятого классов, и вы можете попробовать 6 уроков абсолютно бесплатно.
Содержание этой статьи изначально было написано учителем начальных классов Софи Бартлетт, а затем было отредактировано и адаптировано для школ США учителем математики начальных классов Кэти Китон.
Какое самое маленькое простое число? Четное ли это число…
Перейти к
- Игра с числами. Упражнение 2.1.
- Игра с числами. Упражнение 2.8.
- Игра с числами.
 Упражнение 2.2.
Упражнение 2.2. - Игра с числами. Упражнение 2.3.
- Игра с числами. Упражнение 2.4.
- Игра с числами. Упражнение 2.5.
- Игра с числами. Упражнение 2.6.
- Игра с числами. Упражнение 2.7.
- Игра с числами.
 Упражнение 2.9.
Упражнение 2.9. - Игра с числами. Упражнение 2.10.
- Игра с числами. Упражнение 2.11.
- Зная свои числа
- Игра с числами
- Целые числа
- Действия над целыми числами
- Отрицательное число и целые числа
- Фракции
- Десятичные
- Введение в алгебру
- Соотношение, пропорция и унитарный метод
- Основные геометрические понятия
- Углы
- Треугольники
- Круги
- Пара прямых и поперечная
- Понимание трехмерных форм
- Симметрия
- Основные геометрические инструменты
- Геометрические построения
- Измерение
- Обработка данных Представление данных
- Обработка данных – II
- Гистограммы обработки данных
Главная >
РД Шарма Решения
Класс 6
Математика
>
Глава 2. Игра с числами
Игра с числами
>
Игра с числами. Упражнение 2.3.
>
Вопрос 3
Вопрос 3 Игра с числами Упражнение 2.3
Какое самое маленькое простое число? Это четное число?
Ответ:
2 — наименьшее простое число.
Мы знаем, что 2 — четное простое число, поскольку оно делится на 2.
Похожие вопросы
Что такое простые числа? Перечислите все простые числа от 1 до 30.
Запишите все простые числа между: (i) 10 и 50 (ii) 70 и 90 (iii) 40 и 85 (iv) 60 и 100
Какое наименьшее нечетное простое число? Всякое ли нечетное число является простым числом? Если нет, то приведите пример ода…
Что такое составные числа? Может ли составное число быть нечетным? Если да, напишите наименьшее нечетное составное. ..
..
Что такое простые числа-близнецы? Запишите все пары простых чисел-близнецов от 50 до 100.
Что такое со-премьеры? Приведите примеры пяти пар взаимно простых чисел. Всегда ли взаимные простые числа являются простыми? Если нет, то рис…
Фейсбук
Копировать ссылку
Было ли это полезно?
Упражнения
Игра с числами Упражнение 2.1
Игра с числами Упражнение 2.8
Игра с числами Упражнение 2.2
Игра с числами Упражнение 2.3
игра с номерами Упражнение 2.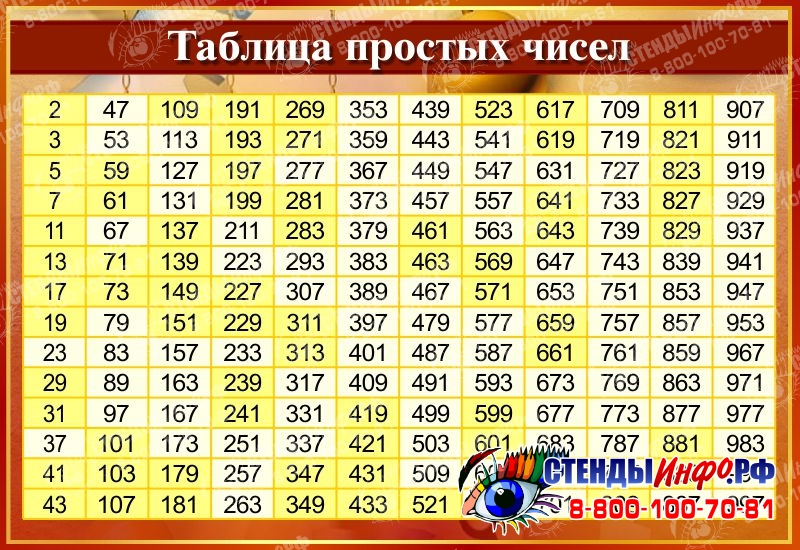

 Упражнение 2.2.
Упражнение 2.2. Упражнение 2.9.
Упражнение 2.9.