Шарообразная земля: как древние греки придумали географию |

Содержание

история открытия – Мир Знаний

У каждого народа формировались собственные представления о том, что представляет собой наша планета. Например, вавилоняне в VI тысячелетии до н. э. были убеждены: Земля — это одна большая гора, окруженная морем, на котором лежит небесная твердь; Солнце вечером прячется под землю и за ночь проходит путь с запада на восток, а утром поднимается на небо и катится в западном направлении по островкам суши — зодиакальным созвездиям, расположенным среди небесного моря.

Между тем китайцы, у которых искусство рисовать карты возникло еще за 1000 лет до н. э., не сомневались, что Земля прямоугольная и плоская, а небо над ней похоже на купол и держится на четырех колоннах. Пятую колонну, установленную посередине, сбил свирепый дракон, поэтому земля накренилась на восток, а небесная сфера — к западу, и все небесные тела устремились именно туда.

Индусы воображали Землю в виде громадной тарелки, покоящейся на слоновьих спинах.

В VII—VI вв. до н. э. древнегреческие мыслители Фалес Милетский, Анаксимандр и Анаксагор представляли, будто все человечество обитает то ли на гигантском пеньке, то ли на доске, то ли на обрубке дерева, которые покачиваются на морских волнах либо парят на подушке из сжатого воздуха. Собственно, на мысли о плоской планете их натолкнули знаменитые классические поэмы «Одиссея» Гомера и «Теогония» Гесиода, поэтому не удивительно, что описанная там картина мира надолго укоренилась в сознании людей.

Прошло два, три, четыре столетия, а серьезные натурфилософы, которые заложили основы учения о том, что вся материя состоит из микроскопических частиц-атомов, и слышали (в частности, от Аристотеля) гипотезы о шарообразности Земли, пытались доказать обратное. Скажем, Демокрит — автор идей бесконечности Вселенной и ее возникновения вследствие столкновений атомов — уверял: будь Земля круглой, Солнце по вечерам пряталось бы за дуговой, а не ровный горизонт. А Эпикур, который экспериментально изучал природу молний, ветров, землетрясений и пр. , считал, тем не менее, что атомы падают на плоскую Землю из Космоса, словно снежинки, и так же, кружась, склеиваются между собой в разные крупные тела.

Среди христиан подобные воззрения бытовали вплоть до XVI века. К примеру, византийский купец Козьма Индикоплов в своей «Христианской топографии» описал Вселенную как сундук, внутри которого прячется прямоугольник тверди с горой на севере и морем вокруг. А в сборнике славянских духовных стихов «Голубиная книга» изложена легенда о китах, на которых держится весь мир.

Впрочем, знаменитый греческий математик Пифагор, который жил в VI—V вв. до н. э., за два столетия до Аристотеля, уже догадывался, что наша планета далеко не плоская, а с ним этими знаниями поделился моряк Скилак Кариандский. Аристотель же последовательно доказал предположения Пифагора: уходя за горизонт, суда не уменьшаются постепенно, а словно «проваливаются»; во время лунных затмений Земля отбрасывает на спутник круглую тень; в разных частях света люди видят не одни и те же звезды, то есть светила заслоняются Землей.

Последователю Аристотеля, Эратосфену, даже удалось определить радиус земного шара с погрешностью всего 1 %. Используя скафис — примитивный прибор для измерения углов, состоящий из шеста-гномона и чаши с делениями, — ученый сравнил положение Солнца в одно и то же время в северном египетском городе Александрия и в южной Сиене. На юге ровно в полдень гномон не отбрасывал тени (солнце стояло в зените), а на севере тень от шеста упала на чашу, показав 7,2-градусное отклонение от зенита. Эратосфен знал, что расстояние между двумя городами составляет 800 км, и на этом основании составил формулу: приравнял отношение полного угла (360°) и полученного (7,2°) к отношению неизвестной длины земной окружности и участка в 800 км. Расчеты показали, что экватор Земли простирается на 40 000 км, и, чтобы найти радиус, ученый разделил это число на удвоенное число пи, получив в итоге 6371 км.

Примерно в то же время греческий астроном Аристарх Самосский создал модель Солнечной системы, в которой Земля вращалась вокруг неподвижного Солнца и вокруг собственной оси. Согласно с традиционными взглядами, Аристарх воображал Вселенную заключенной в сферу с прикрепленными к ней звездами, но эта сфера, по его мнению, была практически безграничной. В том, что Земля не только похожа на шар, но и вращается вокруг своей оси, в 1520-х на горьком опыте убедилась команда путешественника Фернана Магеллана. Плывя на запад, моряки за четыре года обогнули всю Землю, но домой вернулись на день позже, чем рассчитывали: из-за того что планета крутится с запада на восток, корабли Магеллана постоянно притормаживали.

В том же XVI в. идею Аристарха на научном уровне поддержал польский астроном Николай Коперник (1473—1543) — в первой версии его знаменитого труда «Об обращении небесных сфер» даже было признание в том, что автор просто развил теорию великого грека.

В XVIII в. человечество заподозрило, что Земля не идеально круглая, а сплюснутая, только вот где — на полюсах или на экваторе, — не знал никто. Чтобы выяснить это, французы отправили в Перу и в приполярную зону две научные экспедиции, которые должны были провести разнообразные измерения местности и видимого небосвода. В результате выяснилось, что 1° меридиана (1/360 линии пересечения Земли с плоскостью, проходящей через ось вращения) на полюсе меньше, чем на экваторе — 110,6 против 111,9 км. Это могло означать одно: планету словно сжали сверху и снизу гигантскими ладонями, превратив в сфероид (вращающийся эллипс).

Кстати, пока французские ученые проводили полевые исследования, английский физик Исаак Ньютон (1643—1727) поставил воображаемый опыт: мысленно «прокопал» тоннели к центру Земли от экватора и от полюса, залил туда воды и «увидел», что экваториальную воду как бы выталкивает центробежная сила, направленная от центра планеты наружу перпендикулярно оси. Значит, заключил ученый, экваториальный тоннель должен быть длиннее полярного, дабы уравновесить жидкости. И чем быстрее крутится какое-либо тело, тем сильнее его сожмет. Впрочем, позже астрофизики выяснили, что всяческие перепады высот грунта и океанического дна делают Землю не идеально эллиптической, а несколько неровной. Эта форма была названа геоидом.

Что интересно, представители разных религий долгое время не могли смириться с идеей неплоской Земли (хотя, вопреки расхожему мнению, и не преследовали адептов «объемной» теории). В конце XIX в. в Англии даже было основано Общество плоской Земли, которое существовало вплоть до начала нашего столетия и с середины ХХ в. включало около 3000 членов. Все они свято верили в то, что астрономические наблюдения — ложь, для чего-то необходимая властям, а фотографии из космоса — наглая подделка.

Наш канал в Телеграм

«Как выглядит самый простой и неопровержимый аргумент, подтверждающий, что Земля—шарообразная, а не плоская?» — Яндекс Кью

Юрий Лоза предъявил доказательства того, что Земля плоская

https://ria.ru/20200918/zemlya-1577433974.html

Юрий Лоза предъявил доказательства того, что Земля плоская

Юрий Лоза предъявил доказательства того, что Земля плоская — РИА Новости, 18.09.2020

Юрий Лоза предъявил доказательства того, что Земля плоская

Певец и композитор Юрий Лоза поделился с “Пятым каналом” четырьмя аргументами в пользу теории о плоской Земле. По словам исполнителя, основные доводы он… РИА Новости, 18.09.2020

2020-09-18T12:12

2020-09-18T12:13

юрий лоза

/html/head/meta[@name=’og:title’]/@content

/html/head/meta[@name=’og:description’]/@content

https://cdnn21. img.ria.ru/images/07e4/09/11/1577384281_0:0:2932:1649_1920x0_80_0_0_4811ed9d146988cff531256658056c83.jpg

МОСКВА, 18 сен — РИА Новости. Певец и композитор Юрий Лоза поделился с “Пятым каналом” четырьмя аргументами в пользу теории о плоской Земле. По словам исполнителя, основные доводы он почерпнул из книги Эрика Дюбэй «200 доказательств того, что Земля не шар», а остальные — из собственного опыта и от родственников — летчиков и мореходов.Певец сообщил, что во время учебы на географическом факультете в Казахском государственном университете он узнал о том, что у геодезистов нет понятия о шарообразной Земле. Также, по словам музыканта, мореходы не пользуются глобусом. Об этом артисту поведал его тесть-моряк. «Ни в одной компании не стоит глобус. Ни один капитан в мире не рассчитывает свой маршрут, какие-то там по фарватеру свои движения по глобусу — только по картам плоской Земли. Потому что если плыть по глобусу, то поплывешь неизвестно куда», — добавил певец. Следующий аргумент Лоза узнал от дяди, который прослужил в авиации 30 лет. Согласно ему, самолеты летают только по прямой плоскости и только в северном полушарии, “как будто летят по плоской Земле”. Кроме этого, еще одним доказательством музыкант считает тот факт, что на всех новейших навигационных интернет-ресурсах нет перемещений самолетов и кораблей в Южном полушарии.Последний аргумент в пользу теории о плоской Земле — климат на полюсах, считает Юрий Лоза. Как отметил музыкант, если бы Земля имела шарообразную форму, среднегодовая температура на Северном и Южном полюсах не могла бы отличаться на 20 градусов.

https://ria.ru/20200916/kosmos-1577340879.html

РИА Новости

4.7

[email protected]

7 495 645-6601

ФГУП МИА «Россия сегодня»

https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/

2020

РИА Новости

4.7

[email protected]

7 495 645-6601

ФГУП МИА «Россия сегодня»

https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/

Новости

ru-RU

https://ria. ru/docs/about/copyright.html

https://xn--c1acbl2abdlkab1og.xn--p1ai/

РИА Новости

4.7

[email protected]

7 495 645-6601

ФГУП МИА «Россия сегодня»

https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/

1920

1080

true

1920

1440

true

https://cdnn21.img.ria.ru/images/07e4/09/11/1577384281_203:0:2932:2047_1920x0_80_0_0_3d95dca248df93216034a4cadf5f1082.jpg

1920

true

РИА Новости

4.7

[email protected]

7 495 645-6601

ФГУП МИА «Россия сегодня»

https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/

РИА Новости

4.7

[email protected]

7 495 645-6601

ФГУП МИА «Россия сегодня»

https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/

юрий лоза

Юрий Лоза

МОСКВА, 18 сен — РИА Новости. Певец и композитор Юрий Лоза поделился с “Пятым каналом” четырьмя аргументами в пользу теории о плоской Земле. По словам исполнителя, основные доводы он почерпнул из книги Эрика Дюбэй «200 доказательств того, что Земля не шар», а остальные — из собственного опыта и от родственников — летчиков и мореходов.

Певец сообщил, что во время учебы на географическом факультете в Казахском государственном университете он узнал о том, что у геодезистов нет понятия о шарообразной Земле.

«Все эти формулы геодезические, когда вы берете из какой-то точки снимаете показания какие-то, по формуле вычисляете расстояние, и никто не берет поправки на круглую Землю», — цитирует слова Лозы “Пятый канал”.

Также, по словам музыканта, мореходы не пользуются глобусом. Об этом артисту поведал его тесть-моряк. «Ни в одной компании не стоит глобус. Ни один капитан в мире не рассчитывает свой маршрут, какие-то там по фарватеру свои движения по глобусу — только по картам плоской Земли. Потому что если плыть по глобусу, то поплывешь неизвестно куда», — добавил певец.

16 сентября 2020, 18:23Хочу стать космонавтом

Российский космонавт поспорил со сторонниками теории плоской Земли

Следующий аргумент Лоза узнал от дяди, который прослужил в авиации 30 лет. Согласно ему, самолеты летают только по прямой плоскости и только в северном полушарии, “как будто летят по плоской Земле”. Кроме этого, еще одним доказательством музыкант считает тот факт, что на всех новейших навигационных интернет-ресурсах нет перемещений самолетов и кораблей в Южном полушарии.

Последний аргумент в пользу теории о плоской Земле — климат на полюсах, считает Юрий Лоза. Как отметил музыкант, если бы Земля имела шарообразную форму, среднегодовая температура на Северном и Южном полюсах не могла бы отличаться на 20 градусов.

2.4 Почти сферическая Земля

Вы знаете, что Земля не плоская; но, как мы уже поняли, он и не сферический! Для многих целей мы можем игнорировать отклонение от сферы; но, если точность имеет значение, Землю лучше всего описать как геоид.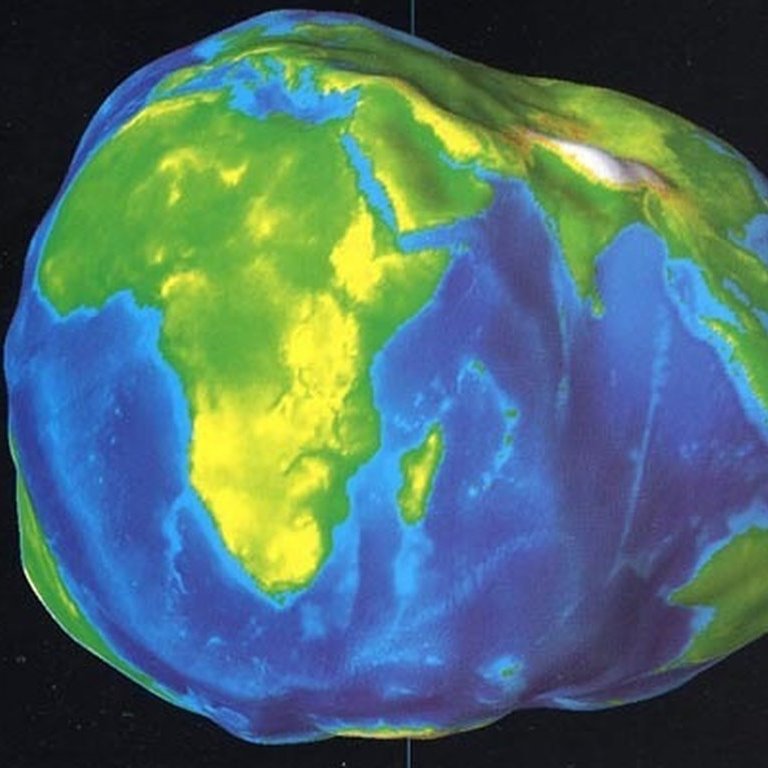 Геоид — эквипотенциальная поверхность гравитационного поля Земли; проще говоря, он имеет форму комковатого, слегка сплющенного шара. Определение точной формы геоида является главной задачей науки геодезия, изучение размеров, формы Земли, гравитационных и магнитных полей. Точность координат, определяющих географические местоположения, зависит от того, как сетка системы координат совмещена с поверхностью Земли, и это совмещение зависит от модели, которую мы используем для представления фактической формы геоида. Хотя геодезия — старая наука, остается много сложных проблем, и геодезисты продолжают добиваться успехов, которые увеличивают нашу способность точно определять местонахождение (и постепенно делают местоположение GPS в вашем телефоне более точным).

Геоиды неровные, потому что гравитация меняется от места к месту в ответ на местные различия в рельефе и различия в плотности материалов в недрах Земли. Геоид Земли также немного приземистый, как предполагалось выше. Сила тяжести на уровне моря на полюсах больше, чем сила тяжести на уровне моря на экваторе, что является следствием «сплюснутой» формы Земли, а также центробежной силы, связанной с ее вращением.

Рисунок 2.23. Форма Земли определяется как поверхность, близко близкая к среднему глобальному уровню моря, но на которой гравитация везде одинакова. Карикатура геоида, показанная выше, нарисована не в масштабе; нарушения сильно преувеличены.

Авторы и права: из Scales and Transformations Дэвида ДиБиасе, под лицензией CC BY-NC-SA 4.0

Геодезисты Национальной геодезической службы США (NGS Geoid 12A) описывают геоид как «эквипотенциальную поверхность», поскольку связанная с ней потенциальная энергия с гравитационным притяжением Земли эквивалентна везде на поверхности. Геоид — это, по сути, трехмерная математическая поверхность, которая (насколько это возможно) соответствует гравитационным измерениям, проведенным в миллионах мест по всему миру. По мере появления дополнительных и более точных измерений силы тяжести геодезисты периодически пересматривают форму геоида. Некоторые модели геоида решаются только для ограниченных областей; Например, GEOID03 рассчитывается только для континентальной части США 9.0007

Важно отличать неровности геоида от неровностей рельефа Земли, поскольку геоиды зависят от гравитационных измерений, а не просто представляют топографические особенности Земли. Хотя топография Земли состоит из экстремальных высот, таких как гора Эверест (29 029 футов над уровнем моря), и невероятных глубин, таких как Марианская впадина (36 069 футов ниже уровня моря), в среднем рельеф Земли относительно ровный. Астроном Нил де Грасс Тайсон (2009) отмечает: «Земля как космический объект удивительно гладкая; если бы вы взяли гигантский палец и провели им по поверхности Земли (океанам и всему остальному), Земля была бы такой же гладкой, как биток. Дорогие глобусы, на которых изображены приподнятые участки земной суши, указывающие на горные хребты, изображают сильно преувеличенную реальность (стр. 39).).»

2.4.1 Эллипсоид

Эллипсоид представляет собой трехмерную геометрическую фигуру, напоминающую сферу, но экваториальная ось которой ( a на рис. 2.23 выше) немного длиннее, чем ее полярная ось ( b ).Эллипсоиды обычно используются в качестве заменителей геоидов для упрощения математических расчетов, используемых для связывания сетки системы координат с моделью формы Земли. реальной формы Земли, чем простая сфера. Одно из следствий различных моделей Земли состоит в том, что они представляют высоты мест как разные. Геодезисты и инженеры измеряют высоты на строительных площадках и в других местах. Высоты выражаются по отношению к вертикальная отметка , опорная поверхность, такая как средний уровень моря. Различные геоиды и разные эллипсоиды определяют вертикальную датум по-разному. На приведенной ниже карте (рис. 2.24) показаны различия высот между моделью геоида GEOID96 и эллипсоидом WGS84. Поверхность GEOID96 представляет собой поверхность на 75 метров выше, чем эллипсоид WGS84 над Новой Гвинеей (где карта окрашена в красный цвет). В Индийском океане (где карта окрашена в фиолетовый цвет) поверхность GEOID96 представляет собой поверхность примерно на 104 метра ниже поверхности эллипсоида.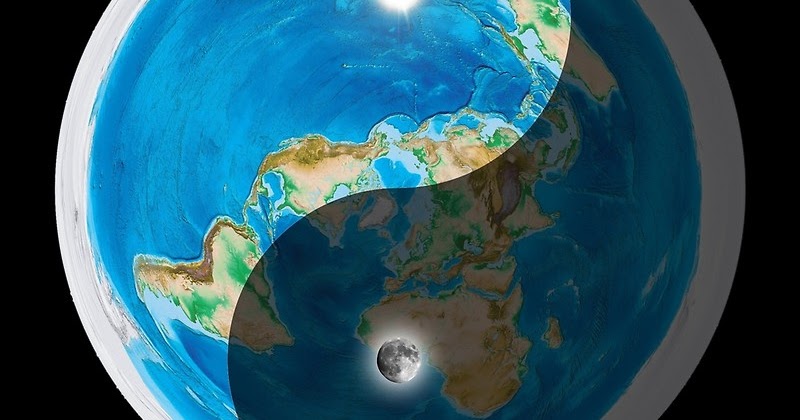

Многие эллипсоиды используются по всему миру. Локальные эллипсоиды минимизируют различия между геоидом и эллипсоидом для отдельных стран или континентов. Эллипсоид Clarke 1866, например, минимизирует отклонения в Северной Америке.

Рисунок 2.24. Отклонения между эллипсоидом и геоидом.

Авторы и права: Национальная геодезическая служба, 1997 г.

После того, как мы определили предпочтительную форму для представления Земли (конкретный эллипсоид), следующим вопросом, который мы должны рассмотреть, является система координат, чтобы обеспечить средства для определения положения местоположения на этой сфере (сферическая система координат).

2.4.2 Горизонтальные исходные данные

Горизонтальные исходные данные — неуловимое понятие для многих специалистов по ГИС. Однако это относительно легко понять, если мы начнем с концепции, что данные определяют положение системы координат по отношению к размещаемым местам. Прежде чем рассматривать горизонтальные датумы в контексте географических (сферических) координат, рассмотрим приведенный ниже простой пример, в котором используются плоские координаты. В этом примере «датум» — это простая декартова сетка. На рисунке показано, что произошло бы, если бы горизонтальная система отсчета любой плоской системы координат имела бы другое начало, из которого были определены все координаты (например, если бы ложное начало любой зоны SPCS было немного другим местом).0007

Рисунок 2.25. Рисунки, показывающие смещение положения точки из-за изменения датума. Основываясь на оранжевой сетке, местоположение в Государственном колледже, штат Пенсильвания, обозначенное черной точкой, имеет координаты X и Y, соответственно, 3,0, 3,0. Если используемая «исходная точка» определяется оранжевой сеткой, начало которой (точка 0-0) немного севернее и восточнее фиолетовой сетки, та же точка в Государственном колледже имеет расположение 2,5, 2,5. . Место в мире не изменилось, но оно имеет другие координаты, потому что данные, используемые для определения координатного пространства, сместились.

Авторы и права: Rachael Bianchetti, © Penn State University, лицензия CC BY-NC-SA 4. 0

Исходя из приведенной выше модели, относительно легко визуализировать горизонтальную датум в контексте неспроецированных географических координат по отношению к опорный эллипсоид. Просто наложите сетку широты и долготы на эллипсоид и сдвиньте ее, чтобы правильно выровнять координаты с эллипсоидом, и вот ваш горизонтальный датум. Однако сложнее думать об датуме в контексте координатной сетки проекции, такой как UTM и SPC. Подумайте об этом так: сначала наложите сетку широты и долготы на эллипсоид. Затем спроецируйте эту сетку на двумерную плоскую поверхность. Наконец, наложите прямоугольную сетку восточного и северного направлений на проекцию, используя контрольные точки для географической регистрации сетки. Вот вам и спроецированная координатная сетка, основанная на горизонтальной системе отсчета. Это будет выглядеть так же, как в примере выше; разница в том, как мы выясняем соответствие между сеткой и миром.

Во всем мире геодезисты определяют различные горизонтальные данные, которые подходят (точно) для разных мест. Датумы периодически обновляются, поскольку технология позволяет повысить точность, но изменения происходят нечасто, поскольку каждый раз, когда вносятся изменения, возникают серьезные последствия (в плане затрат и времени) для обновления информации о местоположении для каждого места, к которому относится датум. В США двумя наиболее часто встречающимися горизонтальными датумами являются Североамериканский датум 1927 (NAD 27) и данные по Северной Америке 1983 года (NAD 83). Появление Глобальной системы позиционирования (GPS) потребовало обновления NAD 27 до NAD 83, которое включало (а) принятие геоцентрического эллипсоида GRS 80 вместо эллипсоида Кларка 1866 года; и (б) исправление многих искажений, которые накопились в более старых данных. Принимая во внимание, что реализация базы представляет собой сеть местоположений фиксированных контрольных точек, которые были заданы относительно одной и той же базовой поверхности, 1983 корректировка североамериканского датума привела к изменению значений координат каждой контрольной точки, управляемой Национальной геодезической службой (NGS). Очевидно, что сами точки не сместились из-за трансформации датума (хотя они смещались на сантиметр или более в год из-за тектоники плит). Скорее, сетки системы координат, основанные на системе отсчета, сместились относительно нового эллипсоида (точно так же, как сдвиг в координатах на плоскости, показанный выше), и поскольку локальные искажения были скорректированы одновременно, величина смещения сетки варьируется от места к месту. . На приведенном ниже рисунке сравнивается величина смещения сетки, связанная с регулировкой NAD 83 в одном месте.

Рисунок 2.26. Величина смещения сетки, связанная с регулировкой NAD 83 в одном месте.

Авторы и права: Геологическая служба США, общественное достояние. используйте для корректировки локальных данных на основе более старых данных. Вместо этого NGS создала программу под названием NADCON (Dewhurst 19).90, Mulcare 2004), который вычисляет скорректированные координаты из заданных пользователем входных координат путем интерполяции пары сеток коррекции 15°, созданных NGS из сотен тысяч ранее скорректированных контрольных точек. Национальная геодезическая служба США (NGS Geoid Home) ведет базу данных спецификаций координат этих контрольных точек, включая исторические местоположения, а также более поздние корректировки.

Рисунок 2.27. Горизонтальная контрольная точка.

Авторы и права: Национальная геодезическая служба, 2004 г.

Геоиды, эллипсоиды и даже системы координат — все это абстракции. Тот факт, что «горизонтальные данные» относятся к отношениям между эллипсоидом и системой координат, двумя абстракциями, может объяснить, почему это понятие так часто неправильно понимают. Датумы имеют физические проявления: около двух миллионов горизонтальных и вертикальных контрольных точек, установленных в США. Хотя маркеры контрольных точек фиксированы, координаты, определяющие их местоположение, могут меняться. В США расположение горизонтальных контрольных точек высокого порядка отмечено постоянными металлическими «памятниками», подобными показанному выше на рис. 2.27. Физическое воплощение данных представляет собой сеть измерений опорных точек, которые в реальном мире отмечены этими памятниками (Национальная геодезическая служба, 2004 г. ).

Практическая викторина

Зарегистрированные учащиеся штата Пенсильвания должны вернуться сейчас – пройти тест для самооценки по теме «Почти сферическая Земля» .

Вы можете проходить пробные тесты столько раз, сколько пожелаете. Они не оцениваются и никак не влияют на вашу оценку.

Косейсмическая деформация от землетрясения, разлома слоистой сферической Земли | Международный геофизический журнал

Журнальная статья

Фред Ф. Поллитц

Ищите другие работы этого автора на:

Оксфордский академический

Google ученый

ОБЪЯВЛЕНИЯ

Geophysical Journal International , том 125, выпуск 1, апрель 1996 г., страницы 1–14, https://doi.org/10.1111/j.1365-246X.1996.tb06530.x

Опубликовано:

01 Апрель 1996 г.

История статьи

Получено:

18 сентября 1995 г.

Принято:

21 сентября 1995 г.

Опубликовано:

01 апреля 1996 г.

Фильтр поиска панели навигации

Geophysical Journal InternationalЭтот выпускЖурналы РАНГеофизикаКнигиЖурналыOxford Academic
Термин поиска мобильного микросайта

Закрыть

Фильтр поиска панели навигации

Geophysical Journal InternationalЭтот выпускЖурналы РАНГеофизикаКнигиЖурналыOxford Academic
Термин поиска на микросайте

Расширенный поиск

Резюме

Представлен метод расчета поля статического смещения после землетрясения в слоистой сферической земле. На неглубоких уровнях расслоение Земли характеризуется резкими скачками объемных модулей и модулей сдвига на границе Конрада и Мохо, и поэтому его важно учитывать при оценке деформации земной коры. Решение уравнений статического равновесия представляется в виде суперпозиции сфероидальной и тороидальной составляющих, каждая из которых зависит от степени сферической гармоники и тензора момента. Метод, который недавно применялся к задаче о распространении волн на слоистой сферической земле, применяется здесь к полю статических деформаций. Путем представления точечного источника в терминах разрывов вектора смещения-напряжения функция Грина для конкретной геометрии источника выводится напрямую. Представлены численные тесты для проверки точности метода и иллюстрации влияния сферичности и слоистости на рассчитанные поля деформации. Влияние сферичности обычно составляет менее примерно 2% (от максимальной деформации) в пределах 100 км от очага землетрясения на глубине земной коры. Сопоставление между деформацией, рассчитанной для сферической однородной земли и сферической слоистой земли, показывает, что до 20 процентов ошибок были бы внесены, если бы не учитывалось слоистое строение Земли.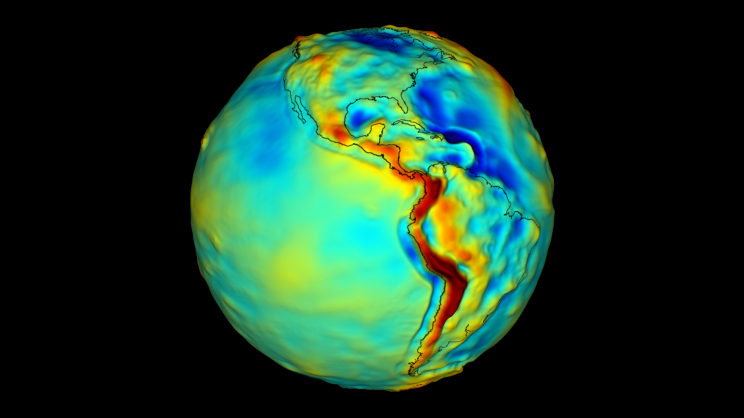 Эффект расслоения наиболее силен для источников с сильной компонентой горизонтального скольжения.

деформация, функции Грина, слоистые среды

Литература

Ричардс

P.G.

1980

Количественная сейсмология

, Vol.

Б.Х. Freeman & Co.

, Сан-Франциско, Луизиана.

Бен-Менахем

А.

Сингх

С.Дж.

1981

Сейсмические волны и источники

Springer-Verlag

, Нью-Йорк, штат Нью-Йорк.

Коэн

ЮК

1984

Постсейсмическая деформация вследствие подкоровой вязкоупругой релаксации после сдвиговых землетрясений

J. geophys. Рез.

4538

–

4544

Далькольмо

Дж.

1993

Synthetische Seismogramme fuer eine sphaerisch symmetrische, nichtrotierende Erde durch direkte Berechnung der Greenschen Funktion

, Diplomarbeit , Institut für Geophysik, Universität Stuttgart.

Эдмондс

А.Р.

1960

Угловой момент в квантовой механике

Princeton University Press

, Принстон, Нью-Джерси.

Фридрих

В.

Далькольмо

Дж.

1995

Полные синтетические сейсмограммы для сферически симметричной земли путем численного расчета функции Грина в частотной области

Geophys, J. Int.

122

537

–

550

Гилберт

Ф.

Дзевонски

А.М.

1975

Применение теории нормального режима к извлечению структурных параметров и механизмов источника из сейсмических спектров

Phil. Транс. Р. Соц. Лонд., А.

278

187

–

269

Йованович

Д.

Хуссейни

М.И.

Чиннери

Массачусетс

1974

Упругие дислокации в слоистом полупространстве — I. Базовая теория и численные методы

Геофиз. Дж. Р. астр. соц.

205

–

217

Йованович

Д.

Хуссейни

М.И.

Чиннери

Массачусетс

1974

Упругие дислокации в слоистом полупространстве — II. Точечный источник

Геофиз. Дж. Р. астр. соц.

219

–

239

Кинг

G.C.P.

Штейн

Р.С.

Рандл

1988

Рост геологических структур при повторных землетрясениях 1. Концептуальные основы

Ж. геофиз. Рез.

, 13

307

—

318.

LAPWOOD

E.R.

USAMI

1981

Свободные колебания Земли

Издательство Кембриджского университета

, Кембридж.

Мацу’ура

М.

Танимото

Т.

Ивасаки

Т.

1981

7 .

Квазистатические смещения вследствие разломов в слоистом полупространстве с промежуточным вязкоупругим слоем

J. Phys. Земля

–

Окада

Ю.

1985

Поверхностная деформация вследствие сдвиговых и растягивающих дефектов в полупространстве

Бюлл. сейсм. соц. Являюсь.

1135

–

1154

Окада

Ю.

1992

Внутренние деформации вследствие сдвиговых и растягивающих дефектов в полупространстве

Бюлл. сейсм. соц. Являюсь.

1018

–

1040

1989

Статическая реакция трансверсально-изотропного и слоистого полупространства на общие источники дислокаций

Физ. Планета Земля. Интер.

103

–

117

Поллитц

Ф.Ф.

1992

Теория постсейсмической релаксации на сферической Земле

Бюлл. сейсм. соц. Являюсь.

422

–

453

Рандл

1980

Статическая упруго-гравитационная деформация слоистого полупространства точечными парными источниками

Ж. геофиз. Рез.

5354

–

5363

Рандл

1982

Вязкоупруго-гравитационная деформация прямоугольным надвигом в слоистой Земле

Ж. геофиз. Рез.

7787

–

7796

Сингх

С. Дж.

1970

Статическая деформация многослойного полупространства внутренними источниками

J. geophys. Рез.

3257

–

3263

Сингх

С.Дж.

Гарг

Н.Р.

1985

О двумерных дислокациях в многослойном полупространстве

Физ. Планета Земля. Интер.

135

–

145

Такеучи

Х.

Сайто

М.

1972

Сейсмические поверхностные волны

, в

Методы вычислительной физики: сейсмология

, стр.

217

–

294

, изд.

Fernbach

Rotenberg

Academic Press

, New York, NY.

Тэтчер

В.

Рандл

Дж. Б.

1979

Модель цикла землетрясений в поднадвиговых зонах

Ж. геофиз. Рез.

5540

–

5556

Васон

Х.Р.

Сингх

С.Дж.

1972

Статическая деформация многослойной сферы внутренними источниками

Геофиз. Дж. Р. астр. соц.

–

Йошиока

С.

Хашимото

М.

Хирахара

К.

1989

7 .

Displacement fields due to the 1946 Nankaido earthquake in a laterally inhomogeneous structure with the subducting Philippine Sea plate—a three-dimensional finite element approach

Tectonophysics

159

121

–

136