Содержание
Пуск ракеты на Восточном увидят дети с онкозаболеваниями, чьи рисунки нанесены на спутник
22 октября, 13:19
КОСМОДРОМ ВОСТОЧНЫЙ /Амурская область/, 22 октября. / ТАСС/. Дети с онкозаболеваниями, рисунки которых нанесены на спутник «Скиф-Д», посмотрят пуск ракеты-носителя «Союз-2.1б» с космодрома Восточный. Об этом сообщила в субботу ТАСС руководитель благотворительного фонда Unity Алена Кузьменко.
В течение года команда фонда вместе с космонавтом Роскосмоса Сергеем Кудь-Сверчковым проводила мастер-классы по арт-терапии для детей с онкологическими заболеваниями в 13 городах России, Замбии и Сербии по программе «Спутник мечты». Среди них — Иркутск, Тулун, Екатеринбург, Ейск, Тамбов, Волгоград, Белград (Сербия), Лусака (Замбия) и другие. Участникам рассказали о космосе и предложили нарисовать мечту.
«Сейчас [на Восточный] прилетели детки из 10 городов, по понятным причинам из Замбии и Сербии не смогли прилететь», — сказала Кузьменко.
Рисунки участников проекта нанесены на таблички и размещены внутри и снаружи спутника «Скиф-Д», запуск которого запланирован на субботу. «Идея состояла в том, чтобы это была не просто сказка, что кто-то когда-то в космос что-то запустит, чтобы они реально своими глазами увидели, что их рисунок, их мечта улетает в космос, для усиления терапевтического эффекта», — отметила руководитель фонда.
«Идея состояла в том, чтобы это была не просто сказка, что кто-то когда-то в космос что-то запустит, чтобы они реально своими глазами увидели, что их рисунок, их мечта улетает в космос, для усиления терапевтического эффекта», — отметила руководитель фонда.
Дети уже посмотрели инфраструктуру и музей космодрома, на интересующие их вопросы отвечал космонавт Сергей Кудь-Сверчков. Позже они смогли познакомиться со специалистами АО «Информационные спутниковые системы им. академика М. Ф. Решетнева», которые наносили рисунки на спутник в течение нескольких месяцев.
«Среди участников проекта есть дети, которые уже в ремиссии, есть детки, которые еще болеют, даже здесь делали укол по химиотерапии — у нас с собой есть врачи, команда медиков, — и, к сожалению, есть детки, которые ушли из жизни за время проекта, не дожили. Для поездки на космодром мы по рекомендации врачей самых крепеньких выбрали», — пояснила Кузьменко.
Пуск ракеты-носителя «Союз-2.1б» с тремя спутниками «Гонец-М» и аппаратом «Скиф-Д» с космодрома Восточный запланирован на 22:57 мск. Примерно через девять минут от третьей ступени отделится головная часть в составе разгонного блока «Фрегат» и четырех космических аппаратов. Выведение разгонным блоком займет чуть более четырех часов.
Примерно через девять минут от третьей ступени отделится головная часть в составе разгонного блока «Фрегат» и четырех космических аппаратов. Выведение разгонным блоком займет чуть более четырех часов.
Это будет первый старт ракеты в этом году с Восточного. Спутники «Гонец-М» впервые отправятся на орбиту с этого космодрома, а «Скиф-Д» станет первым аппаратом, запущенным по программе «Сфера».
О программе «Сфера» президент России Владимир Путин рассказал на прямой линии 7 июня 2018 года. Она подразумевает запуск спутников связи и дистанционного зондирования Земли. По словам бывшего гендиректора Роскосмоса Дмитрия Рогозина, программа будет включать в себя пять спутниковых группировок, предоставляющих услуги телекома, еще пять — наблюдения.
Теги:
ЗамбияРоссияСербия
Детское радио в космосе!
Детское радио в космосе!
На главную
Правила участия
Жюри
Участники конкурса
Поиск по участникам
Имя и фамилия участника
Михаил Майоров, 6 лет
Тольятти
Рисунок «Салют Земле!»
(гуашь)
На благо человечества,
просторы покоряя космоса,
не забываем про отечество
и про родную сторону.
Из путешествий дальних,
с загадочных планет
любимой мамочке Земле
мы шлём большой привет!
Василина Власова, 10 лет
Поселок Мелиоративный
На этой планете дети собираются и обсуждают мультфильмы.И конечно слушают детское радио
Бахолдин Кирилл, 5 лет
Санкт-Петербург
Встреча инопланетян на планете «КАТОК»
Забродина Муза, 8 лет
Сосновоборск , Красноярский край
На картине Муза прилетела в гости на планету к Маленькому Принцу ?
Ермаков Женя, 7 лет
Санкт-Петербург
Жизнь в космосе.МКС,спутники Земли. Летающая тарелка как средство передвижения в будущем.
Софья Ефрем, 8 лет
Чебоксары
Это рисунок о том как космонавты прилетели на Юпитер, но за ними погнались пришельцы с Юпитера.
Победители
919
Николай Рудевич, 6 лет
Москва
Мой стих о Космосе:
Мы летим с тобой в небе синем, голубом.
И в тот час, в тот миг
Наша ракета облетит весь свет.
765
Анастасия Макарова, 12 лет
Санкт-Петербург
Я открываю глаза. Вокруг тишина. Умиротворяющий свет звезд и далеких галактик пробивается сквозь густое, темное покрывало вселенной. Но в этот раз мое внимание поглотила одна маленькая точка, находящаяся совсем рядом от моей родной Земли. Эта маленькая точка — Луна. Когда-то,давно я мечтал, что будущие поколения моих соотечественников покорят её, построят на ней высокотехнологичную базу и смогут свободно передвигаться и изучать её, словно она — вторая Земля. И вот моя мечта сбылась. Я с гордостью наблюдаю за тем, как мои «дети» в скафандрах и на луноходах покоряют этот спутник Земли. Над их головами бисером рассыпаются звезды, и они в восхищении смотрят на нашу Землю, самую красивую планету нашей галактики. И вот я вновь мечтаю. Мечтаю, что, когда я в следующий раз открою глаза, я увижу новые невероятные достижения нашей космонавтики.![]() Я верю, что возможности человека безграничны и он способен на все.
Я верю, что возможности человека безграничны и он способен на все.
772
Соловьева Александра Геннадьевна, 4 лет
Подольск
Я нарисовала как мой папа помогает космонавтам общаться с Землей. Антенна посылает сигнал на Марс. Ангелочек охраняет космонавтов.
147
Голованова Валерия, 8 лет
Санкт-Петербург
На моем рисунке изображена космическая станция МКС. Но от нее открутился винтик, на починку бросились космонавты и космический робот Федор. Он взял новый винтик и прикрутил его. А космонавты чинят датчики кислорода и дырку в корпусе станции.
3
Богословская Кристина, 12 лет
Москва
Меня зовут Кристина, мне 12 лет, я живу в городе Москва. Всю свою жизнь я слушаю Детское радио вместе со своей семьей и не представляю жизни без него, его ведущих и суперинтересных программ. Мне кажется вся Вселенная должна его слушать, тогда всем будет радостно и интересно жить. Надеюсь мой рисунок порадует весь космос!
Мне кажется вся Вселенная должна его слушать, тогда всем будет радостно и интересно жить. Надеюсь мой рисунок порадует весь космос!
2
Варвара Соколова, 12 лет
Санкт-Петербург
Название моего рисунка — «Веснушка и Кипятоша в космосе»
Я изобразила на моем рисунке как мои любимые ведущие детского радио ведут утреннюю программу из космоса. Миллионы детей слушают их на земле!
706
Арина Сердюк, 6 лет
Ульяновск
Моя мечта- побывать в космосе!Увидеть нашу землю!А ещё хочу подарить нашему солнышку цветочек.
4
Торунова Виктория, 10 лет
Богородск, Нижегородская область
На рисунке изображён прекрасный и удивительный мир космоса, который пленяет и завораживает своей красотой космонавтов летящих в ракете. Создать переливы разных оттенков помогли в работе маркеры.
Создать переливы разных оттенков помогли в работе маркеры.
699
Москвина Анна, 9 лет
Москва
Космонавты летят в космос. Один из них покинул космический корабль, тк он идёт на контакт с представителями внеземных цивилизаций.
50
Никитина Мария, 9 лет
Московская область одинцовский район город Кубинка
На рисунке изображён юный астронавт! Он даже игрушку взял с собой в космос. Сидя на лунном камне , смотрит на бесконечную вселенную и мечтает о дальних планетах и о встрече с неземным разумом.
Сказки Детского радио
Тайны старой карты
149 выпусков
Вкусные истории
12 выпусков
Космические приключения
32 выпуска
Книга времен
23 выпуска
Лиза + Папа или Кликни Клаву
6 выпусков
В гостях у дядюшки Филина
34 выпуска
Живой уголок
75 выпусков
Знакомьтесь: Музыка!
25 выпусков
Гонки за лайками.
 Песни
Песни
40 выпусков
Английский для детей
21 выпуск
Новости Детского радио
Спутниковое изображение Земли — Голубой шарик (НАСА)
5 Голубых шариков
Голубой шарик — это термин, используемый для описания изображения нашей планеты, плавающей в бескрайнем космосе .
Именно экипаж миссии «Аполлон-17» впервые сделал культовый спутниковый снимок Земли еще в 1972 году и назвал его «Голубой мрамор».
Но с тех пор НАСА претерпело несколько обновлений этого спутникового снимка Земли , которые доступны в общественное достояние и предназначены для повторного использования.
Вот 5 версий Blue Marble (первым был Apollo 17). Мы также перечислим источники того, как вы можете загрузить изображения Земли НАСА и получить этот полный вид со спутника Земли.
Мы также перечислим источники того, как вы можете загрузить изображения Земли НАСА и получить этот полный вид со спутника Земли.
2002 Blue Marble
Версия Blue Marble 2002 года представляет собой детальное спутниковое изображение Земли с разрешением 1 км на пиксель в естественных цветах.
В течение 4 месяцев он основан на изображениях, полученных с помощью спектрометра визуализации среднего разрешения (MODIS) на борту флагманского спутника Terra.
Безоблачный спутниковый снимок Земли в полном разрешении состоит из 21 600 пикселей в поперечнике и имеет размер более половины гигабайта.
Эти изображения находятся в свободном доступе для общественности на веб-сайте NASA Visible Earth в формате с географической привязкой или в неструктурированном формате.
2005 Blue Marble
Следующий выпуск Blue Marble НАСА был выпущен в 2005 году, что включало значительно улучшенное пространственное разрешение 500 метров на пиксель.
Как и все продукты компании Blue Marble, этот безоблачный глобус можно загрузить с веб-сайта NASA Earth Observatory.
НАСА не только улучшило резкость и качество этой спутниковой карты мира.
Но он также расширил свои возможности по удалению облаков и улучшению визуального представления сезонных изменений.
ПОДРОБНЕЕ: Земная обсерватория НАСА: глобальные данные об окружающей среде и климате .
Этот спутниковый снимок Земли состоит из данных, собранных прибором VIIRS (Visible/Infrared Imager Radiometer Suite) на борту спутника Suomi NPP.
Коллекция Blue Marble 2012 впоследствии побудила к созданию Black Marble (Земля ночью), который представляет собой ночной вид Земли.
В то время как Black Marble 2012 года доступен через веб-сайт EOSDIS Worldview Earthdata, а Blue Marble доступен через Flickr.
Возвращение голубого мрамора (2015)
Версия Blue Marble 2015 года отличается от предыдущих версий. Это связано с тем, что он включает в себя облака и является всего лишь одной фотографией, сделанной 6 июля 2015 года. Северная Америка была относительно безоблачной.
Это связано с тем, что он включает в себя облака и является всего лишь одной фотографией, сделанной 6 июля 2015 года. Северная Америка была относительно безоблачной.
DSCOVR сделал этот спутниковый снимок Земли на расстоянии в миллион миль между Солнцем и нашей планетой (но дальше этой Луны), чтобы получить полное представление о голубом мраморе, который мы называем Землей.
Версия Blue Marble 2015 года доступна на Hyperwall НАСА, а также доступна в видеоформате или в виде текстуры плоской карты.
13.4 Спутниковые орбиты и энергия
Цели обучения
К концу этого раздела вы сможете:
- Описывать механизм круговых орбит
- Найти периоды обращения и скорости спутников
- Определить, связаны ли объекты гравитацией
Луна вращается вокруг Земли. В свою очередь, Земля и другие планеты вращаются вокруг Солнца. Пространство непосредственно над нашей атмосферой заполнено искусственными спутниками на орбите. Мы исследуем простейшую из этих орбит, круговую орбиту, чтобы понять взаимосвязь между скоростью и периодом движения планет и спутников по отношению к их положению и телам, вокруг которых они вращаются.
Мы исследуем простейшую из этих орбит, круговую орбиту, чтобы понять взаимосвязь между скоростью и периодом движения планет и спутников по отношению к их положению и телам, вокруг которых они вращаются.
Круговые орбиты
Как отмечалось в начале этой главы, Николай Коперник впервые предположил, что Земля и все другие планеты вращаются вокруг Солнца по кругу. Он также отметил, что орбитальные периоды увеличиваются с расстоянием от Солнца. Более поздний анализ Кеплера показал, что эти орбиты на самом деле являются эллипсами, но орбиты большинства планет Солнечной системы почти круговые. Орбитальное расстояние Земли от Солнца изменяется всего на 2%. Исключением является эксцентрическая орбита Меркурия, орбитальное расстояние которой варьируется почти на 40%.
Определение орбитальной скорости и орбитального периода спутника намного проще для круговых орбит, поэтому мы делаем это предположение в последующем выводе. Как мы описали в предыдущем разделе, объект с отрицательной полной энергией связан гравитацией и поэтому находится на орбите. Наш расчет для частного случая круговых орбит подтвердит это. Мы ориентируемся на объекты, вращающиеся вокруг Земли, но наши результаты можно обобщить и на другие случаи.
Наш расчет для частного случая круговых орбит подтвердит это. Мы ориентируемся на объекты, вращающиеся вокруг Земли, но наши результаты можно обобщить и на другие случаи.
Рассмотрим спутник массой 9{2}}{р}. [/latex]
Рис. 13.12 Спутник массой m вращается на орбите с радиусом r от центра Земли. Сила гравитации обеспечивает центростремительное ускорение.
Решаем скорость орбиты, учитывая, что м отменяет, чтобы получить орбитальную скорость
[латекс] {v} _ {\ text {орбита}} = \ sqrt {\ frac {G {M} _{\текст{Е}}}{г}}. [/latex]
В соответствии с тем, что мы видели на (Рисунок) и (Рисунок), м не появляется на (Рисунок). Значение g скорость убегания и орбитальная скорость зависят только от расстояния до центра планеты, а , а не от массы объекта, на который воздействуют. Обратите внимание на сходство уравнений для [латекс] {v}_{\text{орбита}} [/латекс] и [латекс] {v}_{\текст{esc}} [/латекс]. Скорость убегания ровно в [латекс] \sqrt{2} [/латекс] раз больше, примерно на 40%, чем орбитальная скорость. Это сравнение отмечено на (Рисунок) и верно для спутника любого радиуса. 9{3}}{G{M}_{\text{E}}}}. [/latex]
Это сравнение отмечено на (Рисунок) и верно для спутника любого радиуса. 9{3}}{G{M}_{\text{E}}}}. [/latex]
В следующем разделе мы увидим, что это представляет третий закон Кеплера для случая круговых орбит. Это также подтверждает наблюдение Коперника о том, что период планеты увеличивается с удалением от Солнца. Нам нужно только заменить [латекс] {M}_{\text{E}} [/латекс] на [латекс] {M}_{\текст{Солнце}} [/латекс] в (Рисунок).
Мы завершаем этот раздел, возвращаясь к нашему более раннему обсуждению астронавтов на орбите, которые кажутся невесомыми, как будто они свободно падают на Землю. По сути, они находятся в свободном падении. Рассмотрим траектории, показанные на (рис.). (Эта цифра основана на рисунке Ньютона в его Principia , а также появлялась ранее в «Движении в двух и трех измерениях».) Все показанные траектории, достигающие поверхности Земли, имеют скорость меньше орбитальной. Астронавты будут ускоряться к Земле по показанным некруговым траекториям и чувствовать себя невесомыми. (На самом деле астронавты готовятся к жизни на орбите, летая на самолетах, которые свободно падают по 30 секунд за раз.) Но при правильной орбитальной скорости поверхность Земли изгибается от них точно с той же скоростью, с какой они падают на Землю. Разумеется, на том же расстоянии от поверхности находится точка круговой орбиты.
(На самом деле астронавты готовятся к жизни на орбите, летая на самолетах, которые свободно падают по 30 секунд за раз.) Но при правильной орбитальной скорости поверхность Земли изгибается от них точно с той же скоростью, с какой они падают на Землю. Разумеется, на том же расстоянии от поверхности находится точка круговой орбиты.
Рис. 13.13 Круговая орбита является результатом выбора тангенциальной скорости таким образом, что поверхность Земли изгибается с той же скоростью, с которой объект падает на Землю.
Мы можем обобщить наше обсуждение орбитальных спутников в следующей стратегии решения проблем.
Стратегия решения задач: орбиты и сохранение энергии
- Определите, применимы ли уравнения для скорости, энергии или периода к рассматриваемой задаче. Если нет, начните с первых принципов, которые мы использовали для вывода этих уравнений.
- Чтобы начать с первых принципов, нарисуйте диаграмму свободного тела и примените закон всемирного тяготения Ньютона и второй закон Ньютона.
 {2}\text{км} [/латекс]. Мы используем (Рисунок) и (Рисунок), чтобы найти орбитальную скорость и период соответственно. 9{3}\,\text{s} [/latex]
{2}\text{км} [/латекс]. Мы используем (Рисунок) и (Рисунок), чтобы найти орбитальную скорость и период соответственно. 9{3}\,\text{s} [/latex], что составляет чуть более 90 минут.
Значение
МКС считается находящейся на низкой околоземной орбите (НОО). Почти все спутники находятся на НОО, включая большинство метеорологических спутников. Спутники GPS на расстоянии около 20 000 км считаются средней околоземной орбитой. Чем выше орбита, тем больше энергии требуется, чтобы вывести его туда, и тем больше энергии нужно, чтобы добраться до него для ремонта. Особый интерес представляют спутники на геостационарной орбите. Все стационарные спутниковые тарелки на земле, направленные в небо, например антенны для приема телевизионных сигналов, направлены на геостационарные спутники. Эти спутники размещены на точном расстоянии и чуть выше экватора, так что их период обращения составляет 1 день. Они остаются в фиксированном положении относительно поверхности Земли.
Проверьте свои знания
Во сколько раз должен измениться радиус, чтобы орбитальная скорость спутника уменьшилась вдвое? Во сколько раз это изменит период?
Показать решение
Пример
Определение массы Земли
Определите массу Земли по орбите Луны.
 {6}\,\текст{с} [/латекс], а 9{24}\,\text{kg} [/latex], которые мы получили на (Рисунок), используя значение g на поверхности Земли. Хотя эти значения очень близки (~ 0,8%), в обоих расчетах используются средние значения. Величина г изменяется от экватора к полюсам примерно на 0,5%. Но Луна имеет эллиптическую орбиту, на которой значение r варьируется чуть более чем на 10%. (Видимый размер полной Луны на самом деле варьируется примерно на эту величину, но это трудно заметить при случайном наблюдении, поскольку время от одной крайности до другой составляет много месяцев.)
{6}\,\текст{с} [/латекс], а 9{24}\,\text{kg} [/latex], которые мы получили на (Рисунок), используя значение g на поверхности Земли. Хотя эти значения очень близки (~ 0,8%), в обоих расчетах используются средние значения. Величина г изменяется от экватора к полюсам примерно на 0,5%. Но Луна имеет эллиптическую орбиту, на которой значение r варьируется чуть более чем на 10%. (Видимый размер полной Луны на самом деле варьируется примерно на эту величину, но это трудно заметить при случайном наблюдении, поскольку время от одной крайности до другой составляет много месяцев.)Проверьте свое понимание
Есть еще одно соображение относительно этого последнего расчета [латекс] {М}_{\текст{Е}} [/латекс]. Мы получили (Рисунок), предполагая, что спутник вращается вокруг центра астрономического тела с тем же радиусом, который используется в выражении для гравитационной силы между ними. Какое предположение делается для обоснования этого? Земля примерно в 81 раз массивнее Луны.
 Луна вращается вокруг точного центра Земли?
Луна вращается вокруг точного центра Земли?Показать решение
Пример
Галактическая скорость и период
Вернемся к (рисунок). Предположим, что галактики Млечный Путь и Андромеда вращаются по круговой орбите друг вокруг друга. Какова будет скорость каждого из них и каков будет их орбитальный период? Предположим, что масса каждого из них составляет 800 миллиардов солнечных масс, а их центры разделены 2,5 миллионами световых лет.
Стратегия
Мы не можем использовать (Рисунок) и (Рисунок) напрямую, потому что они были получены в предположении, что объект массой m вращалась вокруг центра гораздо большей планеты с массой M . Мы определили гравитационную силу на (рис.) с помощью закона всемирного тяготения Ньютона. Мы можем использовать второй закон Ньютона, примененный к центростремительному ускорению любой галактики, чтобы определить их тангенциальную скорость. Из этого результата мы можем определить период орбиты.
 {2}}{{r}_{\text{орбита}}}\hfill \\ \hfill 1.9{18}\,\text{s} [/latex], около 50 миллиардов лет.
{2}}{{r}_{\text{орбита}}}\hfill \\ \hfill 1.9{18}\,\text{s} [/latex], около 50 миллиардов лет.Значение
Орбитальная скорость 47 км/с на первый взгляд может показаться высокой. Но эта скорость сравнима со скоростью убегания от Солнца, которую мы рассчитали в более раннем примере. Чтобы дать еще большую перспективу, этот период почти в четыре раза больше, чем время существования Вселенной.
Фактически, нынешнее относительное движение этих двух галактик таково, что они, как ожидается, столкнутся примерно через 4 миллиарда лет. Хотя плотность звезд в каждой галактике делает маловероятным прямое столкновение любых двух звезд, такое столкновение окажет сильное влияние на форму галактик. Примеры таких столкновений хорошо известны в астрономии.
Проверьте свое понимание
Галактики не являются отдельными объектами. Как гравитационная сила одной галактики, действующая на «ближние» звезды другой галактики, сравнивается с более удаленными? Как это повлияет на форму самих галактик?
Показать решение
См.
 страницу Sloan Digital Sky Survey для получения дополнительной информации о сталкивающихся галактиках.
страницу Sloan Digital Sky Survey для получения дополнительной информации о сталкивающихся галактиках.Энергия на круговых орбитах
В разделе «Потенциальная гравитационная энергия» и «Общая энергия» мы утверждали, что объекты гравитационно связаны, если их полная энергия отрицательна. Аргумент был основан на простом случае, когда скорость была направлена прямо от планеты или к ней. Теперь мы исследуем полную энергию для круговой орбиты и покажем, что полная энергия действительно отрицательна. Как и раньше, мы начнем со второго закона Ньютона, примененного к круговой орбите, 9{}}. [/latex]
Мы видим, что полная энергия отрицательна и имеет ту же величину, что и кинетическая энергия. Для круговых орбит величина кинетической энергии составляет ровно половину величины потенциальной энергии. Примечательно, что этот результат применим к любым двум массам, обращающимся по круговым орбитам вокруг их общего центра масс на расстоянии r друг от друга. Доказательство этого оставлено в качестве упражнения.
 В следующем разделе мы увидим, что очень похожее выражение применимо и к эллиптическим орбитам.
В следующем разделе мы увидим, что очень похожее выражение применимо и к эллиптическим орбитам.Пример
Энергия, необходимая для выхода на орбиту
На (рисунке) мы рассчитали энергию, необходимую для простого подъема 9000-килограммового корабля «Союз » массой 9000 кг с поверхности Земли на высоту МКС, 400 км над поверхностью. Другими словами, мы нашли его изменение потенциальной энергии. Теперь зададимся вопросом, какое полное изменение энергии требуется кораблем «Союз », чтобы поднять его с поверхности Земли и вывести на орбиту с МКС для сближения ((Рисунок))? Сколько из этой полной энергии составляет кинетическая энергия?
Рис. 13.15 Сближение корабля «Союз» с МКС. Обратите внимание, что эта диаграмма не в масштабе; Союз очень мал по сравнению с МКС, и его орбита намного ближе к Земле. (кредит: модификация работ НАСА)
Стратегия
Требуемая энергия — это разница в общей энергии «Союз » на орбите и на поверхности Земли.
 Мы можем использовать (Рисунок), чтобы найти полную энергию Союз на орбите МКС. Но полная энергия на поверхности — это просто потенциальная энергия, поскольку она начинается из состояния покоя. [Обратите внимание, что мы не используйте (рисунок) на поверхности, так как мы не находимся на орбите на поверхности.] Кинетическая энергия может быть найдена из разницы между изменением полной энергии и изменением потенциальной энергии, найденным на (рисунке). В качестве альтернативы мы можем использовать (Рисунок), чтобы найти [латекс] {v}_{\text{орбита}} [/латекс] и вычислить кинетическую энергию непосредственно из этого. Тогда полная требуемая энергия равна кинетической энергии плюс изменение потенциальной энергии, найденное на (рис.).
Мы можем использовать (Рисунок), чтобы найти полную энергию Союз на орбите МКС. Но полная энергия на поверхности — это просто потенциальная энергия, поскольку она начинается из состояния покоя. [Обратите внимание, что мы не используйте (рисунок) на поверхности, так как мы не находимся на орбите на поверхности.] Кинетическая энергия может быть найдена из разницы между изменением полной энергии и изменением потенциальной энергии, найденным на (рисунке). В качестве альтернативы мы можем использовать (Рисунок), чтобы найти [латекс] {v}_{\text{орбита}} [/латекс] и вычислить кинетическую энергию непосредственно из этого. Тогда полная требуемая энергия равна кинетической энергии плюс изменение потенциальной энергии, найденное на (рис.).Раствор
9{11}\,\text{J.} [/latex]
Значение
Кинетическая энергия корабля «Союз » почти в восемь раз превышает изменение его потенциальной энергии, или 90% от общей энергии, необходимой для сближения.
 с МКС. И важно помнить, что эта энергия представляет собой только ту энергию, которую необходимо отдать «Союзу ». С нашей современной ракетной технологией масса двигательной установки (ракетного топлива, его контейнера и системы сгорания) намного превышает массу полезной нагрузки, и этой массе необходимо передать огромное количество кинетической энергии. Таким образом, фактическая стоимость энергии во много раз превышает изменение энергии самой полезной нагрузки.
с МКС. И важно помнить, что эта энергия представляет собой только ту энергию, которую необходимо отдать «Союзу ». С нашей современной ракетной технологией масса двигательной установки (ракетного топлива, его контейнера и системы сгорания) намного превышает массу полезной нагрузки, и этой массе необходимо передать огромное количество кинетической энергии. Таким образом, фактическая стоимость энергии во много раз превышает изменение энергии самой полезной нагрузки.Резюме
- Орбитальные скорости определяются массой тела, находящегося на орбите, и расстоянием от центра этого тела, а не массой гораздо меньшего объекта на орбите.
- Период обращения также не зависит от массы объекта на орбите.
- Тела с сопоставимыми массами вращаются вокруг своего общего центра масс, а их скорости и периоды должны определяться из второго закона Ньютона и закона всемирного тяготения.
9{2} [/латекс]. С кем вы согласны и почему?
Многие спутники размещены на геостационарных орбитах.
 Что особенного в этих орбитах? Сколько таких спутников потребуется для глобальной сети связи?
Что особенного в этих орбитах? Сколько таких спутников потребуется для глобальной сети связи?Показать решение
Задачи
Если бы по орбите Земли двигалась планета, масса которой в 1,5 раза больше массы Земли, каков был бы ее период?
Две планеты на круговых орбитах вокруг звезды имеют скорости v и 2 в . а) Каково отношение радиусов орбит планет? б) Каково соотношение их периодов?
Показать решение
Используя среднее расстояние Земли от Солнца и период обращения Земли, (а) найдите центростремительное ускорение Земли при ее движении вокруг Солнца. (b) Сравните это значение с центростремительным ускорением на экваторе из-за вращения Земли.
Каков радиус орбиты спутника Земли с периодом 1 час? б) Что неразумного в этом результате? 9{7} [/latex] лет вместо этого, какова масса галактики? Такие расчеты используются, чтобы предположить существование другой материи, такой как очень массивная черная дыра в центре Млечного Пути.

(a) Чтобы маленький спутник не дрейфовал на соседний астероид, он выводится на орбиту с периодом 3,02 часа и радиусом 2,0 км. Какова масса астероида? (b) Кажется ли эта масса приемлемой для размера орбиты?
Показать решение
Луна и Земля вращаются вокруг своего общего центра масс, который находится примерно в 4700 км от центра Земли. (это 169{4} [/latex] световых лет. (Световой год — это расстояние, пройденное светом за 1 год.) Вычислите центростремительное ускорение Солнца на его галактической орбите. Подтверждает ли ваш результат утверждение о том, что на Солнце может быть расположена почти инерциальная система отсчета? б) Вычислите среднюю скорость движения Солнца по его галактической орбите. Ответ вас удивляет?
Показать решение
Геосинхронный спутник Земли — это спутник с периодом обращения ровно 1 день. Такие орбиты полезны для связи и наблюдения за погодой, потому что спутник остается над одной и той же точкой на Земле (при условии, что он вращается в экваториальной плоскости в том же направлении, что и вращение Земли).


 {2}\text{км} [/латекс]. Мы используем (Рисунок) и (Рисунок), чтобы найти орбитальную скорость и период соответственно. 9{3}\,\text{s} [/latex]
{2}\text{км} [/латекс]. Мы используем (Рисунок) и (Рисунок), чтобы найти орбитальную скорость и период соответственно. 9{3}\,\text{s} [/latex] {6}\,\текст{с} [/латекс], а 9{24}\,\text{kg} [/latex], которые мы получили на (Рисунок), используя значение g на поверхности Земли. Хотя эти значения очень близки (~ 0,8%), в обоих расчетах используются средние значения. Величина г изменяется от экватора к полюсам примерно на 0,5%. Но Луна имеет эллиптическую орбиту, на которой значение r варьируется чуть более чем на 10%. (Видимый размер полной Луны на самом деле варьируется примерно на эту величину, но это трудно заметить при случайном наблюдении, поскольку время от одной крайности до другой составляет много месяцев.)
{6}\,\текст{с} [/латекс], а 9{24}\,\text{kg} [/latex], которые мы получили на (Рисунок), используя значение g на поверхности Земли. Хотя эти значения очень близки (~ 0,8%), в обоих расчетах используются средние значения. Величина г изменяется от экватора к полюсам примерно на 0,5%. Но Луна имеет эллиптическую орбиту, на которой значение r варьируется чуть более чем на 10%. (Видимый размер полной Луны на самом деле варьируется примерно на эту величину, но это трудно заметить при случайном наблюдении, поскольку время от одной крайности до другой составляет много месяцев.) Луна вращается вокруг точного центра Земли?
Луна вращается вокруг точного центра Земли? {2}}{{r}_{\text{орбита}}}\hfill \\ \hfill 1.9{18}\,\text{s} [/latex], около 50 миллиардов лет.
{2}}{{r}_{\text{орбита}}}\hfill \\ \hfill 1.9{18}\,\text{s} [/latex], около 50 миллиардов лет. страницу Sloan Digital Sky Survey для получения дополнительной информации о сталкивающихся галактиках.
страницу Sloan Digital Sky Survey для получения дополнительной информации о сталкивающихся галактиках. В следующем разделе мы увидим, что очень похожее выражение применимо и к эллиптическим орбитам.
В следующем разделе мы увидим, что очень похожее выражение применимо и к эллиптическим орбитам.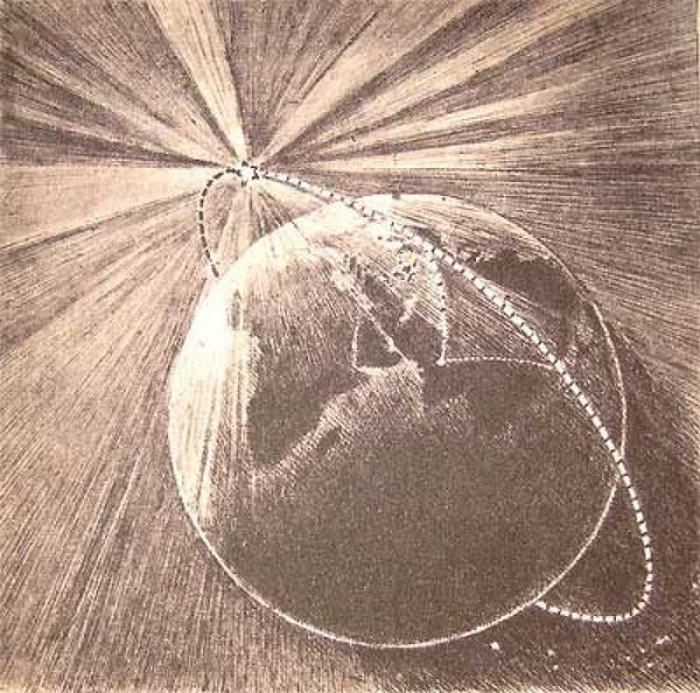 Мы можем использовать (Рисунок), чтобы найти полную энергию Союз на орбите МКС. Но полная энергия на поверхности — это просто потенциальная энергия, поскольку она начинается из состояния покоя. [Обратите внимание, что мы не используйте (рисунок) на поверхности, так как мы не находимся на орбите на поверхности.] Кинетическая энергия может быть найдена из разницы между изменением полной энергии и изменением потенциальной энергии, найденным на (рисунке). В качестве альтернативы мы можем использовать (Рисунок), чтобы найти [латекс] {v}_{\text{орбита}} [/латекс] и вычислить кинетическую энергию непосредственно из этого. Тогда полная требуемая энергия равна кинетической энергии плюс изменение потенциальной энергии, найденное на (рис.).
Мы можем использовать (Рисунок), чтобы найти полную энергию Союз на орбите МКС. Но полная энергия на поверхности — это просто потенциальная энергия, поскольку она начинается из состояния покоя. [Обратите внимание, что мы не используйте (рисунок) на поверхности, так как мы не находимся на орбите на поверхности.] Кинетическая энергия может быть найдена из разницы между изменением полной энергии и изменением потенциальной энергии, найденным на (рисунке). В качестве альтернативы мы можем использовать (Рисунок), чтобы найти [латекс] {v}_{\text{орбита}} [/латекс] и вычислить кинетическую энергию непосредственно из этого. Тогда полная требуемая энергия равна кинетической энергии плюс изменение потенциальной энергии, найденное на (рис.). Что особенного в этих орбитах? Сколько таких спутников потребуется для глобальной сети связи?
Что особенного в этих орбитах? Сколько таких спутников потребуется для глобальной сети связи?
