Содержание
The Noobs` Science: Теория относительности простым языком
Договоримся обозначать теорию относительности ТО, специальную — СТО, общую — ОТО.
Если мы начнём сравнивать теорию относительности с квантовой механикой, то заметим, что создатели квантовой механики — десятки учёных, в то время как единственной центральной фигурой всей теории относительности является Альберт Эйнштейн.
Понимание этой теории поможет в восприятии многих физических явлений. Она способна объяснить, почему траектория света может искривляться, вопреки принципу Ферма о прямолинейном распространении света, или же почему не стоит опасаться чёрных дыр.
В то же время теория относительности учит критическому мышлению. Допустим, если появится новость о создании космического корабля со сверхсветовой скоростью, то распознать в ней фейк не составит труда, ведь никакая скорость не может быть больше скорости света.
В конце концов, теория относительности объяснила множество парадоксальных явлений, которые раньше не подлежали никакому объяснению со стороны учёных.
Любая физика начинается с классической механики, то есть описания макроскопического мира, его объектов и движения этих объектов. Когда объект достигает очень больших скоростей, он перестаёт подчиняться классической механике и начинает подчиняться релятивистской.
Что такое «большие скорости»? Всё сравнивается со скоростью света: если объект движется со скоростью ненамного меньшей скорости света, то он перестаёт подчиняться законам классической механики.
Общая и специальная теория относительности
Существуют общая и специальная теории относительности. Первой появилась специальная — она не учитывает гравитацию, которую, к сожалению, невозможно игнорировать. Общая теория относительности учитывает гравитацию и из неё вытекают интересные следствия, такие как красные гравитационные смещения, гравитационные волны или чёрные дыры.
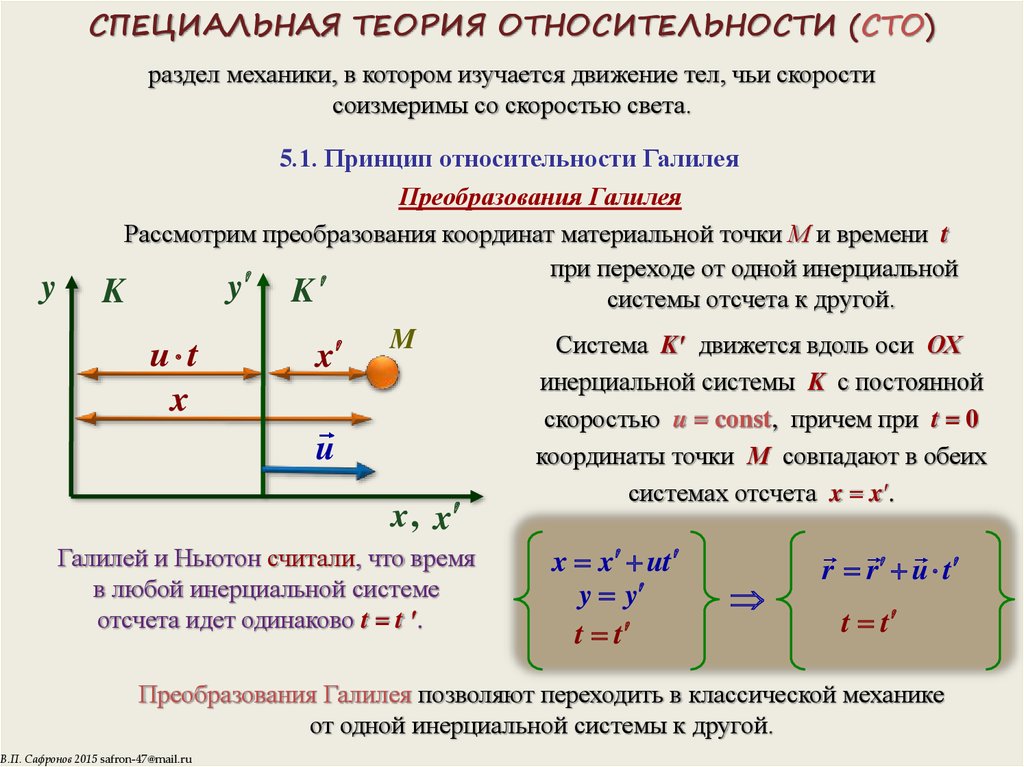
Есть одна принципиально важная тема для понимания ТО — принцип относительности Галилея:
Физические процессы в инерциальных системах отсчёта (договоримся обозначать их ИСО, системы отсчёта — СО) протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения.
Если бросить камень и перо вниз в Алматы и в Чикаго одновременно, из одной и той же высоты, пренебрегая сопротивлением воздуха (провести эксперимент в вакууме), то и перо, и камень приземлятся одновременно, из чего вытекает вывод — все покоящиеся системы отсчёта эквивалентны друг другу.
Следующий мысленный эксперимент — вы находитесь в вагоне поезда, который двигается с постоянной скоростью, вагон звукоизолированный, герметичный, в нем нет окон, поезд не трясётся по рельсам, а внутри нет часов. Вы решили заснуть.
Вопрос: как после пробуждения определить, прибыли ли вы или нет?
Ответ: никак. Вывод — система, двигающаяся с постоянной скоростью, эквивалентна покоящейся системе, и можно спокойно переходить из одной в другую, законы физики при этом не изменятся.
Нет смысла утверждать, покоится ли объект, либо двигается, если не уточнить относительно чего он покоится или двигается. Например, лежа на диване, мы покоимся относительно земли, но двигаемся относительно Солнца, так как сама Земля постоянно вращается вокруг Солнца.
Также стоит отметить, что из одной ИСО можно перейти в другую банальным использованием простейших формул. Например, если человек в поезде, движущимся со скоростью 60 км/ч, перемещается со скоростью 5 км/ч в направлении движения поезда, то относительно неподвижного наблюдателя у вокзала, человек в поезде перемещается со скоростью 65 км/ч. Очень просто.
Однако, существовало одно значительное противоречие — свет. Он не подчиняется этим правилам и в любой ИСО двигается с одинаковой скоростью (примерно 300 000 км/сек). То есть, что для наблюдателя у вокзала, что для пассажира поезда, теперь уже с фонарём в руке, свет бы удалялся с одинаковой скоростью, несмотря на то что может казаться, что относительно неподвижного наблюдателя у вокзала, свет бы удалялся с большей скоростью — не 300 000 км/c, а 300 000 + скорость поезда в секунду.
Эйнштейн решает эту проблему в 1905 году и корректирует классические постулаты Галилея:
- Все физические явления — не только механические (только о механических говорилось у Галилея), — протекают одинаково во всех ИСО, то есть добавляются слабое, сильное и электромагнитное взаимодействия.
- Существование предельной скорости распространения взаимодействия: любые взаимодействия между телами распространяются в пустоте с универсальной конечной скоростью, не зависящей от движения тел и равной скорости света в вакууме. Иными словами, существует самая большая возможная скорость — скорость света, выше которой не может быть ни одна скорость.
Какие явления описывает специальная теория относительности?
Релятивистский эффект замедления времени
Представьте, две одинаковые ракеты летят с одинаковой скоростью, одна находится над второй. В какой-то момент времени одна ракета посылает световой сигнал второй. Если вы переместитесь во вторую ракету, относительно вас световой сигнал идёт перпендикулярно, однако относительно неподвижного свидетеля, который наблюдает за ситуацией «в целом», свет пройдёт более длинный путь, как бы по диагонали.
Почему длиннее? Вспоминаем геометрию — гипотенуза всегда длиннее катета.
Однако, скорость света одинакова в обоих СО, время вроде бы тоже должно быть одинаково, но S2>S1. Противоречие (на рисунке с — скорость света).
Значит, в СО движущейся ракеты время замедлилось, потому что в этой СО свет прошёл меньшее расстояние. И это действительно так. При скоростях, близких к скоростям света, время замедляется.
Релятивистский эффект сокращения длины
Допустим, ракета двигается со скоростью, составляющей 83 процента от скорости света (примерно 243 000 км/сек), тогда относительно неподвижного наблюдателя, её длина уменьшится в два раза в направлении движения.
То есть если её скорость направлена вдоль оси Х, то длина также сократится вдоль оси Х, оставаясь неизменной вдоль осей Y и Z (другими словами, сократится только длина, или ширина, или высота, в зависимости от ориентации ракеты, но не все параметры сразу).
Кстати, время для этой ракеты замедлится в два раза. Если же мы перейдём в СО ракеты, то длина останется прежней, однако все окружающие её объекты сократятся в два раза.
Звучит всё невероятно. Теория подтвердилась экспериментом только в 1952 году. Есть такие частицы — пионы, время жизни которых составляет 2,6 *10−8 сек, и они двигаются со скоростью света. Если посчитать, какое расстояние пройдёт пион за всю жизнь, двигаясь со скоростью света, то получится, что он пройдёт только 7,5 м.
Однако, установка, которая «плевала» этими пионами, и приёмник находились в 100 метрах друг от друга. То есть, пионы бы не долетели до приёмника без законов СТО. Но если мы подключаем ТО, то время жизни частицы становится в 100 раз больше, то есть она способна пролететь не 7,5 м, а 750 м.
Что же происходит в СО частицы? В СО частицы она также пролетает 7,5 м., однако для неё 100 м. между ней и приёмником превращаются в 1м, согласно эффекту сокращения длины.
Когда статья Эйнштейна о специальной ТО была опубликована, особой огласки она не получила. Эйнштейн думал над тем, как включить гравитацию в свою теорию. На тот момент везде царили законы гравитации Ньютона.
Благодаря им открыли Нептун.
Дело в том, что при наблюдении за Ураном выяснили, что при всех силах, которые на него действуют, у Урана должна быть совершенно другая скорость движения. Предположили существование ещё одной планеты за Ураном, которая бы объясняла данное значение скорости. В 1846 году появляется новый телескоп, обнаруживают Нептун, подтверждаются законы Ньютона.
Однако по Ньютону, если мы сдвинем Солнце, произойдёт моментальное изменение силы, с которой Солнце притягивается к другим объектам. Скорость изменения силы бесконечно большая, что противоречит СТО (так как существует максимальное значение скорости, равное скорости света, бесконечной скорости никак не может быть).
Эйнштейн заметил ещё одну вещь: если наблюдатель находится вблизи массивного тела, то чем ближе он к этому телу, тем медленнее течёт его время. Например, в любом доме на Земле время на первом этаже течет медленнее, чем на втором. Правда, разница оказывается очень маленькой:
3*10−16 сек = 0.
0000000000000003 сек
Однозначно со временем что-то не так. Эйнштейн решил, что в этом ключ ко всей его теории. Однако, он оказался неправ.
Преподаватель Эйнштейна по математике Герман Минковский, обнаружив его работу, выдвинул свою точку зрения: нет смысла отдельно рассматривать пространство и время, физику необходимо рассматривать в четырёхмерном пространстве.
Для нас странно, что длина объекта сокращается при больших скоростях, однако Минковский считал, что нет никакого сокращения длины в четырёхмерном пространстве, и что просто проекция четырехмерного объекта в трёхмерный начинает изменяться. Четвёртой осью в четырёхмерном пространстве считается время.
Чтобы понять, что такое проекция, вспомните свою тень. Ваше тело находится в трехмёрном пространстве, однако ваша тень — на плоскости, то есть в двумерном пространстве. Она и есть проекция вашего трёхмерного тела на двумерную плоскость.
Тень редко передаёт точные пропорции и размеры человека, соответственно, если события, которые происходят в четырёхмерном пространстве, проектировать на наш, трёхмерный, то появляются искажение, допустим, в виде сокращения длины при скоростях, близких к скоростям света.
Мы реально живём в четырёхмерном пространстве?
И да, и нет. Пространство-время искривлено находящимися в нём массой и энергией. Другие же объекты чувствуют искривление пространства-времени и следуют так, как им указывает пространство.
С 1908 по 1914 Эйнштейн предпринял ряд безуспешных попыток построить такую модель гравитации, которая согласовалась бы со СТО. Наконец, в 1915 году он опубликовал ОТО.
Эйнштейн высказал предположение революционного характера: гравитация — это не обычная сила, а следствие того, что пространство-время не является плоским, как считалось раньше; оно искривлено распределёнными в нём массой и энергией. Такие тела, как Земля, вовсе не принуждаются двигаться по искривлённым орбитам гравитационной силой; они движутся по линиям, которые в искривлённом пространстве более всего соответствуют прямым в обычном пространстве и называются геодезическими.
Что такое геодезическая линия?
Геодезическая линия — это линия, соответствующая самому короткому пути между двумя точками.
Очевидно, что в идеальном двумерном пространстве это просто прямой отрезок, соединяющий две точки. Однако, что будет, если мы начнём поверхность искривлять, добавляя массу, а вместе с ней и энергию? Прямые будут также прогибаться.
В пределах полученной искривлённой плоскости, искривлённая прямая будет уже называться геодезической, и, тем не менее на искривлённой плоскости она будет продолжать соответствовать самому короткому пути.
Допустим, вы совершаете трип по холмистой местности и хотите пройти как можно более короткий путь. У вас есть макет рельефа этой местности. Очень сложно прочертить самый короткий маршрут в этом случае. Но если «сплюснуть» данный рельеф в идеальную плоскость, предварительно отметив начальную и конечную точку, то можно потом просто соединить эти две точки уже в двумерной плоскости — получится прямая; опять искривить плоскость до «холмистой», и вот, пожалуйста — у вас начертанный самый короткий путь.
Например, поверхность Земли — искривлённое двумерное пространство, так как любую координату можно задать долготой и широтой.
Поскольку самый короткий путь между двумя аэропортами — по геодезической, диспетчеры всегда задают пилотам именно такой маршрут.
Согласно ОТО, тела всегда перемещаются по прямым в четырёхмерном пространстве-времени, но мы видим, что в нашем трёхмерном пространстве они движутся по искривлённым траекториям. Понаблюдайте за самолётом над холмистой местностью. Сам он летит по прямой в трёхмерном пространстве, а его тень перемещается по кривой на двумерной поверхности Земли.
Как это может выглядеть?
На гифке мы видим синее полотно, олицетворяющее плоскость пространства-времени. Когда мы добавляем груз, ткань искривляется: чем массивнее груз, тем больше искривляется ткань.
А запущенные шарики двигаются по эллиптическим орбитам до тех пор, пока по спирали не провалятся. Они олицетворяют планеты Солнечной системы, но планеты не проваливаются, потому что в космосе нет трения, на которое тратится кинетическая энергия шариков при соприкосновении с полотном.
Эйнштейн также «схватился» за нерешённую на тот момент задачу — задачу о смещении перигелия Меркурия.
Перигелий — ближайшая к Солнцу точка. Солнце находится в одном из фокусов эллиптической орбиты Меркурия.
Эллиптическая орбита Меркурия поворачивается со временем. По предсказаниям законов гравитации Ньютона, смещение Перигелия должно было составлять 1,28 угловой секунды, но по факту оно составляло 1,38 угловой секунды. (1 угловая секунда = 1/3600 от одного градуса).
Можно было бы списать на погрешность измерений, но погрешность составляла только 0,01 угловой секунды — ошибиться на 0,1 угловой секунды было невозможно. В конце концов, после открытия ОТО из уравнений теории вытекало именно такое значение смещения, которое фактически наблюдалось.
Таким образом, теория подтвердилась экспериментально и это был далеко не первый раз. Теория внесла колоссальный вклад в науку того времени, будучи проигнорированной научным сообществом на своём зародыше, она окончательно сместила Ньютоновскую средневековую физику, на которую уповали все учёные.
Подробнее о следствиях ОТО мы расскажем в следующей статье.
Читай нас в
Инстаграм
и
Телеграм
Теория относительности и зачем она нужна: часть 1, СТО: yuritkachev — LiveJournal
Словосочетание «теория относительности», как и имя её автора Альберта Эйнштейна, слышал, наверное, каждый. Увы (хотя основы теории относительности и приходят в школе) многие слабо или не до конца понимают, о чём идёт речь. Попытаемся это дело исправить.
Итак, теория относительности, а точнее, специальная теория относительности, СТО (есть ещё общая теория относительности, ОТО, но о ней в следующий раз) описывает движение тел со скоростями, сравнимыми со скоростью света – в отличие от классической механики, которая «работает» с привычными нам скоростями.
Точнее, даже не так. СТО описывает процессы, происходящие при любых скоростях. Но просто при малых скоростях некоторые эффекты, становящиеся значимыми при скоростях больших, себя практически не проявляют, и можно довольствоваться сравнительно более простыми формулами классической механики.
А если мы рассматриваем условия, в которых эти эффекты уже отбросить нельзя, то тут-то нам на помощь и приходит СТО. Если же в формулах СТО считать скорости пренебрежимо малыми по сравнению со скоростями света, то мы получим всё те же уравнения классической механики.
Иными словами, классическая механика является составной частью СТО, её упрощением для частного случая малых скоростей.
Интересно, что большинство эффектов теории относительности были открыты, что называется, на кончике пера, и лишь потом подтверждены экспериментально.
СТО стала результатом многолетних попыток состыковать два хороших, годных раздела физики, категорически не желавших «работать» вместе: классическую механику и электродинамику.
Одним из краеугольных камней классической механики является так называемый принцип относительности, который гласит: в двух системах отсчёта, покоящихся друг относительно друга или движущихся относительно друг друга равномерно или прямолинейно, все законы физики работают одинаково.
Если быть уж до конца точным, в классической механике этот принцип, ещё называющийся принципом Галилея, распространяется лишь на законы этой самой механики.
Тот самый Галилей
Однако Галилея и его современников можно понять: в их времена-то других отраслей физики, кроме механики, толком и не было. Откуда вопрос: а распространяется ли принцип относительности, к примеру, и на электродинамику? С одной стороны, было логично предположить, что да. С другой – такое предположение порождало ряд неприятных проблем.
В электродинамике ту же фундаментальную роль, которую в механике играют три закона Ньютона, играют четыре уравнения Максвелла. И в некоторые из них в качестве параметра входит скорость света. С точки зрения электродинамики Максвелла, скорость света – универсальная мировая константа, вроде заряда электрона или гравитационной постоянной.
Но это плохо согласуется с классической механикой, в которой скорость – понятие относительное, зависящее от системы отсчёта.
Если мы будем измерять скорость автомобиля, неподвижно стоя на земле, то мы получим одно значение. Если же проделаем все те же процедуры, находясь в другом движущемся авто, то получим и другое значение скорости. Пассажир, идущий по проходу в салоне авиалайнера, движется с одной скоростью относительно других пассажиров и совсем с другой – относительно людей в аэропорту, откуда этот лайнер вылетел. То есть, скорость в классической механике зависит от точки зрения – а точнее, от системы отсчёта.
Но с точки зрения электродинамики для скорости света это не работает. И если наш пассажир самолёта включит фонарик, то испускаемые им фотоны будут лететь с одной и той же скоростью как для самого пассажира, так и для наблюдателей в аэропорту.
Это может показаться парадоксальным, и, чтобы объяснить это, можно привлечь на помощь следующие рассуждения. Дело в том, что универсальной константой, по всей видимости, является не сама по себе скорость света в вакууме, а просто некая предельно достижимая в нашей Вселенной скорость.
И свет движется именно с этой максимальной скоростью ввиду того, что его частицы, фотоны, не имеют массы покоя. Соответственно, ни в одной системе отсчёта свет не может двигаться ни быстрее, ни медленнее – просто потому, что может двигаться только так.
Однако отсюда следует противоречие: в электродинамике скорость света абсолютна, в классической механике, где действует принцип Галилея – относительна. И если мы хотим совместить две теории, то нам надо отказаться либо от принципа Галилея, либо от постулата об абсолютности скорости света. Но оба утверждения казались верными и подтверждались экспериментально. И как быть?
Эйнштейн решил пойти другим путём: он решил признать оба постулата верными и попытаться на этом теоретическом базисе построить непротиворечивую теорию.
Итак, вот два постулата СТО, из которых следует всё остальное:
1. Законы физики и природы вообще одинаковы во всех системах отсчёта, движущихся прямолинейно и равномерно друг относительно друга (классическая механика).
2. Скорость света – универсальная константа, независимая от выбора системы отсчёта (электродинамика).
Теперь дело было за теорией, которая позволяла совместить оба эти постулата без противоречий. Но для этого надо понять, о какого рода противоречиях идёт речь. Рассмотрим одно из них.
Представим себе космический корабль, отправившийся в полёт со скоростью в 0,5 скорости света. Представим себе также, что некий злоумышленник заложил на борт этого взрывного устройства бомбу с часовым механизмом, которая должна сработать через 1,7 года после старта корабля.
Предположим, что через год после старта спецслужбы поймали террориста и узнали о бомбе. Они хотят сообщить о ней экипажу корабля, чтобы взрывное устройство можно было бы найти и обезвредить. Они посылают в космос радиосообщение (которое летит, как понятно, со скоростью света). Вопрос: успеет ли сообщение достичь корабля?
Давайте посмотрим на ситуацию с точки зрения землян. До взрыва остаётся 0,7 года.
За это время корабль, движущийся со скоростью в 0,5 скорости света, пролетит 0,35 световых года и будет находиться на расстоянии в 0,85 световых года от Земли. Очевидно, что радиосигнал, движущийся со скоростью света, за оставшиеся до взрыва 0,7 года не успеет покрыть расстояния в 0,85 световых лет. Проще говоря, предупреждение не успеет. Корабль взорвётся.
Но теперь давайте посмотрим на ситуацию с точки зрения пассажиров корабля. В их системе отсчёта корабль неподвижен: не он удаляется от Земли, а Земля удаляется от него. Но для путешествия сигнала к кораблю факт удаления Земли от корабля уже не важен, ведь сигнал покинул Землю и движется независимо от неё с абсолютной скоростью света. Иными словами, с точки зрения наблюдателя на корабле сигнал дойдёт ровно за полгода. А значит, экипаж получит сообщение за 0,2 года до взрыва и успеет обезвредить бомбу.
А теперь давайте вдумаемся: в двух разных системах отсчёта мы получаем совершенно различный исход событий.
А этого не может быть ни с точки зрения принципа относительности, ни с точки зрения банального здравого смысла.
То есть, второй постулат СТО явно противоречит первому. А точнее, он противоречит ему во всех без исключения случаях, кроме одного: если для пассажиров корабля и наблюдателей на Земле течёт одинаково.
Вот это-то предположение и поставил под сомнение Эйнштейн.
Не знаю, что курил Эйнштейн, но он делал это правильно
Что если, предположил он, в движущейся системе отсчёта время движется медленнее, чем в неподвижной? В этом случае, действительно, парадокс с кораблём, который взрывается в одной системе отсчёта и остаётся целым в другой, можно разрешить.
Проще говоря, с точки зрения земных наблюдателей свет действительно достигнет корабля в тот момент, когда корабля на самом деле не должно уже существовать. Но в «замедленном» времени корабля (в котором, кстати, тикает и таймер бомбы!) на самом деле с момента старта пройдёт куда меньше времени.
И поэтому на самом деле никакого взрыва не произойдёт – бомбу успеют обезвредить.
Гипотеза о том, что время не является чем-то универсальным, а течёт по-разному для разных наблюдателей, является краеугольным камнем теории относительности. Собственно, Специальную теорию относительности в этом смысле можно считать расширением классической механики на ситуации, в которых время перестаёт быть абсолютным.
В своей фундаментальной работе «К электродинамике движущихся тел», с которой и началась Специальная теория относительности, Эйнштейн из достаточно простых по сути соображений вывел формулу для сокращения времени, а точнее, для соотношения временных промежутков, измеренных в движущейся и неподвижной системе координат. И хотя я обещал не «грузить» читателя формулами, это знаменитое соотношение я считаю нужным привести:
Здесь Δt0 – промежуток времени в покоящейся системе отсчёта, Δt – соответствующий промежуток времени в движущейся системе, V – скорость этой системы, а с – скорость света, одинаковая для всех систем.
Хорошо видно, что при скорости V существенно меньшей скорости света (классическая механика) никакого сокращения времени не происходит, но чем больше скорость, тем сильнее сокращается временной промежуток в движущейся системе.
Простая иллюстрация к рассуждениям Эйнштейна, с помощью которых он вывел свою формулу. Нет, правда, это на самом деле достаточно просто
Этот эффект называется релятивистским (от слова relativity — относительность) сокращением времени.
Но как может время, которое кажется нам некоей универсальной величиной, меняться в зависимости от такой малости, как скорость движения часов, это время измеряющих? На самом деле, это вовсе не так необъяснимо, как кажется. Для этого нужно представить себе время не как некий независимый параметр, а как четвёртое измерение нашего пространства, а точнее, пространства-времени. И говорить уже не о «течении времени», а о движении наблюдателя вдоль временной оси – подобно тому, как этот наблюдатель может передвигаться вдоль пространственных осей координат.
В этой аналогии действительно нет ничего странного в «неодинаковости» времени. Нас ведь не смущает, что перемещаться в пространстве можно с разной скоростью? Так почему же должна смущать возможность движения с разной скоростью «по оси» времени?
Собственно, теория относительности и «работает» с четырёхмерным пространством-временем. Фактически, математический аппарат СТО преимущественно состоит в переводе привычных нам трёхмерных процессов в четырёхмерную систему и наоборот. К примеру, вводится понятие расстояния между событиями не только в пространстве, но и во времени – так называемого пространственно-временного интервала, или просто интервала. И если рассмотреть нашу аналогию с ракетой с точки зрения такого подхода, окажется, что никаких противоречий и нет. А видели мы их лишь потому, что привыкли к «трёхмерной» логике – удобной и интуитивно-понятной, но, увы, неполной и не отражающей всех особенностей Вселенной.
Классический пример отличия СТО от привычной реальности – так называемая относительность одновременности.
Мы привыкли, что если два события происходят одновременно, то эта одновременность будет также сохраняться для всех систем отсчёта. Если в самолёте, о котором мы упоминали выше, пассажир уронит яблоко, то оно упадёт на пол одновременно и для пассажира, и для наблюдателя в аэропорту. Однако в СТО так уже не получается.
Действительно, представим себе вагон поезда, с релятивистской скоростью проезжающий мимо некоей платформы. В центре вагона сидит один наблюдатель. Второй стоит на платформе. В тот момент, когда оба наблюдателя находятся друг напротив друга, наблюдать-пассажир зажигает спичку.
С его точки зрения свет этой спички достигнет передней и задней стенки вагона за одно и то же время: в его системе отчёта вагон неподвижен, он находится в его центре.
Но в системе отсчёта наблюдателя на платформе всё произойдёт немного не так: свет от спички (скорость которого, напомним, одинакова и в системе отсчёа пассажира, и системе отсчёта наблюдателя на платформе) будет двигаться к обоим стенкам вагона с одинаковой скоростью, но, пока он это делает, стенки вагона сами будут двигаться: передняя – удаляться от наблюдателя, задняя – приближаться к нему.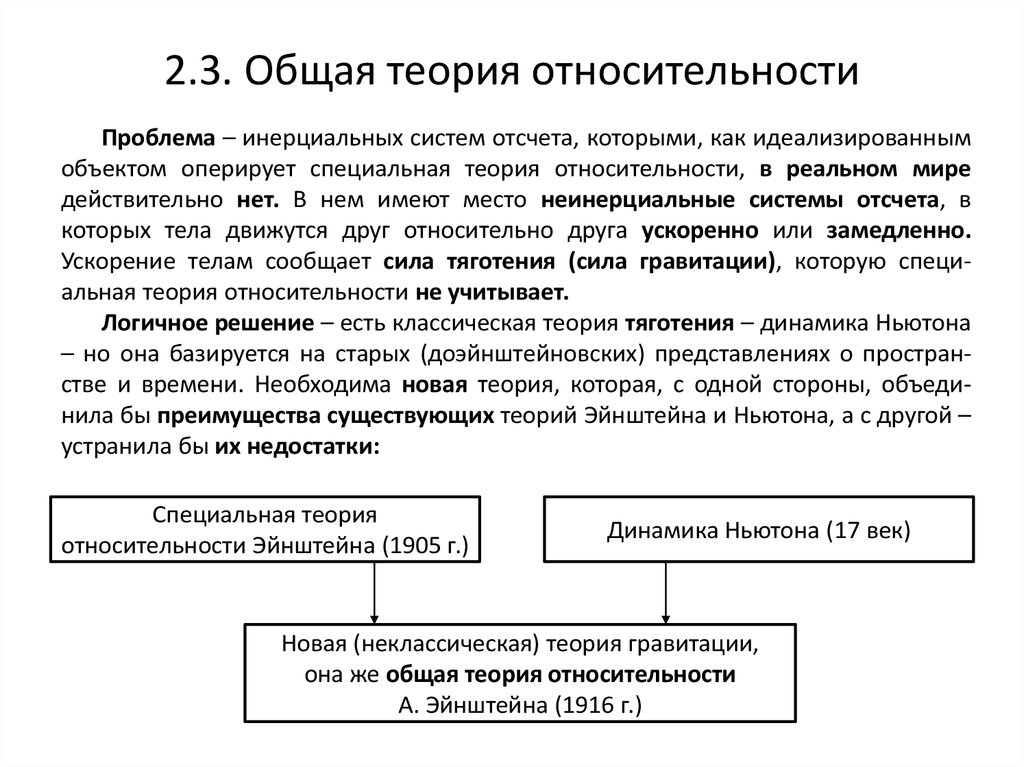
И поэтому свет списки с точки зрения наблюдателя достигнет задней стенки быстрее, чем передней.
Это и есть относительность одновременности: событие (достижение светом стенок вагонов) происходит одновременно для одного наблюдателя и неодновременно – для другого.
На самом деле и при меньших скоростях происходит всё то же самое. Просто из-за малости скоростей релятивистские эффекты незаметны, и события кажутся нам примерно одинаковыми.
Но это ещё не всё. Оказывается, расстояния и размеры предметов в движущихся друг относительно друга системах отсчёта тоже изменяются!
Представим себе, что два человека решили измерить длину некоего протяжённого линейного объекта – скажем, некоей трубы длиной в несколько десятков километров. Для этого один из них отправляется в путь вдоль этой трубы на некоем транспортном средстве, движущимся с известной скоростью. Достаточно замерить время, которое понадобится на то, чтобы добраться с одного конца трубы до другого, умножить на скорость движения – и вот она, длина трубы!
Предположим, что наши наблюдатели для вящей точности решили засечь время независимо друг от друга.
В этом случае к их удивлению выяснится, что длина трубы у них получилась разная! Потому что из-за релятивистского сокращения времени часы у движущегося и неподвижного наблюдателя покажут разное время!
Действительно, пусть неподвижный наблюдатель получил, что путь занял промежуток времени Δt0, и с его точки зрения длина трубы будет равной Vx Δt0. Но для движущегося со скоростью V наблюдателя этот промежуток времени сократится по формуле сокращения времени. Соответственно, длина трубы покажется ему равной:
то есть, окажется меньшей, чем у неподвижного наблюдателя. Если теперь интерпретировать ситуацию в системе отсчёта двигавшегося наблюдателя, где он сам был неподвижен, а труба двигалась относительно него, то получится, что длина движущегося объекта для неподвижного наблюдателя уменьшилась по сравнению с длиной, измеренной в неподвижной системе отсчёта (её ещё называют собственной для этого предмета).
Впоследствии были получены релятивистские формулы для многих других процессов и законов динамики и механики.
Несмотря на всю свою красоту и математическую стройность, теория относительности была слишком революционной, и многими была воспринята в штыки. Сотни теоретиков искали «дыры» в этой теории, и сотни экспериментаторов задавались целью её опровергнуть. Эти усилия пошли на пользу науке: в настоящее время Специальная теория относительности является одной из лучше всего проработанных и экспериментально доказанных теорий современной физики.
К примеру, проведены эксперименты, доказывающие независимость скорости света от выбора системы отсчёта. В одном из них измерялась скорость фотонов, испущенных распадающейся частицей, которая сама была разогнана почти до половины скорости света. Никаких отличий этой скорости от известного значения скорости света в вакууме обнаружено не было.
В тех же ускорителях частиц отлично наблюдается релятивистское сокращение времени: короткоживущие частицы, разогнанные до высоких скоростей, живут существенно дольше времени, чем «отведено им природой».
Сегодня всерьёз опровергать Специальную теорию относительности могут только откровенные научные фрики. Положения и формулы СТО используются в десятках отраслей современной жизни, от ядерных реакторов до систем спутниковой навигации. И сам тот факт, что эти штуки работают, подтверждает теорию.
Другое дело, что у теории относительности, как и у любой другой теории, существуют свои границы применимости. Так, специальная теория относительности не будет работать в условиях сильных гравитационных полей. Расширить её на эти условия призвана Общая теория относительности. Но об этом – в следующий раз.
Специальная теория относительности Эйнштейна – элементы, формулы кратко и понятно
4.7
Средняя оценка: 4.7
Всего получено оценок: 94.
4.7
Средняя оценка: 4.7
Всего получено оценок: 94.
В конце XIXв представления о пространстве и времени, существующие со времен И.Ньютона, начали входить в противоречие с некоторыми экспериментами.
8$м/с) и одинакова по всем направлениям. А в соответствии с преобразованиями Галилея, если источник электромагнитных волн движется, то скорость распространения электромагнитных волн должна быть больше в направлении движения и меньше в противоположном направлении.
Рис. 1. Электродинамика Фарадея-Максвелла.
Поиск разрешения данного противоречия велся в двух направлениях.
Во-первых, можно предположить, что уравнения электродинамики неверны. Это направление разрабатывал Г. Герц. Он пытался преобразовать уравнения Максвелла так, чтобы они не входили в противоречия с принципом относительности, и правильно описывали скорость света при переходе между инерциальными системами. Такой подход потребовал введения «истиной» Системы Отсчета, относительно которой электродинамика бы описывала все явления.
Во-вторых, можно предположить, что сам принцип относительности не выполняется для механических Систем Отсчета. И здесь также нужна особая, «истинная» Система Отсчета, относительно которой принцип относительности будет справедлив.
Это направление разрабатывалось Х. Лоренцем.
Оба подхода требовали введения «истиной» Системы Отсчета, которая была названа «эфиром», после чего начались его поиски, и попытки определить скорость наблюдателей на Земле относительно эфира.
Опыт Майкельсона
Главным опытом по определению скорости в эфире стал опыт с интерферометром А.Майкельсона. Поскольку свет проходит расстояние «туда и обратно» поперек направления движения Земли быстрее, чем вдоль, эта разница должна фиксироваться по интерференционной картине, причем, картина должна изменяться при изменении ориентации интерферометра.
Рис. 2. Схема опыта Майкельсона.
Однако, многократное повторение опыта показало, что интерференционная картина не зависит от положения интерферометра.
Получалось, что никакого движения относительно эфира нет, а значит, само понятие «эфира» бессмысленно (оно вводилось как раз для объяснения движения относительно других Систем Отсчета).
Постулаты специальной теории относительности
Оставалась единственная возможность «примирить» электродинамику и принцип относительности – согласиться с тем, что они верны, а неверны сами наши представления о пространстве и времени.
В результате А. Эйнштейном была разработана теория, названная Специальной Теорией Относительности (СТО), в основе которой лежат два постулата:
- все процессы и законы (в том числе и законы электродинамики) одинаковы во всех инерциальных Системах Отсчета;
- скорость света в вакууме (с) одинакова для всех инерциальных систем отсчета.
Из этих постулатов следует, что и пространство и время не являются абсолютными, как принято в механике Ньютона, а зависят от Системы Отсчета. Расстояние и время, измеренные в одной Системе, будут отличаться от тех же величин, измеренных в другой. Размеры быстро движущегося тела с точки зрения наблюдателя будут сокращаться. Течение времени для этого тела также будет замедляться.
При этом с точки зрения наблюдателя, находящегося внутри этого тела – все обстоит наоборот. Поскольку тело движется равномерно и прямолинейно, оно является инерциальной Системой Отсчета. А значит, этот наблюдатель может считать, что он покоится, а все остальные предметы быстро движутся.
И именно размеры всех остальных предметов уменьшаются, и время на них замедляется. Размеры и время же этого наблюдателя – остаются прежними.
Подчеркнем – и внешний и движущийся наблюдатель будут правы. Но для согласования результатов их измерений надо использовать не преобразования Галилея, а преобразования Лоренца, формулы которых учитывают скорость движения.
Рис. 3. Преобразования Лоренца.
Что мы узнали?
Изучение элементов Специальной Теории Относительности (СТО) позволяет понять принципы согласования электродинамики Максвелла и механики. В основе СТО лежат постулаты о том, что все процессы во всех Системах Отсчета идут одинаково, и скорость света во всех Системах Отсчета также одинакова. При этом, пространство и время относительны и зависят от скорости наблюдателя.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.
7
Средняя оценка: 4.7
Всего получено оценок: 94.
А какая ваша оценка?
Понимание специальной теории относительности Эйнштейна | Каспер Мюллер | Август 2022 г.
Альберт Эйнштейн — изображение с Викисклада
В этой статье мы обсудим и попытаемся понять одну из самых умопомрачительных теорий, когда-либо написанных. Последствия этих идей и расчетов весьма неинтуитивны, но они вполне реальны.
Я объясню провокационные заявления, такие как:
«Мало того, что путешествия во времени возможны, вы делаете это каждый день, даже не осознавая этого».
И, может быть, даже более нервное:
«Протон содержит больше массы, чем сумма масс всех составляющих его частиц».
Я говорю о теории относительности Эйнштейна. Опубликованная в 1905 году, эта теория полностью перевернула физику, которая уверенно применялась со времен Ньютона и которую до Эйнштейна никто не осмеливался подвергать сомнению.
Наш подход будет , а не , чтобы объяснить, что Эйнштейн сделал в своей статье, а скорее понять свою теорию из тех же фундаментальных принципов и вывести свою эквивалентность массы-энергии E = mc² с минимальным количеством технических средств.
Если вы немного знакомы с основами физики и немного со стандартным исчислением или анализом, все должно быть в порядке. Я постараюсь объяснить концепции по пути, чтобы вы все могли следовать за мной.
Начнем…
Прежде чем погрузиться с головой в уравнения, есть важная вещь, которую, я думаю, должен знать каждый. Когда речь заходит о специальной теории относительности, кажется, что свет возникает совершенно естественно и играет фундаментальную роль во всей теории. Думаю, справедливый вопрос: «Почему свет?».
Интерес представляет не сам свет, а скорость света, и это действительно так. Но не означает ли это, что свет тоже представляет интерес? Что ж, открою вам малоизвестный секрет (по крайней мере, малоизвестный обывателю).
Скорость света не о свете.
Что??! Да, вы правильно прочитали!
Скорость света равна примерно причинно-следственной связи . То есть скорость света на самом деле является пределом космической скорости, с которой информация может путешествовать в нашей Вселенной.
Этот предел космической скорости, который также является скоростью света, равен 299 792 458 м/с .
Фотон (частица света) не имеет массы, и поскольку масса — это единственное, что замедляет вещи во Вселенной, фотон должен двигаться с максимально возможной скоростью, достигая предела космической скорости. Но глюон, например, тоже безмассовый и поэтому тоже движется со скоростью света.
Если бы мы открыли сильное ядерное взаимодействие раньше, чем электромагнитное взаимодействие (что было бы очень странно), то мы бы не назвали предел космической скорости « скорость света », но что-то вроде «скорость сильного взаимодействия» или скорость глюонных волн или что-то в этом роде.
Другой интересный пример — гравитация. Действие силы гравитации движется со скоростью света.
Это означает, что если бы Солнце исчезло сейчас, то в течение следующих 8 минут Земля продолжала бы вращаться вокруг центра нашей Солнечной системы, как если бы Солнце все еще было там, потому что для действия гравитации требуется 8 минут. (и для света), чтобы достичь Земли от Солнца. Через 8 минут Земля больше не будет вращаться вокруг чего-либо, а будет двигаться по прямой линии от Солнечной системы.
На самом деле, из-за этого гипотетическая частица, ответственная за гравитацию (точно так же, как фотон отвечает за силу электромагнетизма, а глюон — за сильное взаимодействие), называемая гравитоном , также должна быть безмассовой. Физики не знают, существует ли он, но ищут его.
Я говорю вам все это, потому что в следующих разделах мы собираемся использовать свет в качестве движущего аргумента, но это только потому, что мысленные эксперименты имеют больше смысла, используя свет, и постулаты относительности сформулированы на этом языке, но вы должны помнить, что в основе всего этого лежит не свет, а причинность.
В начале 20 века у физиков было ньютоновское классическое понимание пространства и времени. Они думали, что пространство статично, а время абсолютно. Это пространство было просто сценой, где разыгрывался грандиозный театр под названием Природа .
У молодого Эйнштейна, работавшего в то время в патентном бюро в Берне, было много свободного времени, чтобы подумать о том, как на самом деле устроена природа. В частности, он много думал о том, что сейчас называют системами отсчета или .инерциальные системы отсчета . Эта идея на самом деле восходит к Gallileo .
В литературе принято объяснять системы отсчета, проводя аналогию с движущимся поездом. Поскольку эта аналогия кажется естественным и цепким выбором, когда дело доходит до объяснения, я не буду менять ее просто ради освежения, поэтому я также расскажу о поезде, но обещаю, что очень скоро все станет очень интересно. .
Прежде чем вместе ехать в поезде, давайте договоримся о так называемом постулате относительности.
Большое озарение Эйнштейна было двояким. Во-первых, когда физическая система (например, камень, человек, поезд и т. д.) движется с постоянной скоростью, то все физические законы в этой системе должны быть такими же, как и все физические законы в любой другой такой системе, движущейся с другой скоростью. постоянная скорость. То есть вы (или физические законы) не можете сказать, движется ли ваша система или движется соседняя система.
Такая система называется инерциальной системой отсчета .
Во-вторых, он понял, что наблюдений, сделанных между двумя такими инерциальными системами отсчета, могут отличаться от наблюдений, сделанных внутри локальной системы, в которой вы находитесь. поезд проходит (вот мы идем). В поезде человек роняет билет. Если вы измерите траекторию этого билета, она будет сильно отличаться от того, если бы ее измерил человек внутри поезда. Очевидно, что для человека в поезде билет упадет по прямой на пол. Но вам кажется, что траектория билета искривлена вбок.
Однако, поскольку физические законы должны быть одинаковыми для систем, и наблюдатель, и человек в поезде должны измерять скорость света одинаково, потому что это фундаментальный закон физики (предел космической скорости, который мы говорили ранее).
Таким образом, в любой инерциальной системе отсчета будут соблюдаться одни и те же законы физики. В частности, скорость света в вакууме всегда измеряется как c , даже при измерении нескольких систем, движущихся с разными постоянными скоростями.
Вот оно! Из этих простых постулатов Эйнштейн смог перевернуть столетия физических знаний. Давайте попробуем разгадать это, выведя знаменитое уравнение E = mc² .
Чтобы использовать только что изложенные принципы относительности, мы собираемся сделать кое-что умное. Мы собираемся построить часы, используя свет. Причина, по которой это разумно, заключается в том, что это позволяет нам сочетать различия в наблюдениях и неизменность скорости света.
Большое осознание Эйнштейна заключалось в том, что если свет всегда движется с одной и той же скоростью, но при определенных обстоятельствах вынужден двигаться на большее расстояние, то есть только одна величина, которая может измениться, и это время . Время нужно замедлить. Чтобы точно рассчитать, сколько, мы проведем небольшой мысленный эксперимент с легкими часами.
Итак, представьте себе два зеркала и световой импульс, идущий туда-сюда между ними. Это аналогия обычному «тиканию» и «так» часов. Рассмотрим следующее изображение.
Image by procrastilearner
Рассматриваемый наблюдатель находится внутри своей собственной инерциальной системы отсчета, поэтому для него применимы часы с левой стороны. Свет прыгает туда-сюда между двумя зеркалами, и он измеряет время, необходимое для перехода света от одного зеркала к другому, которое равно t_0 .
Расстояние между двумя зеркалами определяется как c t_0 . Предположим теперь, что наблюдатель берет в руки большой телескоп и смотрит на другого человека, выполняющего точно такой же эксперимент (с таким же расстоянием между зеркалами) внутри космической ракеты, летящей со скоростью 9.
0019 v (то есть относительно нашего наблюдателя!) .
Очевидно, что для человека в ракете измерения будут точно такими же, как и для нашего наблюдателя, но что увидит наблюдатель, заглянув внутрь ракеты?
Он, конечно, будет наблюдать за светом, движущимся со скоростью света, но в то же время ракета движется со скоростью v , поэтому «тик» и «так» световых часов образуют равнобедренный треугольник. . Высота треугольника будет c t_0 , но время, необходимое свету для достижения второго зеркала, теперь будет c t , где t — наблюдаемое время. За это время ракета прошла v t , что составляет половину основания треугольника.
Равнобедренный треугольник можно представить как объединение двух прямоугольных треугольников. Поэтому теперь мы можем использовать теорему Пифагора для одного из треугольников и написать
, а теперь мы хотим выделить t в этом уравнении. У нас есть
Это потрясающе! С помощью простого мысленного эксперимента мы смогли точно рассчитать, насколько время человека в ракете замедляется по сравнению с нашими часами.
Несколько комментариев по поводу этого результата. Во-первых, это должно быть верно и для любых других часов, поскольку в противном случае можно было бы использовать несоответствие для расчета скорости своей системы отсчета, что нарушило бы первый принцип относительности. Во-вторых, обратите внимание, что если v = 0 , то t = t_0 , что, конечно, имеет смысл. Наши часы идут с той же скоростью, что и любые другие, с той же относительной скоростью, что и наши.
Иногда буква γ вводится как
, так что приведенное выше уравнение становится просто t = γ t_0. Вышеприведенное выражение называется Лоренц фактором и появляется во многих уравнениях относительности.
Что это значит?
Это означает, что чем быстрее вы движетесь, тем медленнее вы движетесь во времени по отношению к наблюдателю. Это может показаться странным, но это действительно так. В крайнем случае, когда вы приближаетесь к скорости света, время полностью останавливается.
Это далеко не все последствия этого. Давайте посмотрим, что это означает для кинетической энергии.
Далее мы используем некоторые физические законы и некоторые вычисления. Чтобы вывод был максимально кратким и лаконичным, я намеренно опустил некоторую строгость. Например, сила, импульс и т. д. на самом деле являются векторами (у них есть величина и направление), но мы будем предполагать, что рассматриваемые функции возвращают действительные числа (поэтому мы можем думать об этом как о длине этих векторов).
Кроме того, если мы хотим проинтегрировать силу вдоль траектории и написать ∫ F dx, мы на самом деле имеем в виду ∫ F(x, t) dx. Вычисления должны иметь смысл, но если читателю нужен более строгий вывод, я уверен, что читатель может выполнить его самостоятельно.
Мало того, что это не очень аккуратно с математической точки зрения, так еще и намеренно отсутствуют некоторые физические аргументы. В конце концов, это не научная статья, и цель здесь — дать понять читателю с ограниченными знаниями.
Таким образом, вы должны рассматривать этот вывод как то, что мы, математики, называем «наброском доказательства», что означает, что вы можете самостоятельно заполнить детали и привести надлежащие аргументы.
Начнем.
Первое, что мы собираемся сделать, это найти кинетическую энергию, получаемую системой при движении из точки x в точку y в пространстве. Чтобы найти кинетическую энергию этой системы, мы можем проинтегрировать силу по отношению к пространству вдоль пути, пройденного системой, т. Е.
. Мы можем представить себе тело, которое сначала находится в состоянии покоя, но затем ускоряется, потому что на него действует сила. Напомним, что классический импульс равен массе, умноженной на скорость, т. е. ρ = m v.
Кроме того, мы знаем, что сила — это скорость изменения импульса, поэтому мы можем записать это как
Небольшой совет. При выполнении таких расчетов и преобразований рекомендуется во время чтения запускать в голове калькулятор размерного анализа.
Например, dρ/dt — это как деление импульса на время, которое в единицах СИ становится (кг ⋅ м/с) / с = кг ⋅ м/с², что, конечно же, является силой. Точно так же следует представить интеграл от F dx как мелкую сумму малых длин, умноженных на силу. Опять же, мы можем проверить, что единицы измерения согласованы кг ⋅ м/с² ⋅ м = кг ⋅ (м/с)², что является энергией.Хорошо. Теперь мы хотим найти релятивистский импульс и решить с его помощью интеграл. К счастью, это не слишком сложно.
Используя цепное правило, мы можем записать импульс как
Таким образом, релятивистский импульс просто имеет дополнительный гамма-фактор, как и релятивистское время. Теперь мы можем подставить это в приведенный выше интеграл, чтобы получить
Обратите внимание, что это можно записать как m d/dt v γ, , и мы попытаемся упростить это выражение. Рассматривая γ как функцию v , мы можем использовать правило произведения для функций f(v) = v и g(v) = γ.
Во-первых, обратите внимание, что по цепному правилу у нас есть
и, следовательно, используя приведенный выше небольшой результат вместе с правилом произведения, мы можем записать
Таким образом, мы можем записать нашу кинетическую энергию в виде следующего интеграла
и отсюда мы просто делаем небольшую замену. Заменяем dv на dx и вносим изменения в пределы интегрирования.
Теперь предположим, что путь, по которому мы интегрируем, имеет начальную скорость 0. Тогда кинетическая энергия при скорости v , начиная с места, становится равной
Здесь последний член исходит из начальной скорости 0, и мы использовали это dx/dt = v . Преобразовывая уравнение, мы получаем
. То есть полная энергия E системы определяется выражением
. Обратите внимание, что если мы установим v = 0, то для покоящегося тела мы получим
, что, конечно же, является знаменитым уравнением Эйнштейна. для энергомассовой эквивалентности покоящегося объекта.
На самом деле, расширяя гамма-фактор Тейлора, мы видим, что
, где, конечно, мы признаем 1/2 м v² как классическую формулу кинетической энергии. Довольно мило.
Последнее, что нам нужно сделать, это вывести отношение энергии-импульса из приведенной выше формулы. Для этого мы просто возводим в квадрат обе части уравнения релятивистского соотношения энергий
и отсюда продолжаем добавлять и вычитать член (m v c γ)² . Таким образом, мы можем записать приведенное выше уравнение в следующем виде
Первый член сводится к м²с⁴ , а второй член — это наш хороший друг, квадрат релятивистского импульса, умноженный на квадрат скорости света. После того, как пыль уляжется, мы получим
Это фантастическая формула. Если рассматриваемая система является безмассовой частицей, то энергия определяется как E = ρ c , а если это система в состоянии покоя, то импульс равен нулю, и уравнение сводится к старому доброму E = m c² .
Мало того, что время является относительным понятием, но с помощью тех же математических аргументов мы можем доказать, что относительно само пространство. То есть и время, и пространство могут быть расширены (сжаты или расширены в зависимости от относительных скоростей между двумя наблюдателями).
Важно понимать, что хотя мы говорим о наблюдениях и что человек внутри движущейся ракеты или поезда не будет испытывать каких-либо странных временных аномалий, последствия этой теории вполне реальны.
Например, если бы вы отправились в космос на ракете, летящей достаточно близко к скорости света в течение года, то, вернувшись, вы бы посетили Землю далеко в будущем. Вы бы раз путешествовали во времени в будущее. Все твои друзья были бы мертвы, но ты был бы всего на год старше, чем был, когда покинул землю.
На самом деле, мы можем использовать уравнения, которые мы только что вывели, чтобы точно рассчитать, как быстро и как долго вам нужно будет путешествовать, чтобы переместиться на x лет в будущее.
Другой пример — тайна мюона. Не вдаваясь в подробности, мюон — это частица (вы можете думать о ней как о толстом родственнике электрона), которая генерируется в большом количестве примерно в 10 километрах от Земли, когда частицы бомбардируются протонами, испускаемыми Солнцем.
Мюоны очень недолговечны. Они распадаются на электроны и нейтрино со средним временем жизни около 2,2 микросекунд, но пока они существуют, они движутся с огромной скоростью. Таким образом, ученые могут рассчитать, используя статистику, сколько из этих толстых электронов должно достичь Земли. Есть только одна проблема. Когда они проводят эксперименты, Земли достигает гораздо больше мюонов, чем должно быть.
Объяснение заключается в том, что поскольку мюоны движутся со скоростью, близкой к скорости света, их «часы» идут намного медленнее, чем наши, и из-за этого замедления времени их период полураспада на наших часах намного дольше, что дает им достаточно времени, чтобы достичь поверхность Земли.
На самом деле, если принять во внимание их разные скорости и теорию относительности, статистика прекрасно согласуется с теорией.
Доводя это до крайности, безмассовая частица, такая как фотон, должна «испытывать» всю историю Вселенной в мгновение ока, потому что для этих частиц вообще нет времени, что бы это ни значило.
Третий пример — загадка протонов с избыточным весом. Масса протона — это больше, чем просто сумма его частей. но как это может быть? Итак, уравнение Эйнштейна говорит нам, что отношение массы покоя частицы к ее энергии всегда постоянно. Следует быть немного осторожным с такими терминами, как релятивистская масса и преобразование между массой и энергией. Это очень тонко. Видите ли, все зависит в первую очередь от того, как мы определяем массу. Мы можем довольно просто определить массу по мере того, как трудно ускорить тело!
Во всяком случае, в определенном смысле уравнение говорит нам, что масса и энергия эквивалентны. Оказывается, протоны состоят из еще более мелких частиц, называемых кварками, и у них есть энергия, но они не покоятся внутри протона.
поэтому из уравнений Эйнштейна мы знаем, что они обладают релятивистской кинетической энергией. Кроме того, глюоны, связывающие протон вместе, обладают энергией (ρ c помните?). Глюоны не только присутствуют, но они также сложным образом взаимодействуют с кварками, давая энергию системе. Вся эта энергия вносит вклад в массу протона.
После разработки этой теории Эйнштейн понял, что она несколько ограничена. Не поймите меня неправильно, это отличная и красивая часть физики сама по себе, но она работала только в особом случае при работе с инерциальными системами отсчета. То есть с постоянными скоростями. Собственно, именно поэтому она и называется специальной теорией относительности. Но реально говоря, объекты во Вселенной почти всегда находятся под действием какой-то силы, действующей на них и придающей им ускорение.
Эйнштейн понял, что ему нужна более общая версия этой теории. Он разработал эту теорию в течение следующих 10 лет. Мы называем это общей теорией относительности.
В общей теории он объясняет эти релятивистские эффекты, когда объекты ускоряются, в том числе объекты в гравитационных полях. Оказывается, эту теорию можно рассматривать как красивый танец между материей и пространством, и что пространство и время на самом деле вплетены в ткань, называемую пространством-временем.
Пространство-время говорит материи, как двигаться; материя сообщает пространству-времени, как искривляться»
~ Джон Уилер
Специальная теория относительности является частным случаем этой более общей теории, поэтому в этой статье мы сделали первый шаг к пониманию общей теории относительности.
Надеюсь, вам понравилась эта статья.
О, и в следующий раз, когда вам будет скучно в машине, поезде или самолете, просто подумайте о том, как вы становитесь моложе, чем были бы, если бы стояли на месте — и теперь вы точно знаете, почему…
Если вам нравится читать подобные статьи на Medium, вы можете оформить членство для полного доступа: просто нажмите здесь .
Спасибо за внимание.
Объяснение теории относительности Эйнштейна за 4 простых шага
Теория относительности Альберта Эйнштейна известна тем, что она предсказала некоторые действительно странные, но верные явления, такие как астронавты стареют медленнее, чем люди на Земле, и твердые объекты, изменяющие свою форму с высокой скоростью.
Но дело в том, что если вы возьмете копию оригинальной статьи Эйнштейна по теории относительности от 1905, это простое чтение. Его текст прост и понятен, а его уравнения в основном состоят из алгебры — ничего такого, что могло бы беспокоить типичного старшеклассника.
Это потому, что Эйнштейн никогда не интересовался сложной математикой. Ему нравилось мыслить визуально, придумывая эксперименты мысленным взором и прокручивая их в голове, пока он не мог видеть идеи и физические принципы с кристальной ясностью. (Прочтите «10 вещей, которые вы (вероятно) не знали об Эйнштейне».)
Чтобы воплотить его процесс в жизнь, National Geographic создала интерактивную версию одного из самых известных мысленных экспериментов Эйнштейна: притчу о ударах молнии, видимых из движущийся поезд, который показывает, как два наблюдателя могут по-разному понимать пространство и время.
Вот как Эйнштейн начал свои мысленные эксперименты, когда ему было всего 16 лет, и как они в конечном итоге привели его к самому революционному уравнению в современной физике.
1895: Бег рядом с лучом света
К этому моменту плохо замаскированное презрение Эйнштейна к жестким, авторитарным методам обучения в его родной Германии уже привело к тому, что его выгнали из эквивалента средней школы, поэтому он переехал в Цюрих в надежде получить учится в Швейцарском федеральном технологическом институте (ETH). (См. также «Почему ФБР хранило 1400-страничный файл об Эйнштейне».)
Однако сначала Эйнштейн решил провести год в школе в соседнем городе Арау — месте, где особое внимание уделялось авангардным методам, таким как независимое мышление и визуализация концепций. В этой счастливой обстановке он вскоре обнаружил, что задается вопросом, каково это — бежать рядом с лучом света.
Эйнштейн уже знал на уроках физики, что такое световой луч: набор колеблющихся электрических и магнитных полей, движущихся со скоростью 186 000 миль в секунду, измеряемой скоростью света.
Если бы он бежал рядом с ним именно с такой скоростью, рассуждал Эйнштейн, он должен был бы быть в состоянии оглянуться и увидеть ряд колеблющихся электрических и магнитных полей, висящих рядом с ним, казалось бы, неподвижных в пространстве.
Но это было невозможно. Во-первых, такие стационарные поля нарушали бы уравнения Максвелла, математические законы, которые систематизировали все, что физики того времени знали об электричестве, магнетизме и свете. Законы были (и остаются) достаточно строгими: любая рябь на полях должна двигаться со скоростью света и не может стоять на месте — без исключений.
Хуже того, стационарные поля не согласуются с принципом относительности, понятием, которое физики приняли со времен Галилея и Ньютона в 17 веке. По сути, теория относительности утверждала, что законы физики не могут зависеть от того, насколько быстро вы движетесь; все, что вы могли измерить, — это скорость одного объекта относительно другого.
Но когда Эйнштейн применил этот принцип к своему мысленному эксперименту, возникло противоречие: теория относительности диктовала, что все, что он может увидеть, двигаясь рядом со световым лучом, включая стационарные поля, также должно быть чем-то, что земные физики могут создать в лаборатории.
Но ничего подобного никогда не наблюдалось.
Эта проблема будет беспокоить Эйнштейна еще 10 лет, на протяжении всей его университетской работы в ETH и его переезда в столицу Швейцарии Берн, где он стал экспертом в швейцарском патентном ведомстве. Вот тут-то он и решил разрешить парадокс раз и навсегда.
1904: Измерение света движущегося поезда
Это было непросто. Эйнштейн перепробовал все возможные решения, но ничего не сработало. Почти в отчаянии он начал обдумывать идею, простую, но радикальную. Может быть, уравнения Максвелла работают для всех, подумал он, но скорость света всегда постоянна.
Другими словами, когда вы видите проносящийся мимо луч света, не имеет значения, движется ли его источник к вам, от вас или в сторону, и не имеет значения, с какой скоростью движется источник. Вы всегда будете измерять скорость этого луча как 186 000 миль в секунду. Помимо прочего, это означало, что Эйнштейн никогда не увидит стационарных колеблющихся полей, потому что он никогда не сможет поймать световой луч.
Это был единственный способ, которым Эйнштейн мог примирить уравнения Максвелла с принципом относительности. Однако поначалу казалось, что у этого решения есть свой фатальный недостаток. Позже Эйнштейн объяснил эту проблему с помощью другого мысленного эксперимента: представьте, что луч света пускается вдоль железнодорожной насыпи в тот момент, когда поезд с ревом мчится в том же направлении со скоростью, скажем, 2000 миль в секунду.
Кто-нибудь, стоящий на набережной, измерил бы скорость светового луча как стандартное число, 186 000 миль в секунду. Но кто-нибудь в поезде увидит, как он движется со скоростью всего 184 000 миль в секунду. Если бы скорость света не была постоянной, уравнения Максвелла должны были бы каким-то образом выглядеть внутри железнодорожного вагона, заключал Эйнштейн, и принцип относительности был бы нарушен.
Это кажущееся противоречие заставило Эйнштейна почти год крутить колеса. Но затем, прекрасным майским утром 1905 года, он шел на работу со своим лучшим другом Микеле Бессо, инженером, которого он знал еще со студенческих времен в Цюрихе.
Двое мужчин говорили о дилемме Эйнштейна, как они часто делали. И вдруг Эйнштейн увидел решение. Он работал над ним всю ночь, а когда они встретились на следующее утро, Эйнштейн сказал Бессо: «Спасибо. Я полностью решил проблему».
Май 1905: Молния поражает движущийся поезд
Открытие Эйнштейна состояло в том, что наблюдатели в относительном движении воспринимают время по-разному: вполне возможно, что два события происходят одновременно с точки зрения одного наблюдателя, но происходят в разное время с точки зрения другого. Другой. И оба наблюдателя будут правы.
Эйнштейн позже проиллюстрировал это положение еще одним мысленным экспериментом. Представьте, что вы снова видите наблюдателя, стоящего на железнодорожной насыпи, когда мимо с ревом проносится поезд. Но на этот раз в каждый конец поезда ударяет молния как раз в тот момент, когда поезд проходит середину. Поскольку удары молнии находятся на одинаковом расстоянии от наблюдателя, их свет достигает его глаза в одно и то же мгновение.
Так что он правильно говорит, что они произошли одновременно.
Тем временем другой наблюдатель в поезде сидит ровно посередине. С ее точки зрения, свет от двух ударов также должен пройти равные расстояния, и она также будет измерять скорость света одинаковой в любом направлении. Но поскольку поезд движется, свет, исходящий от молнии сзади, должен пройти большее расстояние, чтобы догнать ее, поэтому он достигает ее на несколько мгновений позже, чем свет, исходящий спереди. Поскольку световые импульсы пришли в разное время, она может только заключить, что ударов было 9.0355, а не одновременно — что то, что впереди, на самом деле произошло первым.
Короче говоря, понял Эйнштейн, одновременность — это то, что относительно. Как только вы примете это, все странные эффекты, которые мы теперь связываем с теорией относительности, станут вопросом простой алгебры.
Эйнштейн лихорадочно изложил свои идеи и всего через несколько недель отправил свою статью для публикации.
Он дал ей название — «Об электродинамике движущихся тел», — что говорило о его борьбе за примирение уравнений Максвелла с принципом относительности. И в заключение он поблагодарил Бессо («Я обязан ему несколькими ценными предложениями»), что гарантировало его другу прикосновение бессмертия.
Сентябрь 1905: Масса и Энергия
Тем не менее, первая статья не была концом. Эйнштейн был одержим теорией относительности все лето 1905 года, а в сентябре прислал вторую статью как своего рода запоздалую мысль.
Он был основан на еще одном мысленном эксперименте. «Представьте объект, который находится в состоянии покоя», — сказал он. А теперь представьте, что он спонтанно испускает два одинаковых световых импульса в противоположных направлениях. Объект останется на месте, но поскольку каждый импульс уносит определенное количество энергии, энергоемкость объекта будет уменьшаться.
Теперь, сказал Эйнштейн, как бы выглядел этот процесс для движущегося наблюдателя? С ее точки зрения, объект просто продолжал двигаться по прямой линии, в то время как два импульса расходились.
Но даже если скорость двух импульсов осталась бы одинаковой — скоростью света, — их энергии были бы разными: импульс, движущийся вперед в направлении движения, теперь имел бы более высокую энергию, чем импульс, движущийся назад.
Приложив немного больше алгебры, Эйнштейн показал, что для того, чтобы все это было непротиворечивым, объект должен не только терять энергию при выходе световых импульсов, но и немного терять массу. Или, другими словами, масса и энергия взаимозаменяемы.
Эйнштейн записал уравнение, связывающее их. Используя сегодняшние обозначения, в которых скорость света сокращается с помощью буквы c , он легко вывел самое известное из когда-либо написанных уравнений: E = mc 2 .
Читать дальше
Знакомство с последними каменщиками соборов Англии
- Путешествия
Знакомство с последними каменщиками соборов Англии
Работа каменщика далеко не одномерна.
Эксклюзивный контент для подписчиков
Почему люди так одержимы Марсом?
Как вирусы формируют наш мир
Эпоха собачьих бегов в США подходит к концу будет исследовать красную планету
Почему люди так одержимы Марсом?
Как вирусы формируют наш мир
Эпоха собачьих бегов в США подходит к концу
Узнайте, как люди представляли себе жизнь на Марсе на протяжении истории будет исследовать красную планету
Почему люди так одержимы Марсом?
Как вирусы формируют наш мир
Эпоха собачьих бегов в США подходит к концу
Узнайте, как люди представляли себе жизнь на Марсе на протяжении всей истории
Узнайте, как новый марсоход НАСА будет исследовать красную планету
Подробнее
Гравитация как геометрия | Общая теория относительности: краткое введение
Фильтр поиска панели навигации
Oxford AcademicОбщая теория относительности: краткое введениеАстрономия и астрофизикаВычислительная физикаМатематическая и статистическая физикаКнигиЖурналы
Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации
Oxford AcademicОбщая теория относительности: краткое введениеАстрономия и астрофизикаВычислительная физикаМатематическая и статистическая физикаКнигиЖурналы
Термин поиска на микросайте
Расширенный поиск
Иконка Цитировать
ЦитироватьРазрешения
Делиться
- Твиттер
- Еще
Ссылка
Carlip, Steven,
‘Gravity as geometry’
,
General Relativity: A Concise Introduction
(
Oxford,
2019;
online edn,
Oxford Academic
, 21 Mar.
2019
), https://doi.org/10.1093/oso/9780198822158.003.0001,
, по состоянию на 7 октября 2022 г.
Выберите формат
Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)
Закрыть
Фильтр поиска панели навигации
Oxford AcademicОбщая теория относительности: краткое введениеАстрономия и астрофизикаВычислительная физикаМатематическая и статистическая физикаКнигиЖурналы
Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации
Oxford AcademicОбщая теория относительности: краткое введениеАстрономия и астрофизикаВычислительная физикаМатематическая и статистическая физикаКнигиЖурналы
Термин поиска на микросайте
Advanced Search
Abstract
Общая теория относительности описывает гравитацию как побочный продукт геометрии пространства-времени.
В этой главе объясняется, почему это понятие имеет смысл, и вводится принцип эквивалентности и универсальности гравитационных взаимодействий.
Ключевые слова:
общая теория относительности, гравитация, теорема Остроградского, принцип эквивалентности, геометрия пространства-времени
Предмет
Астрономия и астрофизикаМатематическая и статистическая физикаВычислительная физика
В настоящее время у вас нет доступа к этой главе.
Войти
Получить помощь с доступом
Получить помощь с доступом
Доступ для учреждений
Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Доступ на основе IP
Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов.
Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.
Войдите через свое учреждение
Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.
- Нажмите Войти через свое учреждение.
- Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
- Находясь на сайте учреждения, используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.
Войти с помощью читательского билета
Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Члены общества
Доступ члена общества к журналу достигается одним из следующих способов:
Войти через сайт сообщества
Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
- Щелкните Войти через сайт сообщества.
- При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.
Вход через личный кабинет
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже.
Личный кабинет
Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.
Просмотр ваших зарегистрированных учетных записей
Щелкните значок учетной записи в правом верхнем углу, чтобы:
- Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.
- Просмотр институциональных учетных записей, предоставляющих доступ.
Выполнен вход, но нет доступа к содержимому
Oxford Academic предлагает широкий ассортимент продукции.