Просто о квантовой запутанности / Хабр
Квантовая запутанность – одно из самых сложных понятий в науке, но основные её принципы просты. А если понять её, запутанность открывает путь к лучшему пониманию таких понятий, как множественность миров в квантовой теории.
Чарующей аурой загадочности окутано понятие квантовой запутанности, а также (каким-то образом) связанное с ним требование квантовой теории о необходимости наличия «многих миров». И, тем не менее, по сути своей это научные идеи с приземлённым смыслом и конкретными применениями. Я хотел бы объяснить понятия запутанности и множества миров настолько просто и ясно, насколько знаю их сам.
I
Запутанность считается явлением, уникальным для квантовой механики – но это не так. На самом деле, для начала будет более понятным (хотя это и необычный подход) рассмотреть простую, не квантовую (классическую) версию запутанности. Это позволит нам отделить тонкости, связанные с самой запутанностью, от других странностей квантовой теории.
Запутанность появляется в ситуациях, в которых у нас есть частичная информация о состоянии двух систем. К примеру, нашими системами могут стать два объекта – назовём их каоны. «К» будет обозначать «классические» объекты. Но если вам очень хочется представлять себе что-то конкретное и приятное – представьте, что это пирожные.
Наши каоны будут иметь две формы, квадратную или круглую, и эти формы будут обозначать их возможные состояния. Тогда четырьмя возможными совместными состояниями двух каонов будут: (квадрат, квадрат), (квадрат, круг), (круг, квадрат), (круг, круг). В таблице указана вероятность нахождения системы в одном из четырёх перечисленных состояний.
Мы будем говорить, что каоны «независимы», если знание о состоянии одного из них не даёт нам информации о состоянии другого. И у этой таблицы есть такое свойство. Если первый каон (пирожное) квадратный, мы всё ещё не знаем форму второго. И наоборот, форма второго ничего не говорит нам о форме первого.
С другой стороны, мы скажем, что два каона запутаны, если информация об одном из них улучшает наши знания о другом. Вторая табличка покажет нам сильную запутанность. В этом случае, если первый каон будет круглым, мы будем знать, что второй тоже круглый. А если первый каон квадратный, то таким же будет и второй. Зная форму одного, мы однозначно определим форму другого.
Вторая табличка покажет нам сильную запутанность. В этом случае, если первый каон будет круглым, мы будем знать, что второй тоже круглый. А если первый каон квадратный, то таким же будет и второй. Зная форму одного, мы однозначно определим форму другого.
Квантовая версия запутанности выглядит, по сути, также – это отсутствие независимости. В квантовой теории состояния описываются математическими объектами под названием волновая функция. Правила, объединяющие волновые функции с физическими возможностями, порождают очень интересные сложности, которые мы обсудим позже, но основное понятие о запутанном знании, которое мы продемонстрировали для классического случая, остаётся тем же.
Хотя пирожные нельзя считать квантовыми системами, запутанность квантовых систем возникает естественным путём – например, после столкновений частиц. На практике незапутанные (независимые) состояния можно считать редкими исключениями, поскольку при взаимодействии систем между ними возникают корреляции.
Рассмотрим, к примеру, молекулы. Они состоят из подсистем – конкретно, электронов и ядер. Минимальное энергетическое состояние молекулы, в котором она обычно и находится, представляет собой сильно запутанное состояние электронов и ядра, поскольку расположение этих составляющих частиц никак не будет независимым. При движении ядра электрон движется с ним.
Вернёмся к нашему примеру. Если мы запишем Φ■, Φ● как волновые функции, описывающие систему 1 в её квадратных или круглых состояниях и ψ■, ψ● для волновых функций, описывающих систему 2 в её квадратных или круглых состояниях, тогда в нашем рабочем примере все состояния можно описать, как:
Независимые: Φ■ ψ■ + Φ■ ψ● + Φ● ψ■ + Φ● ψ●
Запутанные: Φ■ ψ■ + Φ● ψ●
Независимую версию также можно записать, как:
(Φ■ + Φ●)(ψ■ + ψ●)
Отметим, как в последнем случае скобки чётко разделяют первую и вторую системы на независимые части.
Существует множество способов создания запутанных состояний. Один из них – измерить составную систему, дающую вам частичную информацию.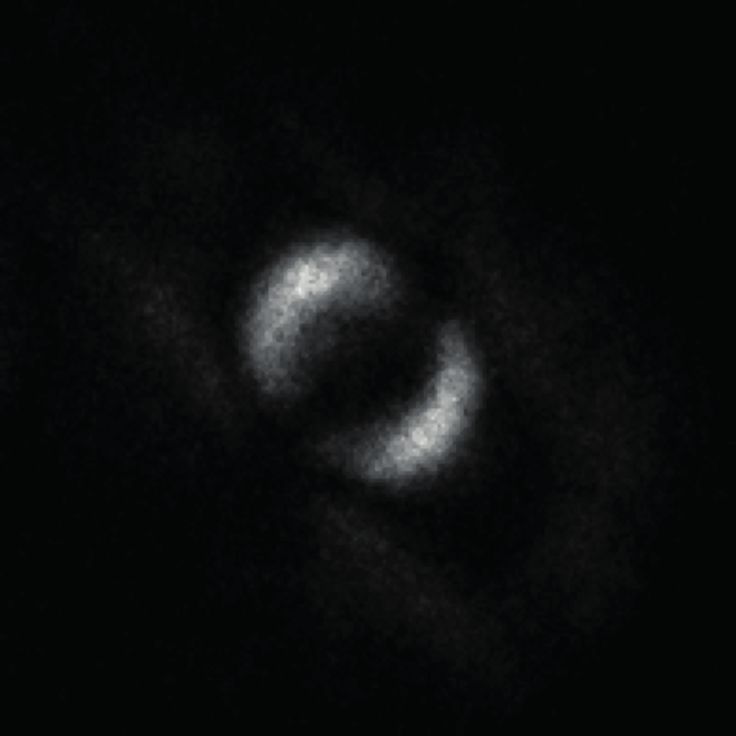 Можно узнать, например, что две системы договорились быть одной формы, не зная при этом, какую именно форму они выбрали. Это понятие станет важным чуть позже.
Можно узнать, например, что две системы договорились быть одной формы, не зная при этом, какую именно форму они выбрали. Это понятие станет важным чуть позже.
Более характерные последствия квантовой запутанности, такие, как эффекты Эйнштейна-Подольского-Розена (EPR) и Гринберга-Хорна-Зейлингера (GHZ), возникают из-за её взаимодействия ещё с одним свойством квантовой теории под названием «принцип дополнительности». Для обсуждения EPR и GHZ позвольте мне сначала представить вам этот принцип.
До этого момента мы представляли, что каоны бывают двух форм (квадратные и круглые). Теперь представим, что ещё они бывают двух цветов – красного и синего. Рассматривая классические системы, например, пирожные, это дополнительное свойство означало бы, что каон может существовать в одном из четырёх возможных состояний: красный квадрат, красный круг, синий квадрат и синий круг.
Но квантовые пирожные – квантожные… Или квантоны… Ведут себя совсем по-другому. То, что квантон в каких-то ситуациях может обладать разной формой и цветом не обязательно означает, что он одновременно обладает как формой, так и цветом. Фактически, здравый смысл, которого требовал Эйнштейн от физической реальности, не соответствует экспериментальным фактам, что мы скоро увидим.
Фактически, здравый смысл, которого требовал Эйнштейн от физической реальности, не соответствует экспериментальным фактам, что мы скоро увидим.
Мы можем измерить форму квантона, но при этом мы потеряем всю информацию о его цвете. Или мы можем измерить цвет, но потеряем информацию о его форме. Согласно квантовой теории, мы не можем одновременно измерить и форму и цвет. Ничей взгляд на квантовую реальность не обладает полнотой; приходится принимать во внимание множество разных и взаимоисключающих картин, у каждой из которых есть своё неполное представление о происходящем. Это и есть суть принципа дополнительности, такая, как её сформулировал Нильс Бор.
В результате квантовая теория заставляет нас быть осмотрительными в приписывании свойствам физической реальности. Во избежание противоречий приходится признать, что:
Не существует свойства, если его не измерили.
Измерение – активный процесс, изменяющий измеряемую систему
II
Теперь опишем две образцовые, но не классические, иллюстрации странностей квантовой теории. Обе были проверены в строгих экспериментах (в реальных экспериментах люди меряют не формы и цвета пирожных, а угловые моменты электронов).
Обе были проверены в строгих экспериментах (в реальных экспериментах люди меряют не формы и цвета пирожных, а угловые моменты электронов).
Альберт Эйнштейн, Борис Подольский и Натан Розен (EPR) описали удивительный эффект, возникающий при запутанности двух квантовых систем. EPR-эффект объединяет особую, экспериментально достижимую форму квантовой запутанности с принципом дополнительности.
EPR-пара состоит из двух квантонов, у каждого из которых можно измерить форму или цвет (но не то и другое сразу). Предположим, что у нас есть множество таких пар, все они одинаковые, и мы можем выбирать, какие измерения мы проводим над их компонентами. Если мы измерим форму одного из членов EPR-пары, мы с одинаковой вероятностью получим квадрат или круг. Если измерим цвет, то с одинаковой вероятностью получим красный или синий.
Интересные эффекты, казавшиеся EPR парадоксальными, возникают, когда мы проводим измерения обоих членов пары. Когда мы меряем цвет обоих членов, или их форму, мы обнаруживаем, что результаты всегда совпадают. То есть, если мы обнаружим, что один из них красный и затем меряем цвет второго, мы также обнаруживаем, что он красный – и т.п. С другой стороны, если мы измеряем форму одного и цвет другого, никакой корреляции не наблюдается. То есть, если первый был квадратом, то второй с одинаковой вероятностью может быть синим или красным.
То есть, если мы обнаружим, что один из них красный и затем меряем цвет второго, мы также обнаруживаем, что он красный – и т.п. С другой стороны, если мы измеряем форму одного и цвет другого, никакой корреляции не наблюдается. То есть, если первый был квадратом, то второй с одинаковой вероятностью может быть синим или красным.
Согласно квантовой теории, мы получим такие результаты, даже если две системы будет разделять огромное расстояние и измерения будут проведены почти одновременно. Выбор типа измерений в одном месте, судя по всему, влияет на состояние системы в другом месте. Это «пугающее дальнодействие», как называл его Эйнштейн, по-видимому, требует передачу информации – в нашем случае, информации о проведённом измерении – со скоростью, превышающей скорость света.
Но так ли это? Пока я не узнаю, какой результат получили вы, я не знаю, чего ожидать мне. Я получаю полезную информацию, когда я узнаю ваш результат, а не когда вы проводите измерение. И любое сообщение, содержащее полученный вами результат, необходимо передать каким-либо физическим способом, медленнее скорости света.
При дальнейшем изучении парадокс ещё больше разрушается. Давайте рассмотрим состояние второй системы, если измерение первой дало красный цвет. Если мы решим мерить цвет второго квантона, мы получим красный. Но по принципу дополнительности, если мы решим измерить его форму, когда он находится в «красном» состоянии, у нас будут равные шансы на получение квадрата или круга. Поэтому, результат EPR логически предопределён. Это просто пересказ принципа дополнительности.
Нет парадокса и в том, что удалённые события коррелируют. Ведь если мы положим одну из двух перчаток из пары в коробки и отправим их в разные концы планеты, неудивительно, что посмотрев в одну коробку, я могу определить, на какую руку предназначена другая перчатка. Точно так же, во всех случаях корреляция пар EPR должна быть зафиксирована на них, когда они находятся рядом и потому они могут выдержать последующее разделение, будто бы имея память. Странность EPR-парадокса не в самой по себе возможности корреляции, а в возможности её сохранения в виде дополнений.
III
Дэниел Гринбергер, Майкл Хорн и Антон Зейлингер открыли ещё один прекрасный пример квантовой запутанности. ОН включает три наших квантона, находящихся в специально подготовленном запутанном состоянии (GHZ-состоянии). Мы распределяем каждый из них разным удалённым экспериментаторам. Каждый из них выбирает, независимо и случайно, измерять ли цвет или форму и записывает результат. Эксперимент повторяют многократно, но всегда с тремя квантонами в GHZ-состоянии.
Каждый отдельно взятый экспериментатор получает случайные результаты. Измеряя форму квантона, он с равной вероятностью получает квадрат или круг; измеряя цвет квантона, он с равной вероятностью получает красный или синий. Пока всё обыденно.
Но когда экспериментаторы собираются вместе и сравнивают результаты, анализ показывает удивительный результат. Допустим, мы будем называть квадратную форму и красный цвет «добрыми», а круги и синий цвет – «злыми». Экспериментаторы обнаруживают, что если двое из них решили измерить форму, а третий – цвет, тогда либо 0, либо 2 результата измерений получаются «злыми» (т. е. круглыми или синими). Но если все трое решают измерить цвет, то либо 1 либо 3 измерения получаются злыми. Это предсказывает квантовая механика, и именно это и происходит.
е. круглыми или синими). Но если все трое решают измерить цвет, то либо 1 либо 3 измерения получаются злыми. Это предсказывает квантовая механика, и именно это и происходит.
Вопрос: количество зла чётное или нечётное? В разных измерениях реализовываются обе возможности. Нам приходится отказаться от этого вопроса. Не имеет смысла рассуждать о количестве зла в системе без связи с тем, как его измеряют. И это приводит к противоречиям.
Эффект GHZ, как описывает его физик Сидни Колман, это «оплеуха от квантовой механики». Он разрушает привычное, полученное из опыта ожидание того, что у физических систем есть предопределённые свойства, независимые от их измерения. Если бы это было так, то баланс доброго и злого не зависел бы от выбора типов измерений. После того, как вы примете существование GHZ-эффекта, вы его не забудете, а ваш кругозор будет расширен.
IV
Пока что мы рассуждаем о том, как запутанность не позволяет назначить уникальные независимые состояния нескольким квантонам. Такие же рассуждения применимы к изменениям одного квантона, происходящим со временем.
Такие же рассуждения применимы к изменениям одного квантона, происходящим со временем.
Мы говорим об «запутанных историях», когда системе невозможно присвоить определённое состояние в каждый момент времени. Так же, как в традиционной запутанности мы исключаем какие-то возможности, мы можем создать и запутанные истории, проводя измерения, собирающие частичную информацию о прошлых событиях. В простейших запутанных историях у нас есть один квантон, изучаемый нами в два разных момента времени. Мы можем представить ситуацию, когда мы определяем, что форма нашего квантона оба раза была квадратной, или круглой оба раза, но при этом остаются возможными обе ситуации. Это темпоральная квантовая аналогия простейшим вариантам запутанности, описанным ранее.
Используя более сложный протокол, мы можем добавить чуть-чуть дополнительности в эту систему, и описать ситуации, вызывающие «многомировое» свойство квантовой теории. Наш квантон можно подготовить в красном состоянии, а затем измерить и получить голубое. И как в предыдущих примерах, мы не можем на постоянной основе присвоить квантону свойство цвета в промежутке между двумя измерениями; нет у него и определённой формы. Такие истории реализовывают, ограниченным, но полностью контролируемым и точным способом, интуицию, свойственную картинке множественности миров в квантовой механике. Определённое состояние может разделиться на две противоречащие друг другу исторические траектории, которые затем снова соединяются.
И как в предыдущих примерах, мы не можем на постоянной основе присвоить квантону свойство цвета в промежутке между двумя измерениями; нет у него и определённой формы. Такие истории реализовывают, ограниченным, но полностью контролируемым и точным способом, интуицию, свойственную картинке множественности миров в квантовой механике. Определённое состояние может разделиться на две противоречащие друг другу исторические траектории, которые затем снова соединяются.
Эрвин Шрёдингер, основатель квантовой теории, скептически относившийся к её правильности, подчёркивал, что эволюция квантовых систем естественным образом приводит к состояниям, измерение которых может дать чрезвычайно разные результаты. Его мысленный эксперимент с «котом Шрёдингера» постулирует, как известно, квантовую неопределённость, выведенную на уровень влияния на смертность кошачьих. До измерения коту невозможно присвоить свойство жизни (или смерти). Оба, или ни одно из них, существуют вместе в потустороннем мире возможностей.
Повседневный язык плохо приспособлен для объяснения квантовой дополнительности, в частности потому, что повседневный опыт её не включает. Практические кошки взаимодействуют с окружающими молекулами воздуха, и другими предметами, совершенно по-разному, в зависимости от того, живы они или мертвы, поэтому на практике измерение проходит автоматически, и кот продолжает жить (или не жить). Но истории с запутанностью описывают квантоны, являющиеся котятами Шрёдингера. Их полное описание требует, чтобы мы принимали к рассмотрению две взаимоисключающие траектории свойств.
Контролируемая экспериментальная реализация запутанных историй – вещь деликатная, поскольку требует сбора частичной информации о квантонах. Обычные квантовые измерения обычно собирают всю информацию сразу – к примеру, определяют точную форму или точный цвет – вместо того, чтобы несколько раз получить частичную информацию. Но это можно сделать, хотя и с чрезвычайными техническими трудностями. Этим способом мы можем присвоить определённый математический и экспериментальный смысл распространению концепции «множественности миров» в квантовой теории, и продемонстрировать её реальность.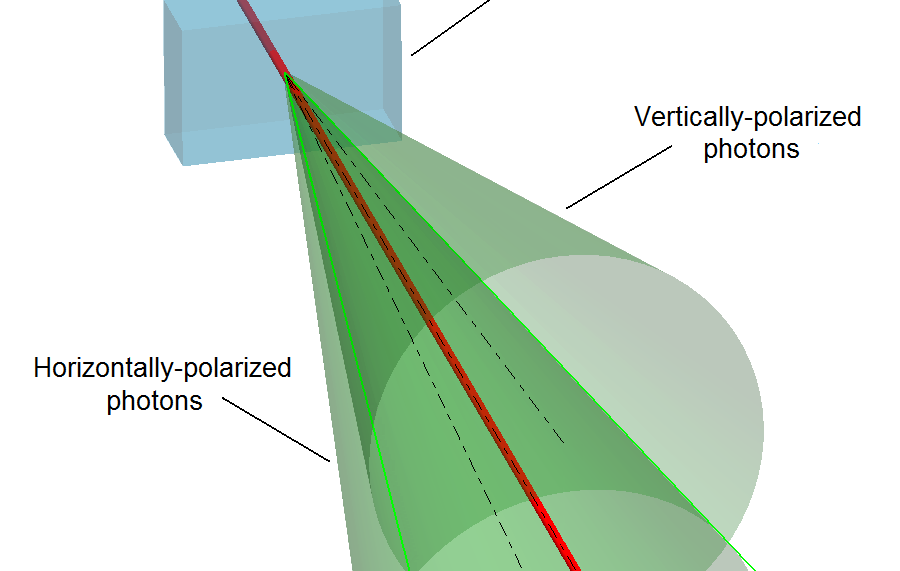
Физики сфотографировали квантовую запутанность
Шотландские ученые получили первое в мире изображение запутанных фотонов в момент неопределенности их физических состояний. Исследование опубликовано в Science Advances.
Квантовая запутанность — феномен, при котором квантовые состояния нескольких частиц оказываются взаимосвязанными вне зависимости от расстояния между ними. Это явление применяется в квантовой телепортации, криптографии и компьютерных технологиях. Эйнштейн с коллегами показали, что если квантовая механика полностью бы отражала реальность, то знания о состоянии одной части запутанной системы автоматически определяют состояние другой части. Получается, что информация в таком случае передается быстрее скорости света, что невозможно по законам классической физики.
В квантовой механике частицы одновременно являются и волнами без определенного положения в пространстве. Только когда появляется наблюдатель, системе приходится принять одно определенное квантовое состояние. Запутанные же частицы влияют на выбор состояния друг друга, даже если между ними больше тысячи километров.
Запутанные же частицы влияют на выбор состояния друг друга, даже если между ними больше тысячи километров.
От редактора
Наш читатель Марат Хамадеев в комментариях в социальных сетях подчеркнул необходимость обратить внимание на саму значимость работы.
Экспериметально доказать квантовую запутанность частиц можно проверив выполнение неравенств Белла, которые предполагают наличие скрытых параметров, определяющих состояние, которое примет одна из частиц, и результаты эксперимента можно предсказать. В том случае, если они не выполняются, частицы можно считать запутанными.
Эксперименты, которые доказали нарушение неравенств Белла уже не раз проводили, в основном проверяя соответсвие поляризаций фотонов, но иногда и со спинами электронов. В настоящей работе ученым удалось собрать установку для призрачной визуализации доказательства нарушения неравенств по орбитальным угловым моментам фотонов закрученного света.
Поль-Антуан Моро (Paul-Antoine Moreau) с коллегами из Университета Глазго разделили пары запутанных фотонов, один направили сквозь жидкий кристалл, который играл роль пространственного модулятора света и изменял фазу фотонов, а другой — сразу на детектор.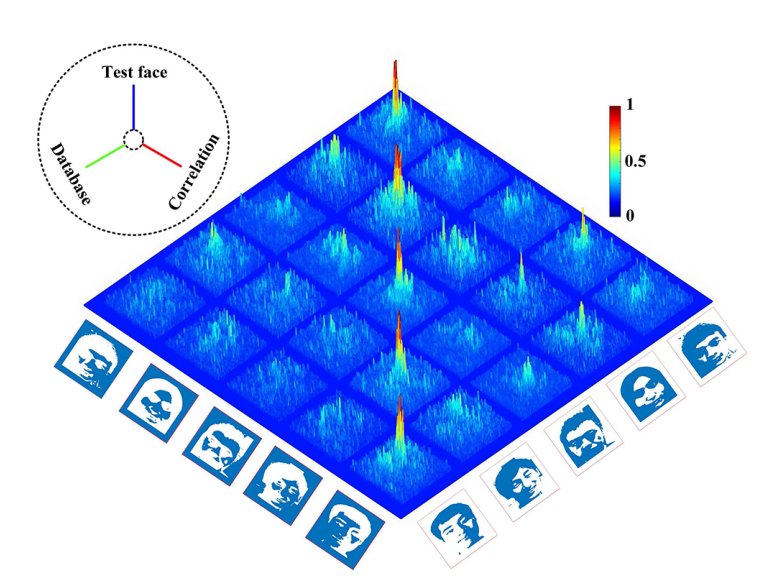 Камера зафиксировала изображения всех фотонов в момент, когда они претерпевали одни и те же превращения, хотя и были разделены в пространстве. То есть в момент квантовой запутанности.
Камера зафиксировала изображения всех фотонов в момент, когда они претерпевали одни и те же превращения, хотя и были разделены в пространстве. То есть в момент квантовой запутанности.
Сверхчувствительная камера была способна фиксировать единичные фотоны и делать снимки только в тот момент, когда на детекторы попадала пара запутанных фотонов. Помимо четырех отдельных изображений пар, которые проходили через четыре разных фильтра, авторы работы получили одну фотографию со всеми четырьмя вариантами изменения фазы.
Результаты эксперимента подтолкнут развитие технологий получения изображений квантовых явлений, что в свою очередь, приблизит ученых к пониманию этих процессов и их дальнейшему применению.
Хотя запутанность уже используется в квантовых технологиях, изображение этого эффекта ученые получили впервые. Однако увидеть невооруженным глазом квантово-запутанные частицы уже было можно, когда физики предложили схему такого эксперимента.
Алина Кротова
Нашли опечатку? Выделите фрагмент и нажмите Ctrl+Enter.
запутанных фотонов теперь могут выходить в сети
Борьба, с которой сталкивается большинство компаний при поддержке кода, вызывает вторую проблему: хрупкость. Каждая новая функция, добавляемая в код, увеличивает его сложность, что увеличивает вероятность того, что что-то сломается. Обычно программное обеспечение становится настолько сложным, что разработчики избегают вносить в него изменения больше, чем это абсолютно необходимо, опасаясь что-то сломать. Во многих компаниях целые команды разработчиков работают не для того, чтобы разрабатывать что-то новое, а просто для того, чтобы поддерживать существующие системы в рабочем состоянии. Можно сказать, что они используют версию программного обеспечения
Гонка Красной Королевы, которая бежит так быстро, как только может, лишь бы остаться на одном месте.
Это печальная ситуация. Тем не менее, текущая траектория индустрии программного обеспечения направлена на увеличение сложности, увеличение времени разработки продукта и повышение хрупкости производственных систем. Для решения таких проблем компании обычно просто привлекают к решению проблемы больше людей: больше разработчиков, больше тестировщиков и больше техников, которые вмешиваются, когда системы выходят из строя.
Для решения таких проблем компании обычно просто привлекают к решению проблемы больше людей: больше разработчиков, больше тестировщиков и больше техников, которые вмешиваются, когда системы выходят из строя.
Наверняка должен быть лучший способ. Я являюсь частью растущей группы разработчиков, которые считают, что ответом может быть функциональное программирование. Здесь я описываю, что такое функциональное программирование, почему его использование помогает и почему я так им увлечен.
При функциональном программировании меньше значит больше
Хороший способ понять
обоснование функционального программирования заключается в рассмотрении того, что произошло более полувека назад. В конце 1960-х возникла парадигма программирования, направленная на повышение качества кода при одновременном сокращении необходимого времени разработки. Это называлось структурным программированием.
Появились различные языки для поддержки структурированного программирования, а некоторые существующие языки были изменены для лучшей его поддержки. Одной из самых примечательных особенностей этих языков структурного программирования было вовсе не свойство: это было отсутствие чего-то, что существовало долгое время —
Одной из самых примечательных особенностей этих языков структурного программирования было вовсе не свойство: это было отсутствие чего-то, что существовало долгое время —
оператор GOTO.
Оператор GOTO используется для перенаправления выполнения программы. Вместо выполнения следующего оператора по порядку поток программы перенаправляется на какой-то другой оператор, указанный в строке GOTO, обычно при выполнении некоторого условия.
Исключение GOTO было основано на том, что программисты узнали из его использования — что это сделало программу очень трудной для понимания. Программы с GOTO часто называли спагетти-кодом, потому что последовательность выполняемых инструкций могла быть такой же сложной, как одна нить в миске со спагетти.
Шира Инбар
Неспособность этих разработчиков понять, как работает их код или почему он иногда не работает, была проблемой сложности. Эксперты по программному обеспечению той эпохи считали, что эти операторы GOTO
создавали ненужную сложность, и что GOTO должен был уйти.
В то время это была радикальная идея, и многие программисты сопротивлялись потере утверждения, на которое они привыкли полагаться. Споры продолжались более десяти лет, но, в конце концов, GOTO угасла, и сегодня никто не стал бы выступать за ее возвращение. Это связано с тем, что его исключение из языков программирования более высокого уровня значительно снизило сложность и повысило надежность создаваемого программного обеспечения. Это было сделано за счет ограничения того, что могли делать программисты, что в конечном итоге облегчило им анализ кода, который они писали.
Хотя индустрия программного обеспечения исключила GOTO из современных языков высокого уровня, программное обеспечение, тем не менее, продолжает становиться все более сложным и хрупким. В поисках того, как еще можно модифицировать такие языки программирования, чтобы избежать некоторых распространенных ошибок, разработчики программного обеспечения могут, как ни странно, черпать вдохновение у своих коллег на аппаратной стороне.
Обнуление проблем с нулевыми ссылками
При проектировании оборудования
для компьютера у вас не может быть общего резистора, скажем, для клавиатуры и схемы монитора. Но программисты все время делают такой обмен в своем программном обеспечении. Это называется общим глобальным состоянием: переменные не принадлежат ни одному процессу, но могут быть изменены любым количеством процессов, даже одновременно.
Теперь представьте, что каждый раз, когда вы запускаете микроволновую печь, настройки посудомоечной машины менялись с обычного цикла на кастрюли и сковородки. Такого, конечно, не происходит в реальном мире, но в программном обеспечении такое происходит постоянно. Программисты пишут код, который вызывает функцию, ожидая, что она выполнит одну задачу. Но у многих функций есть побочные эффекты, которые изменяют общее глобальное состояние,
приводя к неожиданным последствиям.
В аппаратном обеспечении этого не происходит, потому что законы физики ограничивают возможности.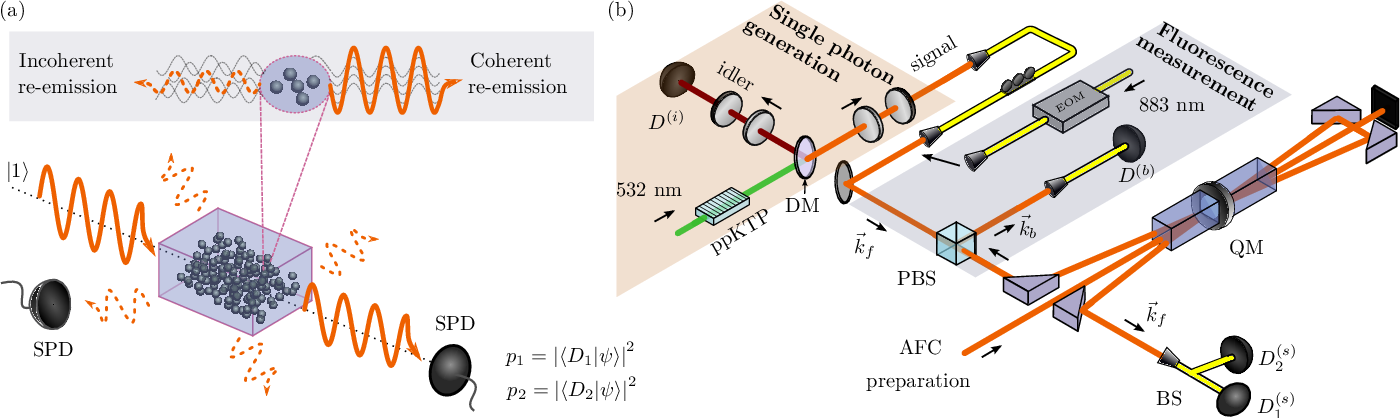 Конечно, инженеры по аппаратному обеспечению могут ошибаться, но не так, как вы можете с программным обеспечением, где слишком многое возможно, к лучшему или к худшему.
Конечно, инженеры по аппаратному обеспечению могут ошибаться, но не так, как вы можете с программным обеспечением, где слишком многое возможно, к лучшему или к худшему.
Еще один монстр сложности, скрывающийся в трясине программного обеспечения, называется
нулевая ссылка, означающая, что ссылка на место в памяти вообще ни на что не указывает. Если вы попытаетесь использовать эту ссылку, произойдет ошибка. Таким образом, программисты должны не забывать проверять, является ли что-то нулевым, прежде чем пытаться прочитать или изменить то, на что оно ссылается.
Почти каждый популярный сегодня язык имеет этот недостаток. Первый ученый-компьютерщик
Тони Хоар ввел нулевые ссылки в язык ALGOL еще в 19 году.65, а позже он был включен во многие другие языки. Хор объяснил, что сделал это «просто потому, что это было так легко реализовать», но сегодня он считает это «ошибкой на миллиард долларов». Это потому, что это вызвало бесчисленное количество ошибок, когда ссылка, которую программист считает действительной, на самом деле является нулевой ссылкой.
Разработчики программного обеспечения должны быть предельно дисциплинированы, чтобы избежать таких ловушек, и иногда они не принимают адекватных мер предосторожности. Архитекторы структурного программирования знали, что это справедливо для операторов GOTO, и не оставили разработчикам лазейки. Чтобы гарантировать улучшения ясности, которые обещал код без GOTO, они знали, что им придется полностью исключить его из своих языков структурированного программирования.
История доказывает, что удаление опасной функции может значительно улучшить качество кода. Сегодня у нас есть множество опасных практик, которые ставят под угрозу надежность и ремонтопригодность программного обеспечения. Почти все современные языки программирования имеют ту или иную форму нулевых ссылок, общее глобальное состояние и функции с побочными эффектами — вещи, которые намного хуже, чем когда-либо был GOTO.
Как можно устранить эти недостатки? Оказывается, ответ
существует уже несколько десятилетий: чисто функциональные языки программирования.
Из дюжины языков функционального программирования Haskell, безусловно, является самым популярным, судя по количеству репозиториев GitHub, использующих эти языки.
Первый чисто функциональный язык, ставший популярным, называется
Haskell был создан в 1990 году. Таким образом, к середине 1990-х мир разработки программного обеспечения действительно имел решение досадных проблем, с которыми он все еще сталкивается. К сожалению, аппаратное обеспечение того времени часто было недостаточно мощным, чтобы использовать это решение. Но современные процессоры легко справляются с требованиями Haskell и других чисто функциональных языков.
Действительно, программное обеспечение, основанное на чистых функциях, особенно хорошо подходит для современных
многоядерные процессоры. Это связано с тем, что чистые функции работают только со своими входными параметрами, что делает невозможным какое-либо взаимодействие между различными функциями. Это позволяет оптимизировать компилятор для создания кода, который эффективно и легко работает на нескольких ядрах.
Как следует из названия, при чисто функциональном программировании разработчик может писать только чистые функции, которые по определению не могут иметь побочных эффектов. С помощью этого единственного ограничения вы повышаете стабильность, открываете дверь для оптимизации компилятора и в конечном итоге получаете код, который намного легче анализировать.
Но что, если функция должна знать или управлять состоянием системы? В этом случае состояние передается через длинную цепочку так называемых составных функций — функций, которые передают свои выходные данные на входы следующей функции в цепочке. При передаче состояния от функции к функции каждая функция имеет к нему доступ, и нет никаких шансов, что другой параллельный программный поток изменит это состояние — еще одна распространенная и дорогостоящая уязвимость, встречающаяся в слишком многих программах.
В функциональном программировании также есть решение «ошибки на миллиард долларов» Хоара — нулевых ссылок. Он решает эту проблему, запрещая нули. Вместо этого существует конструкция, обычно называемая
Он решает эту проблему, запрещая нули. Вместо этого существует конструкция, обычно называемая
Может быть (или Опция на некоторых языках). A Может быть может быть Ничего или Просто некоторое значение. Работа с Возможно s заставляет разработчиков всегда учитывать оба случая. У них нет выбора в этом вопросе. Они должны справиться с Ничего случай каждый раз, когда они сталкиваются с Возможно . Это устраняет множество ошибок, которые могут порождать нулевые ссылки.
Функциональное программирование также требует, чтобы данные были неизменяемыми, а это означает, что если вы присвоите переменной какое-то значение, это значение останется навсегда. Переменные больше похожи на переменные в математике. Например, чтобы вычислить формулу,
y = x 2 + 2 x – 11, вы выбираете значение для x и ни разу во время вычисления y означает, что x принимают другое значение. Таким образом, при вычислении x 2 используется то же значение для x , что и при вычислении 2 x . В большинстве языков программирования такого ограничения нет. Вы можете вычислить x 2 с одним значением, затем изменить значение x перед вычислением 2 x . Запрещая разработчикам изменять (мутировать) значения, они могут использовать те же рассуждения, что и на уроках алгебры в средней школе.
Таким образом, при вычислении x 2 используется то же значение для x , что и при вычислении 2 x . В большинстве языков программирования такого ограничения нет. Вы можете вычислить x 2 с одним значением, затем изменить значение x перед вычислением 2 x . Запрещая разработчикам изменять (мутировать) значения, они могут использовать те же рассуждения, что и на уроках алгебры в средней школе.
В отличие от большинства языков, языки функционального программирования глубоко укоренены в математике. Именно это происхождение в высокодисциплинированной области математики дает функциональным языкам их самые большие преимущества.
Почему это? Это потому, что люди работали над математикой в течение тысяч лет. Это довольно солидно. Большинство парадигм программирования, таких как объектно-ориентированное программирование, имеют за плечами не более полдюжины десятков лет работы. По сравнению с ними они грубы и незрелы.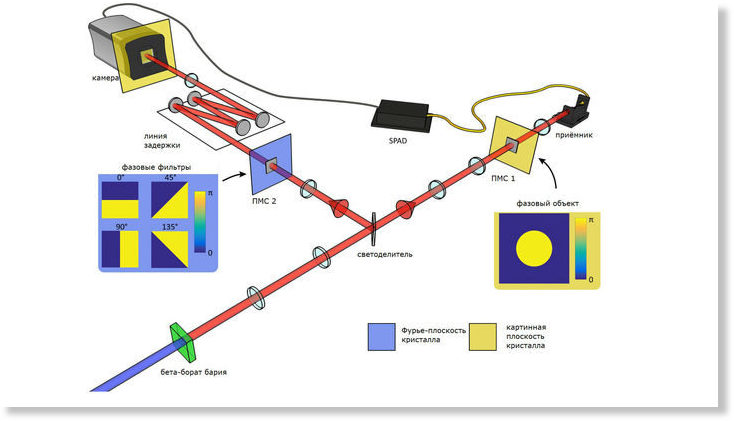
Представьте, что каждый раз, когда вы включаете микроволновую печь, настройки вашей посудомоечной машины менялись с обычного цикла на кастрюли и сковородки. В программном обеспечении такие вещи происходят постоянно.
Позвольте мне привести пример того, насколько программирование небрежно по сравнению с математикой. Обычно мы учим новых программистов забывать то, что они узнали на уроках математики, когда они впервые сталкиваются с оператором
х = х + 1 . В математике это уравнение не имеет решений. Но в большинстве современных языков программирования х = х + 1 не является уравнением. Это оператор , который дает компьютеру команду взять значение x , добавить к нему единицу и поместить обратно в переменную с именем x .
В функциональном программировании нет операторов, только
выражений . Математическое мышление, которому мы научились в средней школе, теперь можно использовать при написании кода на функциональном языке.
Благодаря функциональной чистоте вы можете рассуждать о коде, используя алгебраическую замену, чтобы уменьшить сложность кода так же, как вы уменьшали сложность уравнений на уроках алгебры. В нефункциональных языках (императивных языках) нет эквивалентного механизма для рассуждений о том, как работает код.
Функциональное программирование имеет крутую кривую обучения
Чисто функциональное программирование решает многие из самых больших проблем нашей отрасли, удаляя опасные функции из языка, что затрудняет для разработчиков возможность выстрелить себе в ногу. Поначалу эти ограничения могут показаться радикальными, так как я уверен, что разработчики 1960-х отнеслись к удалению GOTO. Но в том-то и дело, что работа на этих языках одновременно и освобождает, и расширяет возможности — настолько, что почти все самые популярные сегодня языки включают в себя функциональные возможности, хотя по своей сути они остаются императивными языками.
Самая большая проблема с этим гибридным подходом заключается в том, что он по-прежнему позволяет разработчикам игнорировать функциональные аспекты языка. Если бы мы оставили GOTO в качестве опции 50 лет назад, мы могли бы до сих пор бороться со спагетти-кодом.
Если бы мы оставили GOTO в качестве опции 50 лет назад, мы могли бы до сих пор бороться со спагетти-кодом.
Чтобы воспользоваться всеми преимуществами чисто функциональных языков программирования, вы не можете идти на компромисс. Вам нужно использовать языки, которые были разработаны с учетом этих принципов с самого начала. Только приняв их, вы получите множество преимуществ, которые я описал здесь.
Но функциональное программирование — это не ложе из роз. Это дорого обходится. Научиться программировать в соответствии с этой функциональной парадигмой — это почти то же самое, что заново научиться программировать с самого начала. Во многих случаях разработчики должны ознакомиться с математикой, которую они не изучали в школе. Требуемая математика не сложна — она просто нова и для тех, кто боится математики, страшна.
Что еще более важно, разработчики должны научиться новому мышлению. Сначала это будет в тягость, потому что они к этому не привыкли. Но со временем этот новый способ мышления становится второй натурой и в конечном итоге снижает когнитивные издержки по сравнению со старыми способами мышления. Результатом является значительный прирост эффективности.
Результатом является значительный прирост эффективности.
Но переход к функциональному программированию может быть трудным. Мое собственное путешествие, проделавшее это несколько лет назад, является показательным.
Я решил выучить Haskell — и мне нужно было сделать это в рамках бизнес-плана. Это был самый трудный опыт обучения за всю мою 40-летнюю карьеру, в значительной степени потому, что не было окончательного источника помощи разработчикам в переходе к функциональному программированию. Действительно, за предыдущие три десятилетия никто не написал ничего всеобъемлющего о функциональном программировании.
Чтобы воспользоваться всеми преимуществами чисто функциональных языков программирования, вы не можете идти на компромисс. Вам нужно использовать языки, которые были разработаны с учетом этих принципов с самого начала.
Мне оставалось собирать по кусочкам то здесь, то там и повсюду. И я могу засвидетельствовать грубую неэффективность этого процесса. Мне потребовалось три месяца дней, ночей и выходных, чтобы жить и дышать Хаскеллом. Но, в конце концов, я дошел до того, что с его помощью я мог писать код лучше, чем с чем-либо еще.
Мне потребовалось три месяца дней, ночей и выходных, чтобы жить и дышать Хаскеллом. Но, в конце концов, я дошел до того, что с его помощью я мог писать код лучше, чем с чем-либо еще.
Когда я решил, что наша компания должна перейти на использование функциональных языков, я не хотел подвергать своих разработчиков такому же кошмару. Итак, я начал создавать для них учебную программу, которая стала основой для книги, призванной помочь разработчикам стать функциональными программистами. В
В своей книге я даю руководство по овладению функциональным языком под названием PureScript, который украл все замечательные аспекты Haskell и улучшил многие из его недостатков. Кроме того, он может работать как в браузере, так и на внутреннем сервере, что делает его отличным решением для многих современных требований к программному обеспечению.
Хотя такие учебные ресурсы могут только помочь, для того, чтобы этот переход произошел в широких масштабах, компании, работающие с программным обеспечением, должны больше инвестировать в свой самый большой актив: в своих разработчиков. В моей компании,
В моей компании,
Panoramic Software, где я являюсь техническим директором, мы сделали эти инвестиции, и вся новая работа выполняется либо на PureScript, либо на Haskell.
Мы начали переходить на функциональные языки три года назад, начав с еще одного чисто функционального языка под названием
Elm, потому что это более простой язык. (Мы и не подозревали, что в конце концов перерастем его.) Нам потребовалось около года, чтобы начать пожинать плоды. Но с тех пор, как мы преодолели горб, это было замечательно. У нас не было ошибок рабочего времени выполнения, которые были так распространены в том, что мы раньше использовали, JavaScript на передней части и Java на задней. Это улучшение позволило команде потратить гораздо больше времени на добавление новых функций в систему. Теперь мы почти не тратим время на отладку производственных проблем.
Но при работе с языком, который используется относительно немногими другими, по-прежнему возникают проблемы, в частности, отсутствие интерактивной справки, документации и примеров кода. И сложно нанять разработчиков с опытом работы на этих языках. Поэтому моя компания пользуется услугами рекрутеров, которые специализируются на поиске функциональных программистов. И когда мы нанимаем кого-то без опыта функционального программирования, мы проводим с ним обучение в течение первых нескольких месяцев, чтобы ввести его в курс дела.
И сложно нанять разработчиков с опытом работы на этих языках. Поэтому моя компания пользуется услугами рекрутеров, которые специализируются на поиске функциональных программистов. И когда мы нанимаем кого-то без опыта функционального программирования, мы проводим с ним обучение в течение первых нескольких месяцев, чтобы ввести его в курс дела.
Будущее функционального программирования
Моя компания небольшая. Он поставляет программное обеспечение правительственным учреждениям, чтобы они могли помочь ветеранам получать льготы от
Департамент по делам ветеранов США. Это чрезвычайно полезная работа, но это не прибыльная сфера. При минимальной марже мы должны использовать все доступные нам инструменты, чтобы делать больше с меньшим количеством разработчиков. И для этого функциональное программирование — как раз то, что нужно.
Непривлекательные компании вроде нашей очень часто испытывают трудности с привлечением разработчиков. Но теперь мы можем нанимать высококлассных специалистов, потому что они хотят работать над функциональной кодовой базой. Опережая эту тенденцию, мы можем получить таланты, о которых большинство компаний нашего размера могли только мечтать.
Опережая эту тенденцию, мы можем получить таланты, о которых большинство компаний нашего размера могли только мечтать.
Я ожидаю, что внедрение чисто функциональных языков улучшит качество и надежность всей индустрии программного обеспечения, а также значительно сократит время, затрачиваемое на устранение ошибок, которые просто невозможно сгенерировать с помощью функционального программирования. Это не волшебство, но иногда мне так кажется, и каждый раз, когда мне приходится работать с нефункциональной кодовой базой, я вспоминаю, как хорошо у меня это получается.
Одним из признаков того, что индустрия программного обеспечения готовится к смене парадигмы, является то, что функциональные возможности появляются во все большем количестве популярных языков. Отрасли потребуется гораздо больше работы, чтобы полностью осуществить переход, но преимущества этого очевидны, и, без сомнения, дело движется именно к этому.
Источники запутанных фотонных пар | NIST
Главная Публикации Ссылки Сотрудничество Командные разработки Возможности
Разработка источников пар запутанных фотонов:
Пары запутанных фотонов важны для реализации квантовой связи и квантовых вычислений. Наша основная цель — разработать пары фотонов, которые могут взаимодействовать между летающими фотонными кубитами в оптическом волокне и стационарными атомными кубитами в квантовой памяти. В качестве первого шага мы экспериментально реализовали невырожденный последовательный источник запутанных фотонных пар с временным интервалом [1]. На втором этапе наши усилия сосредоточены на сужении ширины спектральной линии пар фотонов, чтобы они могли эффективно взаимодействовать с атомами в квантовой памяти [2].
Наша основная цель — разработать пары фотонов, которые могут взаимодействовать между летающими фотонными кубитами в оптическом волокне и стационарными атомными кубитами в квантовой памяти. В качестве первого шага мы экспериментально реализовали невырожденный последовательный источник запутанных фотонных пар с временным интервалом [1]. На втором этапе наши усилия сосредоточены на сужении ширины спектральной линии пар фотонов, чтобы они могли эффективно взаимодействовать с атомами в квантовой памяти [2].
| Экспериментальная установка, показывающая кристаллический волновод, в котором генерируются пары фотонов. |
Невырожденный последовательный источник запутанных фотонных пар с временным интервалом генерируется из периодически поляризованного калий-титанилфосфатного волновода путем параметрического преобразования частоты с понижением частоты (FPDC) на тактовой частоте 1 ГГц. Длины волн сигнала и холостого хода составляют 895 нм и 1310 нм. Фотоны с длиной волны 1310 нм подходят для оптической связи на большие расстояния, а фотоны с длиной волны 895 нм соответствуют первой линии перехода атомов Cs, что подходит для исследования квантовой памяти. Для регистрации фотонов на длине волны 895 нм используется кремниевый лавинный фотодиод, а для регистрации фотонов на длине волны 1310 нм используется разработанный в нашей лаборатории ап-конверсионный детектор на основе периодически поляризованного волновода на основе ниобата лития [3]. Измеренная скорость потока пар запутанных фотонов составляет 650 Гц, а видимость интерференционных полос составляет 79,4% без вычитания шума.
Длины волн сигнала и холостого хода составляют 895 нм и 1310 нм. Фотоны с длиной волны 1310 нм подходят для оптической связи на большие расстояния, а фотоны с длиной волны 895 нм соответствуют первой линии перехода атомов Cs, что подходит для исследования квантовой памяти. Для регистрации фотонов на длине волны 895 нм используется кремниевый лавинный фотодиод, а для регистрации фотонов на длине волны 1310 нм используется разработанный в нашей лаборатории ап-конверсионный детектор на основе периодически поляризованного волновода на основе ниобата лития [3]. Измеренная скорость потока пар запутанных фотонов составляет 650 Гц, а видимость интерференционных полос составляет 79,4% без вычитания шума.
| Кривая запутанных пар фотонов |
структуру со средним π-фазосдвигателем на нелинейно-оптический кристаллический волновод. В сотрудничестве с университетом Мэриленда в округе Балтимор мы теоретически изучили ширину линий сигнальных и холостых фотонов в процессе SPDC. Исходя из наших теоретических расчетов, подход обещает генерировать сигнал очень узкой ширины линии (от ~ ГГц до суб-ГГц) и холостые фотоны через SPDC.
Исходя из наших теоретических расчетов, подход обещает генерировать сигнал очень узкой ширины линии (от ~ ГГц до суб-ГГц) и холостые фотоны через SPDC.
| Narrowed linewidth with Bragg grating on waveguide |
[1] Lijun Ma, Oliver Slattery, Tiejun Chang and Xiao Tang, «Non-degenerated sequential time-bin генерация запутывания с использованием периодически поляризованного волновода КТП».
Подробнее см.: Optics Express, Vol. 17 Выпуск 18, стр. 15799-15807 (2009). PDF: http://www.opticsinfobase.org/abstract.cfm?id=185209&CFID=106038750&CFTOKEN=10685436
[2] Ли Ян, Лицзюнь Ма и Сяо Тан, «Узкополосное параметрическое преобразование с понижением частоты, усиленное брэгговской решеткой», OPTICS EXPRESS, Vol. 18, № 6, 5957 (март 2010 г.). http://www.opticsinfobase.org/abstract.cfm?URI=oe-18-6-5957
[3] Лицзюнь Ма, Оливер Слэттери и Сяо Тан, «Экспериментальное исследование высокочувствительного инфракрасного спектрометра с -конверсионный детектор», Optics Express Vol.