Квантовые вычисления против классических: зачем нам столько цифр. Квантовые вычисления
зачем нам столько цифр / Блог компании Сбербанк / Хабр
Классические вычисления: AND, OR, NOT
Чтобы разобраться с квантовыми вычислениями, стоит для начала освежить знания о классических. Здесь единицей обрабатываемой информации является бит. Каждый бит может находиться только в одном из двух возможных состояний – 0 или 1. Регистр из N бит может содержать одну из 2N возможных комбинаций состояний и представляется в виде их последовательности.Для обработки и преобразования информации используются побитовые операции, пришедшие из булевой алгебры. Основные операции — это однобитная NOT и двубитные AND и OR. Битовые операции описываются через таблицы истинности. В них приводится соответствие входных аргументов получаемому значению.
Алгоритм классических вычислений — это набор последовательных битовых операций. Удобней всего воспроизводить его графически, в виде схемы из функциональных элементов (СФЭ), где каждая операция имеет свое обозначение. Вот пример СФЭ для проверки двух бит на эквивалентность.
Квантовые вычисления. Физическая основа
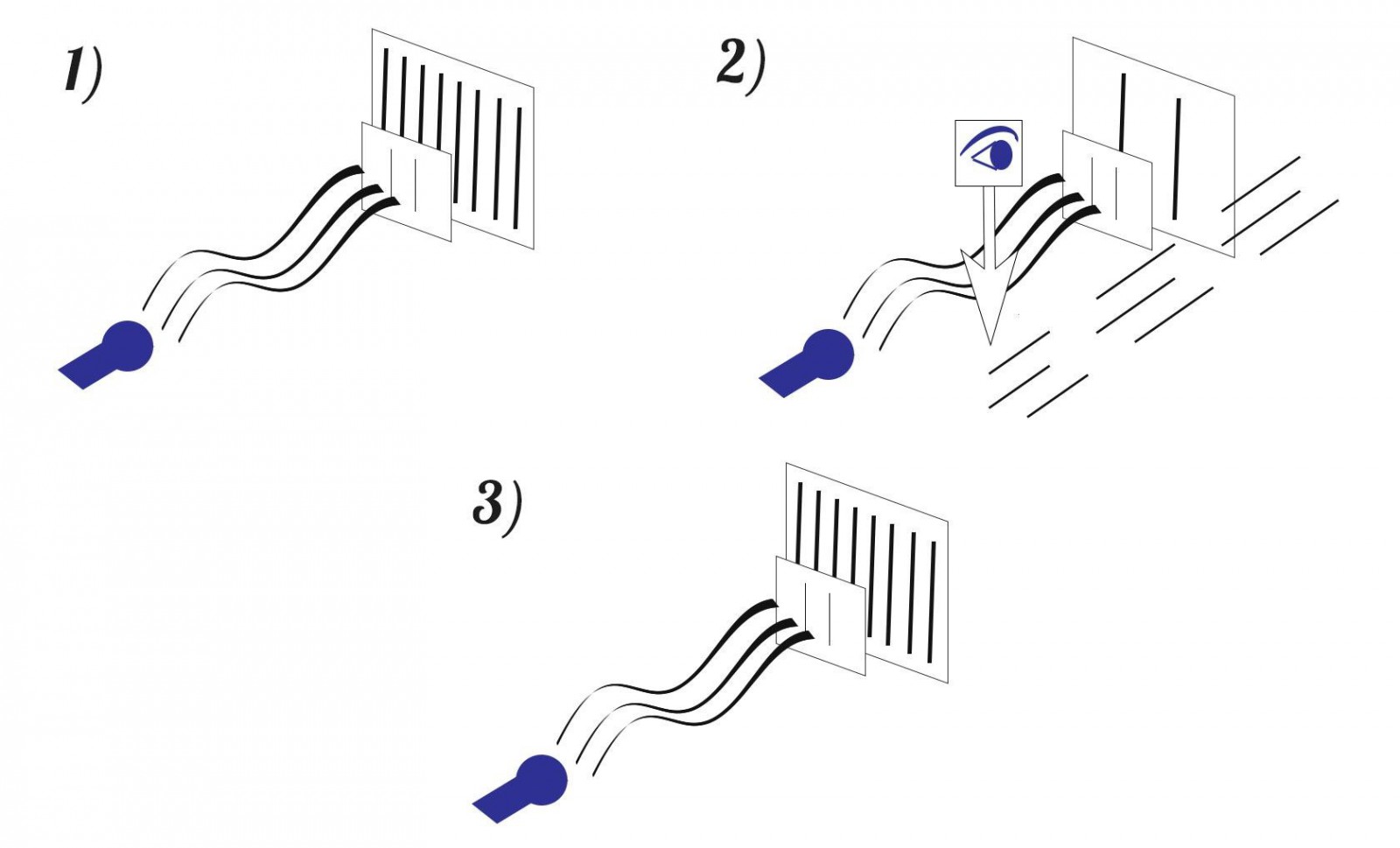
А теперь перейдем к новой теме. Квантовые вычисления — это альтернатива классическим алгоритмам, основанная на процессах квантовой физики. Она гласит, что без взаимодействия с другими частицами (то есть до момента измерения), электрон не имеет однозначных координат на орбите атома, а одновременно находится во всех точках орбиты. Область, в которой находится электрон, называется электронным облаком. В ходе известного эксперимента с двумя щелями один электрон проходит одновременно через обе щели, интерферируя при этом с самим собой. Только при измерении эта неопределенность схлопывается и координаты электрона становятся однозначными.Кубиты
В квантовых вычислениях физические свойства квантовых объектов реализованы в так называемых кубитах (q-bit). Классический бит может находиться только в одном состоянии – 0 или 1. Кубит до измерения может находиться одновременно в обоих состояниях, поэтому его принято обозначать выражением a|0⟩ + b|1⟩, где A и B — комплексные числа, удовлетворяющие условию |A|2+|B|2=1. Измерение кубита мгновенно «схлопывает» его состояние в одно из базисных – 0 или 1. При этом «облако» коллапсирует в точку, первоначальное состояние разрушается, и вся информация о нем безвозвратно теряется.Одно из применений этого свойства – кот Шредингера генератор истинно случайных чисел. Кубит вводится в такое состояние, при котором результатом измерения могут быть 1 или 0 с одинаковой вероятностью. Это состояние описывается так:
Квантовые и классические вычисления. Первый раунд
Начнем с основ. Имеется набор исходных данных для вычислений, представленный в двоичном формате векторами длиной N.В памяти квантового компьютера одновременно представлены все 2n комбинации исходных данных. Преобразования применяются ко всем этим комбинациям сразу. В результате за одну операцию мы вычисляем функцию для всех 2n возможных вариантов набора данных (измерение в итоге все равно даст только одно решение, но об этом позже).
И в классических, и в квантовых вычислениях используются логические преобразования — гейты. В классических вычислениях входные и выходные значения хранятся в разных битах, а значит в гейтах количество входов может отличаться от количества выходов:
Рассмотрим реальную задачу. Нужно определить, эквивалентны ли два бита.
Если при классических вычислениях на выходе получаем единицу, значит эквивалентны, иначе нет:
Теперь представим эту задачу с помощью квантовых вычислений. В них все гейты преобразований имеют столько же выходов, сколько входов. Это связано с тем, что результатом преобразования является не новое значение, а изменение состояния текущих.
В примере мы сравниваем значения первого и второго кубитов. Результат будет в нулевом кубите — кубите-флаге. Данный алгоритм применим только к базовым состояниям – 0 или 1. Вот порядок квантовых преобразований.
- Воздействуем на кубит-флаг гейтом «Не», выставляя его в 1.
- Два раза применяем двухкубитный гейт «Контролируемое Не». Этот гейт меняет значение кубита-флага на противоположное только в случае, если второй кубит, участвующий в преобразовании, находится в состоянии 1.
- Измеряем нулевой кубит. Если в результате получили 1, значит и первый, и второй кубиты либо оба в состоянии 1 (кубит-флаг два раза поменял свое значение), либо в состоянии 0 (кубит-флаг так и остался в состоянии 1). Иначе кубиты находятся в разных состояниях.
Следующий уровень. Квантовые однокубитные гейты Паули
Попробуем сравнить классические и квантовые вычисления в более серьезных задачах. Для этого нам потребуется еще немного теоретических знаний.В квантовых вычислениях обрабатываемая информация закодирована в квантовых битах – так называемых кубитах. В простейшем случае кубит, как и классический бит, может находиться в одном из двух базисных состояний: |0⟩ (краткое обозначение для вектора 1|0⟩ + 0|1⟩) и |1⟩ (для вектора 0|0⟩ + 1|1⟩). Квантовый регистр представляет собой тензорное произведение векторов кубит. В простейшем случае, когда каждый кубит находится в одном из базисных состояний, квантовый регистр эквивалентен классическому. Регистр из двух кубит, находящихся в состоянии |0>, можно расписать в таком виде:
(1|0⟩ + 0|1⟩)*(1|0⟩ + 0|1⟩) = 1|00⟩ + 0|01⟩ + 0|10⟩ + 0|11⟩ = |00⟩.
Для обработки и преобразования информации в квантовых алгоритмах используются так называемые квантовые вентили (гейты). Они представляются в виде матрицы. Для получения результата применения гейта, нам необходимо умножить вектор, характеризующий кубит, на матрицу гейта. Первая координата вектора – множитель перед |0⟩, вторая координата – множитель перед |1⟩. Матрицы основных однокубитных гейтов выглядит так:
А вот пример применения гейта Not:
X * |0⟩ = X * (1|0⟩ + 0|1⟩) = 0|0⟩ + 1|1⟩ = |1⟩
Множители перед базисными состояниями называются амплитудами и являются комплексными числами. Модуль комплексного числа равен корню из суммы квадратов действительной и мнимой частей. Квадрат модуля амплитуды, стоящей перед базисным состоянием, равен вероятности получить это базисное состояние при измерении кубита, поэтому сумма квадратов модулей амплитуд всегда равна 1. Мы могли бы использовать произвольные матрицы для преобразований над кубитами, но из-за того, что норма (длина) вектора всегда должна быть равна 1 (сумма вероятностей всех исходов всегда равна 1), наше преобразование должно сохранять норму вектора. Значит преобразование должно быть унитарным и соответствующая ему матрица унитарной. Напомним, что унитарное преобразование обратимо и UU†=I.
Для более наглядной работы с кубитами их изображают векторами на сфере Блоха. В такой интерпретации однокубитные гейты представляют собой вращение вектора кубита вокруг одной из осей. Например гейт Not (X) поворачивает вектор кубита на Pi относительно оси X. Таким образом, состояние |0>, представляемое вектором, направленным строго вверх, переходит в состояние |1>, направленное строго вниз. Состояние кубита на сфере Блоха определяется формулой cos(θ/2)|0⟩+eiϕsin(θ/2)|1⟩
Квантовые двухкубитные гейты
Для построения алгоритмов нам недостаточно только однокубитных гейтов. Необходимы гейты, которые осуществляют преобразования в зависимости от некоторых условий. Основным таким инструментом является двухкубитный гейт CNOT. Этот гейт применяется к двум кубитам и инвертирует второй кубит только в том случае, если первый кубит находится в состоянии |1⟩. Матрица гейта CNOT выглядит так:А вот пример применения:
CNOT *|10⟩ = CNOT * (0|00⟩ + 0|01⟩ + 1|10⟩ + 0|11⟩) = 0|00⟩ + 0|01⟩ + 1|11⟩ + 0|10⟩ = |11⟩
Применение гейта CNOT эквивалентно выполнению классической операции XOR с записью результата во второй кубит. Действительно, если посмотреть на таблицу истинности оператора XOR и CNOT, то увидим соответствие:
| XOR | CNOT | |||
| 0 | 0 | 0 | 00 | 00 |
| 0 | 1 | 1 | 01 | 01 |
| 1 | 0 | 1 | 10 | 11 |
| 1 | 1 | 0 | 11 | |
У гейта CNOT есть интересное свойство – после его применения кубиты запутываются или распутываются, в зависимости от исходного состояния. Это будет показано в следующей статье, в разделе про квантовый параллелизм.
Построение алгоритма — классическая и квантовая реализация
Имея полный арсенал квантовых гейтов, мы можем приступать к разработке квантовых алгоритмов. В графическом представлении кубиты представляются прямыми линиями – «струнами», на которые накладываются гейты. Однокубитные гейты Паули обозначаются обычными квадратами, внутри которых изображается ось вращения. Гейт CNOT выглядит немного сложнее:Пример применения гейта CNOT:
Одним из важнейших действий в алгоритме является измерение полученного результата. Измерение обычно обозначается дуговой шкалой со стрелкой и обозначением, относительно какой оси идет измерение.
Итак, попробуем построить классический и квантовый алгоритм, который прибавляет 3 к аргументу.
Суммирование обычных чисел столбиком подразумевает совершение двух действий над каждым разрядом – сумму самих цифр разряда и сумму результата с переносом с предыдущей операции, если таковой перенос был.
В двоичном представлении чисел операция суммирования будет состоять из тех же действий. Приведем код на языке python:
arg = [1,1] #задаем аргумент result = [0,0,0] #инициализируем результат carry1 = arg[1] & 0x1 #складываем с 0b11, так что перенос от младшего бита появится в том случае, если у агрумента младший бит = 1 result[2] = arg[1] ^ 0x1 #складываем младшие биты carry2 = carry1 | arg[0] #складываем с 0b11, так что перенос от старшего бита появится в том случае, если у агрумента старший бит = 1 или был перенос с младшего бита result[1] = arg[0] ^ 0x1 #складываем старшие биты result[1] ^= carry1 #применяем перенос с младшего бита result[0] ^= carry2 #применяем перенос со старшего бита print(result) Теперь попробуем разработать аналогичную программу для квантового вычислителя:В этой схеме первые два кубита – это аргумент, следующие два – переносы, оставшиеся 3 – результат. Вот как работает алгоритм.
- Первым шагом до барьера мы выставляем аргумент в то же состояние, как и в классическом случае – 0b11.
- С помощью оператора CNOT вычисляем значение первого переноса – результат операции arg & 1 равен единице только тогда, когда arg равен 1, в этом случае мы инвертируем второй кубит.
- Следующие 2 гейта реализуют сложение младших бит – мы переводим кубит 4 в состояние |1⟩ и результат XOR записываем в него же.
- Большим прямоугольником обозначен гейт CCNOT – расширение гейта CNOT. В этом гейте два управляющих кубита и третий инвертируется только в том случае, если первые два находятся в состоянии |1. Комбинация из 2 гейт CNOT и одного CCNOT дает нам результат классической операции carry2 = carry1 | arg[0]. Первые 2 гейта выставляют перенос в единицу в том случае, если один из них равен 1, а гейт CCNOT обрабатывает случай, когда они оба равны единице.
- Складываем старшие кубиты и кубиты переноса.
Промежуточные выводы
Запустив оба примера, мы получим один и тот же результат. На квантовом компьютере это займет больше времени, потому что необходимо провести дополнительную компиляцию в квантовоассемблерный код и отправить его на исполнение в облако. Использование квантовых вычислений имело бы смысл, если бы скорость выполнения их элементарных операций – гейтов – была бы во много раз меньше чем в классической модели.Измерения специалистов показывают, что выполнение одного гейта занимает около 1 наносекунды. Так что алгоритмы для квантового вычислителя должны не копировать классические, а по максимуму использовать уникальные свойства квантовой механики. В следующей статье мы разберем одно из основных таких свойств — квантовый параллелизм — и поговорим о квантовой оптимизации в целом. Затем определим наиболее подходящие сферы для квантовых вычислений и расскажем об их применении.
По материалам Дмитрия Сапаева, старшего руководителя направления по развитию ИТ-систем в отделе разработки ЦТИ Сбербанк-Технологий, и Дмитрия Булычкова, директора проектов в Центре технологических инноваций Сбербанка.
UPD: Мы опубликовали вторую часть статьи, где погружаемся в квантовые вычисления более глубоко и рассказываем об их практическом применении.
habr.com
отжиг с выключателями и прочее веселье / Блог компании Сбербанк / Хабр
Квантовый параллелизм
Согласно законам квантовой механики, частица может находиться во всех своих состояниях одновременно. Это состояние кубита называется суперпозиция. В суперпозиции амплитуды базисных состояний принимают ненулевые значения – a|0⟩ + b|1⟩ и при этом сохраняется требование нормировки.Квантовая частица может находиться в суперпозиции только до момента измерения. После измерения она коллапсирует в одно из своих базисных состояний – 0 или 1. Если мы имеем регистр кубитов, которые находятся в суперпозиции, то состояние самого регистра можно определить следующим образом:
(a0|0⟩ + b0|1⟩)(a1|0⟩ + b1|1⟩)…(an|0⟩ + bn|1⟩) = a0×a1×…×an|00..0⟩ + a0×a1×…×bn|00…1⟩ +…+ b0×b1×…×bn|11…1⟩
Важно понимать, что множители, которые стоят перед состояниями, – это не вероятность. Иначе мы бы получили классическую систему с ограничением – неизвестно, в каком именно состоянии она находится. А квантовый бит находится в обоих состояниях одновременно. Мы имеем возможность обработки сразу всех 2n возможных комбинаций!
Для того чтобы перевести кубит в состояние суперпозиции, нужно применить к нему специальное преобразование – гейт Адамара. Еще одно применение гейта Адамара вернет кубит в одно из базисных состояний. Так выглядит матрица гейта Адамара и пример его применения:
H×|0⟩ = H×(1|0⟩ + 0|1⟩) = 1/sqr(2)|0⟩ + 1/sqr(2)|1⟩ H×(1/sqr(2)|0⟩ + 1/sqr(2)|1⟩) = 1|0⟩ + 0|1⟩ = |0⟩
Интересно действие двухкубитного гейта CNOT при контролирующем кубите в суперпозиции – CNOT запутывает кубиты. Запутанное состояние – это явление, при котором кубиты нельзя рассматривать по отдельности, так как их состояние теперь общее.
Приведем пример. Допустим, у нас есть регистр из двух кубитов в начальном состоянии — в базисном состоянии |0⟩). Применим гейт Адамара к первому кубиту – получим следующее состояние регистра:
H×I×|00⟩= H×(1|0⟩ + 0|1⟩) × I×(1|0⟩ + 0|1⟩) = (1/sqr(2)|0⟩ + 1/sqr(2)|1⟩) × (1|0⟩ + 0|1⟩) = 1/sqr(2)|00⟩ + 1/sqr(2)|10⟩
Первый и второй кубиты в этом регистре независимы друг от друга. Второй кубит до сих пор в состоянии |0⟩ и если мы его измерим, то все равно не получим информации о состоянии первого – тот может быть как в состоянии 0, так и в состоянии 1. Применим двухкубитный гейт CNOT:
CNot × (1/sqr(2)|00⟩ + 1/sqr(2)|10⟩) = CNot × (1/sqr(2)|00⟩ + 0|01⟩ + 1/sqr(2)|10⟩ + 0|11⟩) = 1/sqr(2)|00⟩ + 0|01⟩ + 0|10⟩ + 1/sqr(2)|11⟩ = 1/sqr(2)|00⟩ + 1/sqr(2)|11⟩
Теперь кубиты находятся в запутанном состоянии, и измерение любого из них заставит немедленно коллапсировать другой! Состояние регистра показывает, что оба кубита находятся в одинаковом состоянии — 0 или 1. Так что измерив один, мы точно узнаем состояние другого.
После того, как мы запутали кубиты, нельзя просто так свернуть один из них в базисное состояние – их нужно сначала распутать. Попробуйте самостоятельно создать данную схему на квантовом редакторе IBM и оцените результат:
Коллапс и количество получаемой информации
Производя вычисления над квантовым регистром из n кубитов, мы имеем возможность одновременно обрабатывать все 2n возможных состояния. Однако при измерении каждый кубит коллапсирует в одно из своих базисных состояний, а значит — после измерения результата у нас нет возможности получить больше информации, чем в классическом случае – мы получим только одно из возможных состояний с соответствующей вероятностью.Квантовые алгоритмы учитывают это свойство и предлагают множество подходов для решения конкретного класса задач. Например, в одном из подходов проводится множество такого типа преобразований, которые увеличивают амплитуду искомого решения и уменьшают амплитуды остальных.
Алгоритм Гровера
Алгоритм, представляющий множество таких преобразований, называется алгоритмом Гровера. Он позволяет квадратично ускорить поиск в неструктурированной БД. Обычно сложность поиска в неструктурированном наборе данных равна O(n), то есть в худшем случае нам необходимо просмотреть все записи. Квантовый алгоритм позволяет решить эту задачу за O(√n).Например, у нас есть 40 бит и нам нужно найти одну из всех возможных комбинаций, удовлетворяющую некоторому условию. В классическом случае нам понадобится обработать порядка 1 000 000 000 000 разных комбинаций. Квантовый алгоритм позволит получить результат за 1 000 000.
Рассмотрим пример. У нас имеется регистр из n кубитов, находящихся в суперпозиции. Таким образом, у нас есть 2n всех возможных состояний, и амплитуда каждого равна 1/√2n (именно при таком значении сумма квадратов модулей будет равна 1). Изобразим это в виде диаграммы:
Также у нас есть один дополнительный кубит, который мы будем называть функциональным, и функция-оракул. Оракул переводит функциональный кубит из базисного состояния |0⟩ в состояние |1⟩ ровно на том наборе, который мы ищем.Чтобы при измерении получить именно то состояние, которое соответствует функции-оракулу, мы проделываем следующие действия:
- Изменяем знак амплитуды искомого значения на отрицательный. Для этого переводим функциональный кубит в состояние |1⟩ на всех наборах, далее применяем к нему гейт Адамара и затем функцию-оракул ко всему регистру. После этого действия картина будет выглядеть так:
- Так как мы обрабатываем все состояния одинаково, то не можем изменить какую-то одну амплитуду. Но можем сделать инверсию относительно среднего – отобразить значение амплитуды, взяв за ось значение среднего:
- Как мы видим, значение искомой амплитуды выросло относительно остальных. По итогам выполнения этого набор действий порядка Pi×0,25×√2n раз, искомая амплитуда будет почти равна единице.
Квантовая оптимизация
Все рассмотренные ранее алгоритмы и приемы справедливы для так называемого универсального квантового компьютера – вычислителя, способного производить элементарные преобразования и фактически решать любую задачу (в простейшем случае моделируя классический алгоритм).Но существует целый пласт математических задач, в которых как таковые вычисления не требуются, а необходимо найти такую комбинацию аргументов, на которой определённого вида функция примет минимальное значение. Этот класс задач – задачи оптимизации — подробнее будет разобран далее.
Квантовый отжиг
Отжиг — процесс постепенного остывания вещества, при котором молекулы на фоне замедления теплового движения собираются в наиболее энергетически выгодные конфигурации. Термин «отжиг» пришёл из металлургии. В более энергетически выгодном состоянии металл становится одновременно твёрже и прочней: требуется большее внешнее воздействие, большая механическая работа над куском металла, чтобы нарушить выгодную конфигурацию молекул, «приподнять» эту конфигурацию над самым дном энергетической ямы.Подобно классическому отжигу, при медленном включении межчастичного взаимодействия квантовая система «ищет» энергетически наиболее выгодную конфигурацию посредством эффектов квантовой механики. Квантовые вычисления на основе квантового отжига позволяют решать определенные проблемы, которые затруднительно решать с использованием классических компьютеров.
Рассмотрим математическую задачу, известную под названием «игра с выключателями света». Ее цель — нахождение лучших конфигураций включения и выключения для множества переключателей. Вот как это выглядит графически:
Представим, что у каждого переключателя есть вес, который мы не можем изменить. Мы можем включать (ON) или выключать (OFF) каждый переключатель. ON обозначает умножение на 1, а OFF — на -1. Затем мы складываем все веса переключателей, умноженные на их значения ON / OFF. Цель игры — установить переключатели для получения самого низкого значения суммы. Вес i-го выключателя обозначим через hi, а состояние переключателя через si. В зависимости от того, какие переключатели установлены на ON или OFF, мы получим разные итоговые суммы. Найти минимальную сумму будет легко, потому что есть простое правило для гарантированного минимума: Если мы установим все переключатели с положительными показателями в положение OFF, а все переключатели с отрицательными показателями — в положение ON, то в сумме получим самое низкое общее значение.Теперь усложним задачу: добавим новый вес J. Он будет изменяться в соответствии с состояниями ON/OFF соседних переключателей. А затем включен в итоговую сумму, которую мы получили ранее.
Теперь гораздо сложнее решить, должен ли выключатель быть включен или выключен, потому что его соседи влияют на него. Даже в простом примере с двумя переключателями мы не можем просто устанавливать параметр ON/OFF в положение, противоположное знаку собственного веса переключателей. Со сложной сетью выключателей задача становится практически нерешаемой. С помощью нескольких переключателей мы можем просто попробовать каждую комбинацию ON и OFF, есть только четыре возможности: [ON ON], [ON OFF], [OFF ON] или [OFF OFF]. Но по мере того, как мы добавляем все больше и больше переключателей, количество возможных способов установки переключателей растет экспоненциально: Как поможет квантовая механика? Мы начинаем с системы в ее квантовой суперпозиции, затем привлекаем квантовый компьютер (DWave), который, используя квантовую оптимизацию, находит для выключателей то состояние, в котором значение суммы будет самым низким.«Задача инкассатора»
Давайте сформулируем тестовую задачу и попробуем ее решить с помощью квантового компьютера DWave. Задача звучит так – у банка есть служба инкассации и множество банкоматов в городе, откуда нужно забрать деньги. Чем короче маршрут, тем меньше шансов попасть в неприятную ситуацию. Соответственно нам необходимо найти оптимальный маршрут во взвешенном направленном графе с N вершинами. Эта задача больше известна под именем «Задача коммивояжера» и не имеет лучшего варианта решения, чем полный перебор.Для того, чтобы решить эту задачу, нужно сначала понять, каким образом производится решение задач на DWave. Сначала мы должны разработать входной файл конфигурации. Он имеет следующий формат:
c c This is a sample .qubo file c with 4 nodes and 6 couplers c p qubo 0 4 4 6 c — 0 0 3.4 1 1 4.5 2 2 2.1 3 3 -2.4 c — 0 1 2.2 0 2 3.4 1 2 4.5 0 3 -2 0 2 3.4 1 2 4.5 0 3 -2 1 3 4.5678 2 3 -3.22
Через «с» обозначены строки с комментариями, далее мы задаем параметры программы в строке, начинающейся с символа «p». В этой строке мы задаем топологию (пока всегда 0), количество кубитов (в терминах игры со светом это «выключатели») и связей между парами (весы «J»). Далее идет блок с описанием весов каждого кубита. В этом блоке первые два числа должны быть одинаковыми, и они соответствуют номеру кубита. Следующий блок – блок весов связей между парами. Номер первого кубита должен быть всегда меньше второго.
Итак, разобравшись с форматом, приступим к решению нашей задачи.
Сначала мы выделим понятие шага пути – это набор всех возможных вершин графа, в которых мы можем находиться в текущий момент времени. Каждая вершина представлена кубитом. И таких шагов у нас будет N, где N – количество вершин в нашем графе.
Предположим, у нас всего 4 вершины, на каждом шаге мы можем находиться в одной из 4 вершин, соответственно весь набор кубитов разбивается на блоки по 4 кубита. В нашем случае из 4 вершин, нам нужен будет регистр из 16 кубитов, пронумеруем их – a0…a16. Соответственно, в первом блоке будут кубиты с номерами a0..a3 – они соответствуют нахождению в одной из вершин на первом шаге.
Теперь надо расставить веса кубитов и их связей внутри одного блока таким образом, чтобы только один кубит в каждом блоке в конечном решении оказался в состоянии 1, а остальные в 0. Это связано с тем, что в конечном итоге мы можем находиться только в одной из вершин на каждом шаге. Сделать это довольно просто – мы выставим вес каждого кубита в -1, а связи между ними в 2. Действительно, если мы посмотрим на формулу Σhisi + ΣJijsisj , то увидим, что минимальна она будет, если второе слагаемое будет равно нулю. А это произойдет только в двух случаях – если все кубиты равны 0 или если один любой находится в 1, а остальные в 0. Но при этом первое слагаемое даст минимум во втором случае.
Итак, мы выставляем таким образом веса на всех шагах (блоках из вершин) нашего пути. Теперь, если мы пошлем нашу программу на исполнение, нам придёт ответ вида (0001 0100 1000 1000). Для удобства мы разделили их на блоки по 4 кубита пробелами. Мы видим, что в каждом блоке только одна единичка, и ее номер в блоке соответствует номеру вершины. В нашем решении есть блоки с одинаковым номером вершины – 1000. Нам нужно исключить такие варианты решения, т.к. мы не можем возвращаться в уже пройденные вершины. Для того, чтобы сделать это, мы будем рассматривать новые блоки – объединяющие одну и ту же вершину на разных шагах.
Рассмотрим блок a0,a4,a8,a12. Эти кубиты соответствуют нахождению в первой вершине на соответствующем шаге. Аналогично предыдущему пункту, только один из них должен быть равен единице – тогда мы окажемся в первой вершине только один раз за весь путь. Расставляем веса связей для всех таких блоков и отправляем программу на исполнение. Получаем ответ вида (0001 0100 1000 0001 0010). Отлично, мы уже получили путь, соответствующий определению, теперь нужно найти оптимальный путь согласно весам ребер графа. Для этого мы берем значения из матрицы смежности графа и переносим эти значения в нашу конфигурацию. После этого получаем результат.
Решение до парсинга
Решение после парсинга
В действительности программирование на квантовом компьютере DWave немного сложнее, так как необходимо учитывать физическое разбиение всего регистра на блоки из 8 кубитов и т.д. Без этого некоторые из комбинаций могут быть не рассмотрены, и в результате мы получим некоторый локальный минимум вместо глобального, но даже такая простейшая программа дает по сравнению с классическими методами отличные результаты.
Мы провели пробный запуск на 14 вершинах на конкретном графе. Алгоритм перебора нашел кратчайший путь длиной 91, время работы заняло примерно 10 мин. Метод Литтла отработал почти мгновенно и дал результат 104. Квантовый алгоритм отработал тоже почти мгновенно и дал результат 97. При этом если программу на квантовом компьютере строить с учетом физических связей, то мы получим результат, аналогичный перебору.
Максимальный граф, который на данный момент мы можем обработать с помощью квантового вычислителя, содержит 44 вершины. На классическом вычислителе в общем случае это займет несоизмеримо большее количество времени, т.к. сложность растет по формуле n!..
Квантовый компьютер, построенный на принципах отжига, имеет большую мощность, чем существующие универсальные компьютеры, но при этом ограничен классом решаемых задач. У нас нет возможности задать первоначальные состояния кубитов или производить над ними какие-то унитарные преобразования – у нас есть только одна возможность – найти комбинацию, при которой значение функции Σhisi + ΣJijsisj при заданной конфигурации окажется минимальным. Однако даже с учетом этого ограничения квантовые компьютеры показывают существенный прирост производительности и могут быть эффективно использованы в задачах оптимизации.
Квантовые компьютеры сегодня
На данный момент существуют следующие основные направления реализации квантовых компьютеров:- На ионах в одномерном ионном кристалле в ловушке Пауля.
- В полупроводниковых кристаллах бесспинового моноизотопного кристалла кремния
- Кубиты на электронах в полупроводниковых квантовых точках.
- Кубиты на сверхпроводниковых мезоструктурах.
- На одиночных атомах в микрорезонаторах.
- С помощью линейных оптических элементов (оптический квантовый компьютер).
DWave имеет статус «аналогового квантового компьютера», так как способен решать лишь узкий круг задач квантового отжига. Но при этом его заявленная мощность составляет 2 000 кубитов.
IBM Q – это программа по разработке универсальных квантовых компьютеров, на которых можно исполнять произвольные квантовые алгоритмы. В данный момент работают системы из 20 кубитов (коммерческое использование), и открытые системы Q Experience на 16 и 5 кубитов. Q Experience cейчас, пожалуй, единственная открытая платформа, позволяющая разрабатывать квантовые алгоритмы. Она представляет собой набор атомарных гейтов, которые можно применять к кубитам.
Использование квантовых вычислений
Помимо описанных ранее сценариев, квантовые вычисления могут отлично работать в других сферах.Квантовая криптография. Защита информации основана на том, что задача расшифровки не решаема. Квантовая криптография основана на невозможности нарушить законы физики. Один из примеров – обмен секретными ключами BB84. Вася передает Маше набор квантовых частиц. Ревнивый злоумышленник Петя прослушивает канал связи и может перехватить частицы. Но для этого Пете придется измерить их. Он неминуемо разрушит их первоначальное состояние, что станет известно Васе и Маше.
Защита блокчейна. В принципе, она основана на том, что майнерам требуется большое количество времени, чтобы с помощью перебора найти число, при котором хеш блока меньше определенного порога. Это не позволяет подменить блок — пока новый хеш будет вычислен, цепочка уйдет далеко вперед. Квантовый блокчейн за счет параллелизма может мгновенно найти такое число, при котором хеш блока будет недосягаемо мал для классических вычислителей. Таким образом, атаковать сеть можно будет только при захвате 51% квантовых майнеров. А это выводит доверие на новый уровень – сговор более половины игроков с такими возможностями маловероятен.
Известно, что в 2014 году китайские исследователи впервые реализовали распознавание рукописного текста с помощью квантовых вычислений.
Наконец, мгновенная обработка колоссального объема данных и решение задач по оптимизации делают квантовые технологии одним из наиболее перспективных инструментов в области искусственного интеллекта и машинного обучения. По этой причине в 2013 году Google и NASA создали совместную лабораторию по исследованиям в этой области.
Подготовлено по материалам Дмитрия Сапаева, старшего руководителя направления по развитию ИТ-систем в отделе разработки ЦТИ Сбербанк-Технологий, и Дмитрия Булычкова, директора проектов в Центре технологических инноваций Сбербанка.
habr.com
Введение в квантовые вычисления / Блог компании Microsoft / Хабр
Статьи из цикла:
- Квантовые вычисления и язык Q# для начинающих
- Введение в квантовые вычисления
- Квантовые цепи и вентили — вводный курс
- Основы квантовых вычислений: чистые и смешанные состояния
- Квантовая телепортация на языке Q#
- Квантовые вычисления: справочные материалы
Введение
Как известно, идея квантовых вычислений была представлена Ричардом Фейнманом в 1981 году в ходе доклада на первой конференции «Физика вычислений» (Фейнман, 1982 г. — рекомендуется к ознакомлению). В ходе доклада Фейнман рассмотрел ряд сложностей, связанных с моделированием сложных квантовых систем с помощью классических компьютеров и выдвинул следующее предположение: чтобы достоверно моделировать квантовые системы, необходимо стремиться создать квантовые компьютеры.С тех пор сфера квантовых вычислений очень динамично развивалась. Сейчас мы уже вплотную подошли к подлинной физической реализации масштабируемого квантового компьютера (подробнее об этом — в следующих публикациях).
Наиболее фундаментальное различие между классическим компьютером и квантовым заключается в реализации бита. Бит (англ. bit, сокращение от «binary digit» — двоичное число) — минимальная единица цифровых данных. Классический бит в каждый конкретный момент времени может принимать лишь одно из двух значений: 0 или 1. Квантовый бит (кубит) подчиняется законам квантовой механики и поэтому может находиться в суперпозиции состояний 0 и 1.
Этим классическим состояниям 0 и 1 соответствуют обозначения Дирака |0〉 и |1〉, а формула состояния кубита выглядит так: .
Здесь — комплекснозначные коэффициенты, соответствующие требованию нормализации (это означает, что вероятность обнаружить кубит в одном из этих двух состояний равна 100 %, а вероятность обнаружить его в каком-либо другом состоянии равна 0 %). Поскольку , волновую функцию |ψ〉 можно переписать следующим образом:
Как оказывается, глобальная фаза не влияет на результаты экспериментов, и поэтому ее можно игнорировать. Однако локальная фаза остается, и волновая функция принимает следующий вид:
Записав ее в этой форме, мы можем представить суперпозицию состояний |0〉 и |1〉 в наглядном виде с помощью сферы Блоха:
Теперь любое унитарное преобразование волновой функции |ψ〉 можно представить как простое перемещение точки (она обозначена как |ψ〉) по поверхности сферы. Например, состоянию |ψ〉 = |0〉 соответствует точка на оси z, обозначенная на рисунке как |0〉. К сожалению, это наглядное представление подходит только для однокубитных состояний: простого обобщения для многокубитных систем пока не придумали. В этой серии статей мы еще вернемся к сфере Блоха.
Явления суперпозиции и запутанности* позволяют выполнять определенные операции с помощью квантовых компьютеров быстрее, чем это возможно (согласно современным представлениям) с помощью классических вычислительных систем. Примерами таких операций является разложение чисел на простые множители (Shor, 1997) и поиск по неструктурированным данным (Grover, 1997). Более того, благодаря этим уникальным квантовомеханическим особенностям появляются целые новые области науки и техники — например, квантовая криптография (Bennett & Brassard, 1984). В следующем разделе мы рассмотрим требования, которые предъявляются к таким системам.
*Суперпозицией называется явление, при котором состояние квантовой системы описывается вероятностным распределением возможных состояний одного кубита, например, . Для состояния запутанности необходимо два или более кубита (или, в более общем случае, степеней свободы). Это явление Эйнштейн охарактеризовал как «жуткое действие на расстоянии» — взаимосвязь двух частиц, при которой операция над одной из них может повлиять на состояние другой, вне зависимости от расстояния и физических барьеров между ними (однако запрет на передачу информации со сверхсветовой скоростью остается в силе). Примером состояния запутанности является состояние Белла:
Пять требований к квантовому компьютеру (и два дополнительных)
В 2008 году Давид Дивинченцо сформулировал пять условий (они представляют собой переработанную версию из статьи от 1996 г.), которым должна соответствовать система, чтобы считаться масштабируемым квантовым компьютером. Эти условия мы будем использовать в качестве основы для дальнейших обсуждений в этой серии публикаций. Ниже я привожу их общие формулировки (подробное обсуждение приводится в оригинальной статье).1. Физическая система должна быть масштабируемой, а состояние кубитов должно быть известным
Квантовый компьютер должен позволять увеличивать набор кубитов до количества, достаточного для сложных вычислений. «Хорошо описанным» называют кубит, свойства и взаимодействия которого с другими частями системы хорошо известны.2. Квантовый компьютер должен позволять надежно подготавливать наборы кубитов в простом начальном состоянии (например, |000…〉)
К началу вычислений система должна находиться в простом, точно известном состоянии. Если у нас нет возможности повторно приводить систему к этому простому начальному состоянию (инициализировать ее), то ее вообще нельзя считать вычислительной машиной.3. Система должна обладать достаточной долговечностью, чтобы выполнять операции над кубитами
По ряду причин (например, ввиду взаимодействия с внешними системами) систему кубитов сложно поддерживать в подготовленном состоянии достаточно долго до того, как она «декогерирует» из-за проявления нежелательных взаимодействий между системой и ее неизвестным и неуправляемым окружением. После декогеренции квантовой системы результаты измерений квантовых битов (0 и 1) будут описываться не квантовым распределением, а статистическим. Восстановить декогерированное состояние невозможно никакими квантовыми операциями. Поэтому период, за который система переходит в декогерентное состояние, должен быть намного больше времени, необходимого для выполнения операций на вентилях.4. Система должна позволять реализовать «универсальный набор» вентилей
Универсальным называется набор вентилей, достаточный для выполнения любого квантового вычисления. Вот минимальный необходимый набор операций: перемещение одиночных кубитов в любую точку на сфере Блоха (с помощью однокубитных вентилей) и запутывание компонентов системы (для этого нужны многокубитные вентили). Например, универсальным является набор, включающий вентиль Адамара, вентиль фазового сдвига, вентиль CNOT и вентиль π⁄8. С их помощью можно выполнить любое квантовое вычисление на произвольном наборе кубитов.5. Система должна поддерживать измерение отдельных кубитов
Необходимо иметь возможность получать результат вычислений путем считывания конечного состояния отдельных кубитов.Есть еще два дополнительных требования в отношении квантовой связи — они относятся к обработке квантовой информации:
- Система должна обладать способностью надежно преобразовывать данные, хранящиеся в виде стационарных (вычислительных) кубитов в сетевые (передающиеся) кубиты (например, фотоны) и обратно.
- Система должна обладать способностью корректно передавать сетевые кубиты между конечными точками.
В одной из последующих публикаций мы рассмотрим некоторые из этих потенциальных квантовых компьютеров, но вначале нужно познакомиться с квантовыми вентилями и диаграммами цепей. Именно им будет посвящена моя следующая статья. До следующей встречи!
Дополнительные ресурсы
habr.com
Кратчайшее введение в квантовые вычисления (гостевой пост Романа Душкина)
Сегодня я хотел бы начать публикацию серии заметок про эту животрепещущую тему, по которой недавно вышла моя новая книга, а именно введение в понимание квантовой вычислительной модели. Я благодарю моего доброго товарища и коллегу Александра за предоставленную возможность размещения в его блоге гостевых постов на эту тему.
Я постарался сделать эту кратчайшую заметку как можно более простой с точки зрения понимания неподготовленным читателем, который, однако, хотел бы понять, что такое квантовые вычисления. Тем не менее, от читателя требуется владеть базовым пониманием информатики. Ну и общее математическое образование тоже не помещало бы :). В статье нет формул, всё объясняется словами. Тем не менее, все вы можете задавать мне вопросы в комментариях, и я постараюсь объяснять, как только могу.
Что такое квантовые вычисления?
Начнём с того, что квантовые вычисления — это новая очень модная тема, которая там у них развивается семимильными шагами по нескольким направлениям (а у нас, как всякая фундаментальная наука пребывает в запустении и отдана на откуп нескольким учёным, сидящим в своих башнях из слоновой кости). И вот уже говорят о появлении первых квантовых компьютеров (D-Wave, но это не универсальный квантовый компьютер), ежегодно публикуются новые квантовые алгоритмы, создаются языки квантового программирования, сумрачный гений Международных Деловых Машин в тайных подземных лабораториях производит квантовые вычисления на десятках кубитов.
Что же это такое? Квантовые вычисления — это вычислительная модель, которая отличается от модели Тьюринга и фон Неймана, и предполагается, что для некоторых задач она является более эффективной. По крайней мере найдены задачи, для которых модель квантовых вычислений даёт полиномиальную сложность, в то время как для классической вычислительной модели неизвестно алгоритмов, которые имели бы сложность, ниже экспоненциальной (но, с другой стороны, пока ещё не доказано, что таких алгоритмов не существует).
Как такое может быть? Всё просто. Квантовая вычислительная модель основана на нескольких довольно простых правилах преобразования входной информации, которые обеспечивают массовую параллелизацию вычислительных процессов. Другими словами, можно одновременно вычислить значение функции для всех её аргументов (и это будет единственный вызов функции). Это достигается специальной подготовкой входных параметров и специальным же видом функции.
Светитель Проц учит, что всё это суть синтаксическая манипуляция с математическими символами, за которой, по сути, нет никакого смысла. Есть формальная система с правилами преобразования входа в выход, и эта система позволяет при помощи последовательного применения этих правил получать из входных данных выходные. Всё это в конечном итоге сводится к перемножению матрицы и вектора. Да, да, да. Вся модель квантовых вычислений основана на одной простой операции — умножении матрицы на вектор, в результате чего на выходе получается другой вектор.
Светитель Халикаарн в противоположность учит, что существует объективный физический процесс, который выполняет указанную операцию, и только лишь существование которого и обуславливает возможность массовой параллелизации вычислений функции. То, что мы воспринимаем это как умножение матрицы на вектор, является всего лишь способом нашего далеко не совершенного отражения объективной реальности в нашем разуме.
Мы в нашей научной лаборатории имени светителей Проца и Халикаарна объединяем эти два подхода и говорим, что модель квантовых вычислений есть математическая абстракция, которая отражает объективный процесс. В частности, числа в векторах и матрицах являются комплексными, хотя это совершенно не увеличивает вычислительную мощность модели (она бы была такой же мощной и с действительными числами), однако выбраны именно комплексные числа потому, что найден объективный физический процесс, который осуществляет такие преобразования, как описывает модель, и в котором используются именно комплексные числа. Этот процесс называется унитарной эволюцией квантовой системы.
В основе квантовой вычислительной модели лежит понятие кубита. Это практически то же самое, что и бит в классической теории информации, однако кубит может одновременно принимать несколько значений. Говорят, что кубит находится в суперпозиции своих состояний, то есть значение кубита есть линейная комбинация его базовых состояний, и коэффициенты при базовых состояниях как раз являются комплексными числами. Базовыми же состояниями являются известные по классической теории информации значения 0 и 1 (в квантовых вычислениях их принято обозначать |0> и |1>).
Пока не очень-то и понятно, в чём фишка. А фишка вот в чём. Суперпозиция одного кубита записывается как A|0> + B|1>, где A и B — некоторые комплексные числа, единственное ограничение на которые заключается в том, что сумма квадратов их модулей всегда должна равняться 1. А если рассмотреть два кубита? Два бита могут получать 4 возможных значения: 00, 01, 10 и 11. Резонно предположить, что два кубита представляют собой суперпозицию четырёх базовых значений: A|00> + B|01> + C|10> + D|11>. И так оно и есть. Три кубита представляют собой суперпозицию восьми базовых значений. Другими словами, квантовый регистр из N кубитов одновременно хранит в себе 2N комплексных чисел. Ну а с математической точки зрения это есть 2N-мерный вектор в комплекснозначном пространстве. Именно этим достигается экспоненциальная мощность модели квантовых вычислений.
Далее функция, которая применяется к входным данным. Поскольку теперь входные данные представляют собой суперпозицию всех возможных значений входного аргумента, функция должна быть преобразована в такой вид, чтобы принять такую суперпозицию и обработать её. Тут тоже всё более или менее просто. В рамках модели квантовых вычислений каждая функция представляет собой матрицу, на которую накладывается одно ограничение — она должна быть эрмитовой. Это значит, что при умножении этой матрицы на свою эрмитово-сопряжённую, должна получиться единичная матрица. Эрмитово-сопряжённая матрица получается при помощи транспонирования исходной матрицы и заменой всех её элементов на их комплексно-сопряжённые. Это ограничение следует из упомянутого ранее ограничения на квантовый регистр. Дело в том, что если такую матрицу умножить на вектор квантового регистра, то в результате получится новый квантовый регистр, сумма квадратов модулей комплекснозначных коэффициентов при квантовых состояниях которого всегда равна 1.
Показано, что любую функцию можно специальным образом преобразовать в такую матрицу. Также показано. что любую эрмитову матрицу можно выразить посредством тензорного произведения небольшого набора базисных матриц, представляющих базисные логические операции. Тут всё примерно так же, как в классической вычислительной модели. Эта более сложная тема, которая выходит за рамки данной обзорной статьи. То есть сейчас главное понять — любая функция может быть выражена в виде матрицы, подходящей для использования в рамках модели квантовых вычислений.
Что происходит дальше? Вот у нас есть входной вектор, который представляет собой суперпозицию различных вариантов значений входного параметра функции. Есть функция в виде эрмитовой матрицы. Квантовый алгоритм представляет собой умножение матрицы на вектор. В результате получается новый вектор. Что же это за ерунда-то такая?
Дело в том, что в модели квантовых вычислений есть ещё одна операция, которая называется измерением. Мы можем измерить вектор и получить из него конкретное значение кубита. То есть суперпозиция схлопывается в конкретное значение. И вероятность получения того или иного значения равна квадрату модуля комплекснозначного коэффициента. И теперь понятно, почему сумма квадратов должна равняться 1, поскольку при измерении всегда будет получено какое-то конкретное значение, а потому сумма вероятностей их получения равна единице.
То есть что получается? Имея N кубитов можно одновременно обработать 2N комплексных чисел. И в выходном векторе будут результаты обработки всех этих чисел одновременно. В этом мощь модели квантовых вычислений. Но получить можно только одно значение, и оно может быть каждый раз различное в зависимости от распределения вероятностей. В этом ограничение модели квантовых вычислений.
Суть квантового алгоритма заключается в следующем. Создаётся равновероятностная суперпозиция всех возможных значений входного параметра. Эта суперпозиция подаётся на вход функции. Далее по результатам её выполнения делается вывод о свойствах этой функции. Дело в том, что мы не можем получить все результаты, но вот сделать выводы о свойствах функции можем вполне. И в следующем разделе будут показаны несколько примеров.
Пара интересных квантовых алгоритмов
В подавляющем большинстве источников по квантовым вычислениям читатель найдёт описания нескольких алгоритмов, которые, собственно, обычно используются для демонстрации мощи вычислительной модели. Здесь мы тоже кратко и поверхностно рассмотрим такие алгоритмы (два из них, которые демонстрируют различные базовые принципы квантовых вычислений). Ну а для детального ознакомления с ними опять адресую к своей новой книге.
Алгоритм Дойча
Это первый алгоритм, который был разработан для того, чтобы показать суть и эффективность квантовых вычислений. Задача, которую решает этот алгоритм, совсем оторвана от реальности, однако на ней как раз можно показать базовый принцип, положенный в основу модели.
Итак, пусть есть некоторая функция, которая получает на вход один бит и возвращает на выходе тоже один бит. Честно говоря, таких функций может быть всего 4. Две из них являются константными, то есть одна всегда возвращает 0, а другая всегда возвращает 1. Две другие являются сбалансированными, то есть возвращают 0 и 1 в равных количествах случаев. Вопрос: как за один вызов этой функции определить, константная она или сбалансированная?
Очевидно, что в классической вычислительной модели этого сделать нельзя. Необходимо дважды вызвать функцию и сравнить результаты. А вот в модели квантовых вычислений это сделать можно, поскольку функция будет вызвана только один раз. Посмотрим…
Как уже было написано, мы подготовим равновероятностную суперпозицию всех возможных значений входного параметра функции. Поскольку на входе у нас один кубит, то его равновероятностная суперпозиция готовится при помощи одного применения гейта Адамара (это такая специальная функция, которая и готовит равновероятностные суперпозиции :). Далее снова применяется гейт Адамара, который работает таким образом, что если ему на вход подаётся равновероятностная суперпозиция, то он преобразует её назад в состояния |0> или |1> в зависимости от того, в какой фазе находится равновероятностная суперпозиция. После этого производится измерение кубита, и если он равен |0>, то рассматриваемая функция константна, а если |1>, то сбалансирована.
Что получается? Как уже было сказано, при измерении мы не можем получить все значения функции. Но мы можем сделать определённые выводы о её свойствах. Задача Дойча как раз и спрашивает о свойстве функции. И это свойство очень простое. Ведь как выходит? Если функция константна, то сложение по модулю 2 всех её выходных значений всегда даёт 0. Если же функция сбалансирована, то сложение по модулю 2 всех её выходных значений всегда даёт 1. Именно этот результат мы и получили в результате выполнения алгоритма Дойча. Мы не знаем, какое именно значение вернула функция на равновероятностной суперпозиции всех входных значений. Мы знаем только, что это тоже суперпозиция результатов, и если теперь эту суперпозицию преобразовать специальным образом, то будут сделаны однозначные выводы о свойстве функции.
Вот как-то так.
Алгоритм Гровера
Другой алгоритм, который показывает квадратичный выигрыш по сравнению с классической вычислительной моделью, решает более приближённую к реальности задачу. Это алгоритм Гровера, или, как называет его сам Лов Гровер, алгоритм поиска иголки в стоге сена. Этот алгоритм основан на другом принципе, лежащем в основе квантовых вычислений, а именно амплификации.
Уже упоминалась некая фаза, которая может быть у квантового состояния в составе кубита. Как таковой фазы нет в классической модели, это что-то новенькое именно в рамках квантовых вычислений. Фазу можно понимать как знак у коэффициента при квантовом состоянии в суперпозиции. Алгоритм Гровера основан на том, что специально подготовленная функция меняет фазу у состояния |1>.
Алгоритм Гровера решает обратную задачу. Если есть неупорядоченый набор данных, в котором надо найти один элемент, удовлетворяющий критерию поиска, алгоритм Гровера поможет это сделать эффективнее, чем простой перебор. Если простой перебор решает задачу за O(N) обращений к функции, то алгоритм Гровера эффективно находит заданный элемент за O(√N) обращений к функции.
Алгоритм Гровера состоит из следующих шагов:
1. Инициализация начального состояния. Опять готовится равновероятностная суперпозиция всех входных кубитов.
2. Применение итерации Гровера. Данная итерация состоит из последовательного применения функции поиска (она определяет критерий поиска элемента) и специального гейта диффузии. Гейт диффузии меняет коэффициенты при квантовых состояниях, вращая их вокруг среднего. Тем самым производится амплификация, то есть увеличение амплитуды искомого значения. Фишка в том, что осуществить применение итерации необходимо определённое количество раз (√2n), иначе алгоритм вернёт не те результаты.
3. Измерение. После измерения входного квантового регистра с большой вероятностью будет получен искомый результат. Если необходимо увеличить достоверность ответа, то алгоритм прогоняется несколько раз и вычисляется совокупная вероятность правильного ответа.
Интерес в данном алгоритме представляет то, что он позволяет решить произвольную задачу (например, любую из класса NP-полных), предоставляя пусть и не экспоненциальное, но существенное повышение эффективности по сравнению с классической вычислительной моделью. В одной из будущих статей будет показано, как это можно сделать.
Квантовый зоопарк
Тем не менее, уже нельзя говорить о том, что учёные продолжают сидеть в своей башне из слоновой кости. Несмотря на то, что многие квантовые алгоритмы разрабатываются для каких-то странных и непонятных матаноподобных задач (например, определение порядка идеала конечного кольца), уже разработан ряд квантовых алгоритмов, которые решают очень даже прикладные задачи. В первую очередь это задачи из области криптографии (компрометация различных криптографических систем и протоколов). Далее идут типовые математические задачи на графах и матрицах, при этом такие задачи имеют очень большую область применения. Ну и есть ряд алгоритмов аппроксимации и эмуляции, которые используют аналоговую составляющую модели квантовых вычислений.
В сети Интернет по адресу http://math.nist.gov/quantum/zoo/ ведётся полный список квантовых алгоритмов. Его версия, актуальная на 05.09.2011, в переведённом виде имеется в уже неоднократно упомянутой моей книге. Здесь нет смысла перечислять все эти многочисленные алгоритмы, которых уже более 50. Приведём лишь диаграмму отношений квантовых алгоритмов и задач (кликабельно, 871 Кб):
На представленной диаграмме прямоугольником обозначается квантовый алгоритм или задача, которая может быть решена в рамках модели квантовых вычислений. Для каждого алгоритма и задачи приводятся две характеристики — ускорение и типы задач, решаемых алгоритмом (или тип самой задачи). Наконец, между алгоритмами и (или) задачами рассматриваются четыре типа отношений, а именно:
- Если из алгоритма A идёт обычная стрелка в алгоритм B, то это значит, что алгоритм B основан на алгоритме A.
- Если же стрелка пунктирная, то алгоритм B сводится к алгоритму A, то есть это в большей мере отношение подобия.
- Волнистая стрелка обозначает, что алгоритм A решает прикладную задачу B.
- Наконец, двойная линия между прямоугольниками без стрелок обозначает, что два алгоритма сходны между собой.
Заключение
В заключение хотелось бы ещё раз поблагодарить хозяина этого блога, а также сообщить, что всё, что написано в этой краткой заметке, более подробно (и даже в некоторых местах использованы математические формулы довольно жуткого вида) написано у меня в книге «Квантовые вычисления и функциональное программирование», которую всякий желающий может свободно скачать и прочитать.
Я буду рад получить комментарии и замечания. Ваши вопросы задавайте здесь или присылайте мне на почту. Постараюсь на всё ответить и всё разъяснить. Дерзайте!
Дополнение: Алгоритм Шора, его реализация на языке Haskell и результаты некоторых опытов
Метки: Алгоритмы, Параллелизм и многопоточность.
eax.me
Квантовые вычисления — все что вы не могли понять и стеснялись спросить — CloudCoin
Внимание! Научно-популярный лонгрид об одной из самых актуальных тем современности — квантовых вычислениях, квантовых компьютерах и о том, что нас ждет в будущем.
Почему нас так интересует эта тема? Потому что блокчейн основан на алгоритмах шифрования, принцип работы и распространения криптовалют лежит на использовании вычислительных мощностей майнеров. Квантовые компьютеры перевернут этот мир с ног на голову.
Поэтому устраивайтесь поудобнее и запаситесь временем.
Квантовые вычисления для любопытных
Это несложно понять, но сложнее представить
Возможно вы уже слышали о квантовых вычислениях и квантовых компьютерах, это должно быть интересно, но совершенно не понятно как это работает и что вообще означает. На самом деле что угодно квантовое кажется слишком сложным.
На самом деле это не так. Проблема в том, что все написанное о квантовых вычислениях в технических и научно-популярных журналах представляет собой полную чушь.
Вот стандартное объяснение что это такое:
В обычных вычислениях компьютеры оперируют триггерами — битами, которые имеют бинарное значение 0 или 1. За счет сочетания множества битов можно хранить данные или выполнять инструкции. Все это происходит в обычных компьютерах, мобильных телефонах, в калькуляторах.
В квантовых компьютерах триггеры иного рода, каждый из них представляет несколько значений одновременно.
Вот например объяснение от премьер-министра Канады (полагаем, достаточно авторитетное):
Обычные компьютеры работают очень просто — в зависимости от того, идет ли ток по проводнику или нет — бит принимает значение 0 или 1. Для квантового состояния в один бит возможно поместить намного больше информации, квантовое состояние намного сложнее, потому как мы можем наблюдать дуализм представления в виде частицы или волны.
Значения кубитов (квантовых битов) основываются на квантовом эффекте суперпозиции (здесь можно привести в качестве примера кота Шреддингера). Кроме этого, бывает другой квантовый эффект, который называется неопределенностью, он позволяет связывать кубиты между собой. Если поместить кубиты в состояние суперпозиции и связать между собой, то кубиты синхронизируются. Даже если они расположены в разных частях вселенной — изменение состояния одного кубита приводит к изменению состояния других, таким образом, все связанные (спутанные) кубиты танцуют в унисон. Эйнштейн от такого эффекта откровенно ужаснулся.
Не смотря на такой невообразимый ужас, когда кубиты выстраиваются таким образом, то возможно производить множество вычислений одновременно. Внимание! Не со скоростью света, с которой распространяется магнитное поле в традиционных триггерах и битах, а моментально и одновременно.
Обычный компьютер производит вычисления примерно также, как вы пытаетесь выбраться из лабиринта — перебираете по очереди все возможные ходы, упираясь в тупики, возвращаясь и продвигаясь вперед до тех пор, пока не найдете выход.
Квантовый компьютер может проверить все возможные ходы за раз. Кубиты представляют собой все возможные значения вероятностей. Чем больше кубитов — тем больше вероятностей, точно также как в лабиринте — чем больше лабиринт, тем больше в нем ходов, тем сложнее из него выбраться.
Если соединить 1000 кубитов в суперпозиции, то это позволит представить все числа от 1 до 10 в 300 степени. Для сравнения, видимая часть вселенной содержит от 10 в 78 до 10 в 82 степени атомов.
Сложно да? На этом месте обычно мозг начинает взрываться.
А журналисты, которые пишут в научпоп-журналы, на этом месте начинают заблуждаться. Они пишут, что квантовые компьютеры дадут нам возможности для создания умопомрачительных телефонов, научат безошибочно предсказывать погоду, котировки акций и пробки на дорогах, создавать искусственный интеллект и творить мир во всем мире. Но к сожалению, это все — полная чушь.
Проблемы начинаются тогда, когда вы попытаетесь измерить, что происходит с кубитом, описать или обозначить его состояние, открыть ящик с котом Шредингера.
Представьте уличного наперсточника, только у него не три наперстка, а тысяча. И шарик не один, и вообще вместо шарика под наперстком может быть орешек или ягодка. Когда все наперстки перевернуты вверх дном, то комбинация орешков и ягодок под ними может быть какой угодно, особенно если мы точно не зафиксировали количество орешек и ягодок. Могут быть все орешки, могут быть все ягодки, а могут быть и те и другие в произвольном соотношении. Так они находятся в состоянии суперпозиции. Раскрывая наперстки — мы видим всю картину, количество и порядок орешков и ягодок. Изначально при перевернутых наперстках у вас было множество вероятностных комбинаций, но как только вы их раскрыли — результат представляет собой набор случайных значений. То же самое можно проделать на обычном компьютере или бросая монетку.
О следующем вы наверняка не читали в научпоп-журналах. Штука в том, что кубит не находится в состоятии 0 и 1 одновременно, такого нет. Вместо этого кубит представляет собой градиент численных значений — амплитуду вероятностей, они представляют собой положительные, отрицательные и комплексные значения. Визуально кубит можно представить в виде сферы (см. рис)
В состоянии связанности и суперпозиции кубиты представляют собой квантовый регистр. В ходе вычислений в квантовом регистре происходит выстраивание амплитуд кубитов таким образом, что положительные значения амплитуды одних кубитов нейтрализуют отрицательные амплитуды других кубитов, таким образом происходит отмена неверных вычислений (положительные амплитуды кубитов наоборот усиливают друг друга), таким образом вырисовываются пути, ведущие к правильному ответу.
Этот процесс можно представить в виде множества разных паттернов волн в океане, которые в конечном итоге собираются в одно течение, ведущее к правильному ответу. Потому как мы не знаем решения заранее, то найти его — не значит найти какой-то один правильный поток в этом океане (как например можно найти правильный путь из лабиринта), а скорее сформировать его из целого набора волн, которые вместе приводят к одному большому всплеску. То есть, океан — это не набор ходов лабиринта, которые уже сформированы, они формируются в ходе решения задачи, волны перемешиваются между собой, складываются друг с другом и нейтрализуются, приводя тем самым к решению.
Теперь понятна умозрительная картина?
Сейчас будет еще сложнее и вы окончательно запутаетесь.
Кубит — будто вздорная девица, которой все кругом мешают, поэтому ее нужно держать в покое и уединении. Если будет замечена легкая вибрация от соседнего атома — кубит разгневается и выйдет из состояния суперпозиции. Поэтому основная сложность заключается в поддержании деликатного состояния суперпозиции и спутанности кубитов в течение промежутка времени, достаточного для проведения вычислений. Этот промежуток времени называется временем когерентности.
Другими словами, квантовые вычисления — это не просто совершенно новый способ проведения расчетов, но еще и невероятно сложная задача в инженерном плане.
Это не значит, что квантовые вычисления позволят смартфонам работать быстрее или приведут к новому поколению голосовых команд и ассистентов. Они не помогут лучше играть в Го или шахматы, рассчитывать полеты самолетов или доказывать теоремы. Во многих подобных случаях квантовые компьютеры способны сделать намного меньше, чем от них ожидают.
Зачем тогда их создавать вообще? Особенно учитывая тот фактор, что создание квантового компьютера, подходящего для решения прикладных задач, — это крайне сложная технология. И ведь над ней активно работает множество инженеров и ученых по всему миру. Зачем?
А причина в том, что существует два особенных типа задач, которые квантовые компьютеры способны решать лучше всего.
Первый тип — это задачи криптографии, крайне перспективная и денежная отрасль, которая запустит бизнес на квантовых компьютерах. На сегодняшний день многие системы шифрования основываются на перемножении больших чисел и их поиске для того, чтобы получить взломостойкий шифр. Квантовый компьютер способен проделывать подобные операции намного быстрее. Самый большой интерес заключается в возможности дешифрования данных. В настоящий момент безопасность шифрования заключается в том, что на расшифровку данных требуются несоизмеримо большие вычислительные мощности и огромное время, измеряемое в тысячелетиях. Квантовые компьютеры способны раскрыть такой шифр намного быстрее, примерно за то же время, что затрачено на само шифрование. Именно поэтому банковские и технологические компании, а также шпионы вкладывают огромные деньги в развитие квантовых вычислений.
Второй тип задачи заключается в том, что квантовые компьютеры способны эмулировать различные квантовые системы. И именно эта возможность вероятно перевернет наше представление о биологических системах, сверхпроводимых материалах, или выведет на новый уровень понимания квантовой химии, не говоря уже о самой квантовой физике.
Есть ли опытные образцы?
В начале мая 2017 года исследователи разработали программируемый квантовый компьютер, состоящий из шести кубитов, а также несколько нестабильных экспериментальных образцов, состоящих из 10-20 кубитов. Исследователи уверенны в том, что при разработке квантовых компьютеров, состоящих из 30-100 кубитов, их можно выводить в коммерческое использование, и вероятно это произойдет в ближайшие пару лет. Наиболее многообещающими выглядят проекты Microsoft, IBM, Оксфордского университета и возможно нескольких лабораторий в Китае. Однако, судя по всему в лидерах будет проект команды Google, работающей под началом Джона Мартиниса. Среди их последних разработок есть чип, состоящий из шести кубитов, выстроенных в ряд 2х3.
Кроме этого, есть компания D-Wave, которая часто фигурирует в заголовках различных изданий. В начале этого года они заявили о том, что построили квантовый компьютер, состоящий из 2000 кубитов. Однако, разработанный ими процессор основывается лишь на квантовом эффекте, поэтому он не может считаться настоящим квантовым компьютером. Основа технологии — это процесс так называемого отжига, происходящий во множестве сверхпроводящих петель магнитного поля, которые взаимодействуют друг с другом. Как это происходит — когда энергия магнитных полей высокая, то сверхпроводящие петли взаимодействуют друг с другом, легко переключая свою полярность туда и обратно. Как только энергия магнитного поля уменьшается — магниты начинают принимать какое-либо определенное значение до тех пор, пока энергия магнитного поля не снизится до минимального уровня. После этого магниты стабильны и каждый имеет одно значение, которое можно считать, это и есть результат вычисления.
Технически эти петли магнитного поля нельзя считать кубитами, они не находятся в состоянии запутанности, их квантовое состояние гораздо более хрупкое, а результаты вычислений неточны. Однако, если даже такая технология может иметь практическое применение, то и сомнений никаких не остается, что квантовые компьютеры способны решать практические задачи экспоненциально быстрее, чем обычные компьютеры.
D-Wave выбрала стратегию в получении максимального количества кубитов как можно быстрее, не особо заботясь об исправлении ошибок и корректности работы. У них получился достаточно грязный результат, зато быстро. Другие же исследователи пытаются добиться чистого результата. D-Wave пошли на огромный риск за счет того, что стали первыми в коммерческом использовании компьютеров, основанных на квантовом эффекте, волновая система, которую они используют — просто эмулирует квантовые вычисления. Однако, даже такое решение — это несколько больше, чем просто появление еще одного мощного компьютера.
Квантовые компьютеры — это не совсем о технологиях, как например разработка гаджетов виртуальной реальности или нового микрочипа. Это — научное решение, наподобие Большого Адронного Коллайдера или расшифровки генотипа. Если проблема разработки квантовых компьютеров будет решена, то большая часть зашифрованных данных в мире может быть расшифрована. Алгоритм шифрования RSA потеряет свое значение, блокчейн окажется раскрытым и прозрачным для каждого, произойдет революция (или девальвация) в криптографии.
Но кроме этого, появится возможность в эмуляции жизни вселенной в масштабе одного атома, могут быть получены важные открытия о квантовой гравитации и многом другом. И это действительно важные применения квантовых компьютеров.
Поэтому, если вы увидите заголовки в СМИ, повествующих о том, что какой-либо банк инвестировал в развитие квантовых вычислений, или же какая-либо лаборатория в Китае добилась превосходства в проектировании квантовых компьютеров — копайте глубже. Возможно дело обстоит совсем иначе, и суть открытий лежит в иной области.
Проблема квантовых вычислений — одна из самых интересных задач в современной науке. Обычно человечество изобретает новые механизмы для подтверждения гипотез, однако разработка масштабируемого квантового компьютера приведет к открытию невообразимых вычислительных мощностей вселенной прямо на поверхности.
cloudcoin.ru
Квантовые вычисления Википедия
Квантовый компьютер — вычислительное устройство, которое использует явления квантовой механики (квантовая суперпозиция, квантовая запутанность) для передачи и обработки данных. Квантовый компьютер (в отличие от обычного) оперирует не битами (способными принимать значение либо 0, либо 1), а кубитами, имеющими значения одновременно и 0, и 1. В результате можно обрабатывать все возможные состояния одновременно, достигая гигантского превосходства над обычными компьютерами в ряде алгоритмов[1].
Полноценный универсальный квантовый компьютер является пока гипотетическим устройством, сама возможность построения которого связана с серьёзным развитием квантовой теории в области многих частиц и сложных экспериментов; разработки в данной области связаны с новейшими открытиями и достижениями современной физики. На середину 2010-х были практически реализованы лишь единичные экспериментальные системы, исполняющие фиксированный алгоритм небольшой сложности.
Первым практическим высокоуровневым языком программирования для такого вида компьютеров считается язык Quipper[en], основанный на Haskell[2] (см. Квантовое программирование).
Введение[ | код]
Идея о квантовых вычислениях была высказана Юрием Маниным в 1980 году[3].
Одна из первых моделей квантового компьютера была предложена[4]Ричардом Фейнманом в 1981 году. Вскоре Пол Бениофф описал теоретические основы построения такого компьютера[5].
Также концепцию квантового компьютера в 1983 году предлагал Стивен Визнер в статье, которую он пытался опубликовать в течение более десяти лет до этого[6][7].
Необходимость в квантовом компьютере возникает тогда, когда мы пытаемся исследовать методами физики сложные многочастичные системы, подобные биологическим. Пространство квантовых состояний таких систем растет как экспонента от числа n{\displaystyle n} составляющих их реальных частиц, что делает невозможным моделирование их поведения на классических компьютерах уже для n=10{\displaystyle n=10}. Поэтому Визнер и Фейнман высказали идею построения квантового компьютера.
Квантовый компьютер использует для вычисления не обычные (классические) алгоритмы, а процессы квантовой природы, так называемые квантовые алгоритмы, использующие квантовомеханические эффекты, — такие как квантовый параллелизм и квантовая запутанность.
Если классический процессор в каждый момент может находиться ровно в одном из состояний |0⟩,|1⟩,…,|N−1⟩{\displaystyle |0\rangle ,|1\rangle ,\ldots ,|N-1\rangle }
ru-wiki.ru
Квантовые вычисления / Наука / Лента.co
Читать оригинал публикации на postnauka.ru
Физик Сет Ллойд о странной квантовой механике, кубитах и концепции компьютера
Квантовый компьютер представляет собой устройство, которое хранит и обрабатывает информацию на уровне отдельных атомов и элементарных частиц. У квантовых вычислений есть два аспекта: первый — квантовый, а второй — вычислительный. «Квантовая механика» — это звучит немного странно, и квантовая механика действительно необычна с научной точки зрения. Но в каком-то смысле квантовый аспект понять проще. Квантовая механика — это физическая теория, которая объясняет, как ведут себя вещи на самом маленьком и фундаментальном уровне. Это раздел физики, который изучает, как атомы, фотоны (частицы света), электроны, элементарные частицы ведут себя. Если мы собираемся построить компьютер на уровне атомов и масштабе элементарных частиц, он неизбежно будет работать по законам квантовой механики. И мы увидим, что странность квантовой механики, тот факт, что квантовая механика является странной и нелогичной, на самом деле позволяет нам производить вычисления способом, недоступным для ноутбука или iPhone.
Для выполнения вычислений компьютер, располагая информацией, разбитой на мельчайшие кусочки, манипулирует ими, заставляет их взаимодействовать и изменяет их по предельно общим правилам. На самом деле существует понятие универсальных цифровых вычислений, охватывающее наиболее сложные задачи, которые способен решить классический компьютер, систематически оперируя битами. Таким образом, квантовый компьютер — это компьютер, который берет биты и работает с ними систематическим образом, но работает на уровне атомов, элементарных частиц, фотонов (частиц света), электронов — там, где царят законы квантовой механики.
Квантовая механика странная. Странная — это научный термин. Нильс Бор, один из основателей квантовой механики, сказал:
«Любой, кто говорит, что понимает квантовую механику и у него от нее не кружится голова, на самом деле не понял ее».
Вообще говоря, на датском это впечатляет еще больше. Но это правда: квантовая механика странная и нелогичная. Чтобы прочувствовать эту странность, подумайте о том, что называется корпускулярно-волновым дуализмом. Я знаю, звучит замысловато — корпускулярно-волновой дуализм. Что это вообще значит? Это значит, что то, о чем мы думаем как о частицах, например атомы или электроны, имеет волну, связанную с ним. Подобным же образом то, о чем мы думаем как о волнах, например свет или звук, имеет связанные с ним частицы. Все это происходит на самом микроскопическом уровне. Это означает, что, когда вы храните бит информации на квантовом компьютере, скажем, на позиции электрона, этот электрон имеет также связанную с ним волну.
В классическом компьютере бит хранится следующим образом: в случае нуля — это низкое напряжение — куча электронов «здесь»; единица — это высокое напряжение — куча электронов «там». Теперь давайте уменьшать масштаб до того момента, когда мы получим квантовый бит, то есть один электрон. Так, нуль — один электрон в одном месте, единица — это один электрон в другом. Прекрасно, представьте: электрон здесь означает нуль, вы переместите его туда — он становится единицей, вы переместите его сюда — он становится снова нулем. У вас есть два электрона, вы перемещаете их туда-сюда, вы изменяете несколько битов — нет никаких проблем с хранением и обработкой информации на уровне отдельных электронов.
Проблема в том, что электрон — это квантово-механический объект и, хотя он является частицей, также имеет волну, связанную с ним. Эта волна имеет непосредственное отношение к тому, где электрон находится. Если волна электрона полностью находится в каком-то одном месте, то и электрон находится там же, и это будет нуль. Если волна электрона полностью тут, то электрон тоже находится тут, и это будет единица.
Но забавно в квантовой механике то, что волны не должны быть только здесь или только там. Знаете, они вообще не должны быть только в каком-то одном месте. Волны — протяженные объекты, и в ряде случаев они могут одновременно находиться и там, и здесь.
Что это значит, что электрон, как волна, находится и там, и здесь? Это означает, что этот один электрон находится одновременно в двух местах. Таким образом, квантовый бит, или кубит, как его иногда называют, обладает забавным качеством: он может быть сразу и нулем, и единицей, потому что этот электрон одновременно в двух местах. Это просто странно и контринтуитивно. Нет классического образа, который бы это иллюстрировал. Например, какой-нибудь футбольный мяч не может быть здесь и там одновременно, даже если неразбериха на поле может иногда создавать такое впечатление. Так что, поскольку электрон может быть параллельно в двух местах, квантовый бит, или кубит, может быть одновременно нулем или единицей. Таким образом, эта главная особенность квантовой странности — корпускулярно-волновой дуализм, загадочный, нелогичный и трудно поддающийся обычному мышлению, — означает, что квантовые биты могут иметь значения нуль и единица одновременно. А это значит, что квантовым компьютерам доступны способы вычисления, невозможные на классических компьютерах.
Можно думать об этом так: если классическое вычисление — это последовательность изменений битов несколько раз туда-обратно, вы можете представить себе это как волну, одну волну, как протяженную ноту («ааааааааа») или как один напев («а-а-а-а-а-а»). Таким образом, каждое из классических вычислений подобно одной волне, состоящей из серии чистых нот. В квантовых вычислениях, наоборот, волны всех битов могут иметь несколько значений сразу, так что это симфония. Я не могу спеть симфонию в одиночку, но вы можете себе ее представить. И что происходит в случае квантовых вычислений, так это то, что волны, соответствующие каждому из вычислений, складываются таким образом, что между ними возникает интерференция и гармония. Благодаря этому возможности, которые открываются перед квантовым компьютером, несравненно больше, чем возможности классического компьютера.
Итак, давайте подумаем, какое назначение имеет бит внутри компьютера. Если у меня есть нуль или единица, бит может быть информацией. Нуль и единица — это звучит так прозаично. Положим, я спрашиваю мою невесту или мою подругу: «Ты выйдешь за меня?» И она в ответ пришлет мне бит информации, где нуль — это «нет», а единица — «да». Это очень важный бит для меня, и, возможно, она отвечает мне через почту, что, наверное, не самый хороший способ принять предложение руки и сердца. Для квантового брака она может отправить квантовую суперпозицию нуля и единицы — это означает, что она испытывает двойственные чувства в квантово-механическом смысле. Так что же произойдет, когда я на самом деле посмотрю на ее ответ? Эти квантовые биты имеют такое свойство, что если у вас есть бит с нулем и единицей, где нуль — это «нет», а единица — «да», в одно и то же время, то мне надо будет посмотреть, есть ли здесь электрон. Нет. А здесь есть? Да. И тогда половину времени я получу ответ «нет», а половину времени — «да». Так что если бы моя подруга дала мне такой ответ, то это было бы, по сути, равносильно бросанию монетки, чтобы решить, что ответить на мое предложение.
По сути, квантовые вычисления производятся благодаря интерференции между этими различными частями — это как когда мы слышим два звука, доносящиеся до нас в одно и то же время, мы воспринимаем не каждый из них по отдельности, но оба этих звука в совокупности, интерферирующие друг с другом. Это может казаться волшебством, как при построении квантовых компьютеров вы используете компоненты атомного масштаба, получаются очень-очень маленькие приспособления, и вам стоит следить за ними, потому что, если вы один такой потеряете, вы никогда его снова не увидите. И вы можете спросить: «Зачем нам все это делать, когда у нас есть прекрасные классические компьютеры?»
Идея квантовых вычислений, хранения битов на отдельных атомах была предложена в начале 1980-х годов Полом Бениоффом из Аргоннской национальной лаборатории, находящейся в Калифорнийском технологическом институте, и Дэвидом Дойчем из Оксфорда в Англии. Первые прототипы квантовых компьютеров не были построены до начала 1990-х годов, когда я придумал, как можно построить простейший вариант такого компьютера. Дэйв Винланд, лауреат Нобелевской премии в области физики, получил Нобелевскую премию в том числе за построение первых простых квантовых компьютеров. В 1994 году, однако, появился реальный стимул их производить, когда Питер Шор — тогда из AT&T, а теперь он в MIT — показал, что, если бы можно было построить квантовый компьютер, даже маленький, с несколькими десятками тысяч квантовых битов, он был бы в состоянии выполнить миллион операций — раз плюнуть для его классического предшественника. Если же вы заставите такой квантовый компьютер проделать этот симфонический расчет, то он смог бы расшифровать все коды, которые мы используем, чтобы секретно передавать информацию через интернет. И, как вы понимаете, после этого заявления множество людей навострили уши — не только частные лица, но и агентства, которые хотели бы узнать чужие секреты и при этом сохранить свои, конечно. Эти агентства и многие люди сказали: «О, было бы очень здорово создать квантовый компьютер».
Так, в первой половине 1990-х годов зародилась вся эта сфера квантовых вычислений, и я и мои коллеги начали строить квантовые компьютеры, все в мире — не все, конечно, но сотни людей во всем мире — также начали их создавать. Теперь у нас есть квантовые компьютеры, которые даже если не могут делить большие числа и взламывать коды, тем не менее могут делать ряд интересных вещей. Мы используем квантовые компьютеры здесь, в MIT, чтобы исследовать фундаментальные физические свойства материи, и даже пытаемся запрограммировать квантовый компьютер так, чтобы он помог нам увидеть, что происходило во Вселенной в самые первые моменты ее существования. Можно использовать квантовые компьютеры для исследования странных эффектов, которые носят такие названия, как «запутанность», когда частицы света знают друг о друге гораздо больше, чем они имеют право по классическим законам. Вы можете использовать квантовые вычисления и квантовую коммуникацию для передачи конфиденциальной информации, где надежность гарантирована законами природы. Даже если эти причины не являются достаточно вескими, чтобы проводить квантовые вычисления, существует другая мотивация: это очень увлекательно. Я сам работал над квантовыми компьютерами в течение последних 15 или 20 лет и получал огромное удовольствие, исследуя, как природа работает на самых крошечных и фундаментальных уровнях.

lenta.co