Кротовые норы и квантовая запутанность: есть связь. Связанные частицы квантовая механика

Квантовая запутанность вышла за пределы элементарных частиц

Квантовая запутанность — это ключ к квантовым компьютерам, криптографии и другим применениям квантовой механики в нашем мире. Кроме того, это одно из самых странных явлений во Вселенной, покрывающее огромные расстояния в мгновение ока и связывающее весь космос в единое целое. Долгое время ученые считали, что запутанность между двумя частицами — это достаточно редкое и непродолжительное событие, быстро проходящее из-за воздействия внешней среды. Однако математики из университета Case Western выяснили, что запутанность между частицами крупной системы — это норма.

Запутанность представляет собой одно из самых странных предсказаний, вытекающих из квантовой механики. Два объекта запутываются, если их физические свойства не определены, но связаны, и эта связь сохраняется даже если объекты разделяются большим расстоянием. Подробнее об этом мы писали ранее. Механизм такой связи не определен, но эксперименты показывают, что квантовая запутанность действительно работает. Когда две связанные частицы подвергаются влиянию окружающей среды, их взаимодействие с окружающей средой приводит к «просачиванию» запутанности во внешнюю среду, поэтому обнаружить ее становится сложно. Но она не исчезает.

Запутанность достаточно тонкое явление, но как часто она встречается в большом мире макроскопических объектов? Документы, опубликованные профессором Станиславом Сжареком и группой математиков из Case Western Reserve University проливают немного света на явление и показывают, что запутанность — вполне обычное явление в мире больших вещей.

Анализ исключительно статистический, квантовые вероятности изучаются с помощью инструментов геометрического функционального анализа. Эта сфера математики хорошо подходит для решения проблем, связанных с большим числом измерений.

Системы из нескольких частиц, как правило, находятся в состоянии, близком к чистому. В таком состоянии ни одна из внутренних частиц не связывается с другой. Частицы такой системы не выказывают никаких признаков запутанности. Вы можете создать состояние нескольких частиц, в котором они будут запутаны, но оно будет довольно необычным.

Теперь представьте большую систему, которую составляют тысячи (или триллионы частиц). Квантовое описание будет точно таким же, как и выше, но то, как меняются квантовые атрибуты в зависимости от увеличения масштабов, а тем более вероятности — все значительно усложняется и возрастает. Теперь чистое состояние будет представлять лишь небольшую часть возможных квантовых состояний, и в результате поведение частиц будет иным — и они будут запутываться.

Команда Сжарека также подсчитала возможности запутанности подсистем в системе запутанных частиц. Если вы возьмете две частицы из системы, шанс, что они запутаны, будет невелик. Даже больше: он будет крайне мало, почти нулевым, если смотреть на огромную систему. С другой стороны, если вы разделите систему на две, эти половины почти наверняка будут запутаны друг с другом.

В итоге анализ показал, что в системах, в которых имеется огромное число частиц, пара крошечных подсистем не будет запутываться друг с другом, но пара больших подсистем почти наверняка будет запутана. Если вы представите две подсистемы, в каждой из которых будет примерно одна пятая от общего числа частиц, они почти наверняка будут запутаны. Резкое изменение поведения запутанности характерно для геометрии пространств с большим количеством измерений.

Результаты показали, что повседневные объекты построены таким образом, что их части запутаны друг с другом, а также со всем, с чем взаимодействовали ранее. Этот результат достаточно интересен для тех, кто думает о Вселенной как об одном целом, но есть ли у этой целостности какие-нибудь наблюдаемые следствия? Это очень сложный вопрос, на который у нас пока нет однозначного ответа.

Крупномасштабная запутанность направляет развитие нашего мира, иногда — самым решительным образом. Тем не менее, предсказать, что может внезапно произойти, чаще всего представляется невозможным. Многие полагают, что случайность лежит в самом глубоком устройстве вселенной. Чтобы знать эти вещи наверняка, нужно слишком много знаний о микроскопическом состоянии мира. Кто-то может остроумно заявить, что и магия работает, только не проявляет реальных или предсказуемых эффектов. Что ж, в любом случае, для квантовой механики это будет справедливым суждением.

hi-news.ru

Кротовые норы и квантовая запутанность: есть связь

Физики-теоретики обнаружили связь между кротовыми норами в пространстве-времени и явлением квантовой запутанности. Возможно, их открытие — шаг на пути к одной из величайших целей теоретической физики: примирить квантовую механику с общей теорией относительности Эйнштейна.

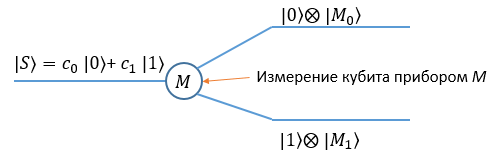
Квантовая запутанность связывает частицы таким образом, что манипуляции с одной из них могут мгновенно отразиться на другой, как бы далеко она не находилась. При этом, согласно странным законам квантового мира, каждая из частиц может находиться в одном из двух противоположных состояний — или в обоих одновременно. Так, проекция спина элементарной частицы на заданное направление может быть положительной, отрицательной, либо находиться в суперпозиции этих состояний — быть и положительной, и отрицательной одновременно, пока попытка измерить спин не приведет к коллапсу волновой функции (переходу к одному из двух направлений). Если речь идет о паре квантово запутанных частиц, измерение спина одной из них (допустим, его проекция оказалась положительной) немедленно приведет к тому, что вторая частица перейдет из суперпозиции двух возможных состояний в состояние с определенным спином (его проекция будет отрицательной). Это произойдет мгновенно, даже если частицы будут находиться во многих световых годах друг от друга.

Кротовые норы — это топологические особенности пространства-времени, описанные в рамках ОТО. Предполагается, что массивные объекты деформируют ткань пространства-времени, создавая эффект гравитации. Если масса объекта очень велика, создаваемая им «яма» в пространстве-времени будет настолько глубока, что даже свет не сможет покинуть её — образуется черная дыра. Теоретически, при соединении двух черных дыр «спина к спине» эти «ямы» могут слиться в тоннель, пронизывающий пространство-время — кротовую нору.

На первый взгляд, как явление квантовой запутанности, так и кротовые норы предлагают заманчивую возможность обойти ограничение ОТО, согласно которому ни один материальный объект не может двигаться быстрее света. Но на самом деле использовать квантовую запутанность для передачи информации быстрее скорости света нельзя, так как невозможно повлиять на то, в каком именно состоянии окажется частица-«передатчик» после проведенного измерения, а значит, невозможно и целенаправленно задать требуемое состояние частицы-«приемника». Точно также невозможно и проскользнуть сквозь кротовую нору, поскольку ничто не сможет покинуть черную дыру, расположенную на её противоположном конце.

В июне 2013 года физики-теоретики Хуан Малдасена из Института перспективных исследований в Принстоне (США) и Леонард Сасскинд из Стэнфордского университета (США), показали, что между парой квантово запутанных черных дыр формируется кротовая нора. А теперь две независимых группы ученых утверждают, что для формирования кротовой норы вовсе не нужны столь массивные объекты — она может протянуться между двумя квантово запутанными кварками.

Кристан Дженсен из Университета Виктории (Канада) и Андреас Карч из Университета Вашингтона (США), описали квантово запутанную пару, состоящую из кварка и антикварка, которые мчатся прочь друг от друга с околосветовыми скоростями, что делает невозможной передачу сигналов от одного к другому. Исследователи полагают, что трехмерное пространство, в котором движутся кварки — это гипотетическая грань четырехмерного мира. В 3D-пространстве квантово запутанные частицы соединены своего рода «струной». А в 4D-пространстве эта «струна» становится кротовой норой.

Джулиан Соннер из Массачусетского технологического института (США) представил квантово-запутанную пару кварк-антикварк, рождающуюся в сильном электрическом поле, которое разлучает противоположно заряженные частицы, заставляя их ускоренно двигаться в разных направлениях. Соннер также пришел к выводу, что частицы, квантово запутанные в трехмерном пространстве, будут соединены кротовой норой в четырехмерном.

При расчетах физики использовали так называемый голографический принцип — концепцию, согласно которой вся физика n-мерного мира в полной мере отражается на его «гранях» с количеством измерений (n-1). При таком «проецировании» квантовая теория, учитывающая эффекты гравитации в четырехмерном пространстве, эквивалентна квантовой теории «без гравитации» в трехмерном. Другими словами, черные дыры в 4D-пространстве и кротовая нора между ними математически эквивалентны их трехмерной голографической проекции. «Запутанность и кротовая нора не существуют в одном и том же пространстве, однако математически они эквивалентны», — поясняет Карч.

Сасскинд и Малдасена обращают внимание, что в обеих новых работах изначальные квантовые частицы рассматриваются в рамках моделей, не учитывающих влияние гравитации. В упрощенной, «безгравитационной» модели нашего мира не может быть никаких черных дыр и кротовых нор, поэтому связь квантовой запутанности с кротовой норой остается лишь математической аналогией. Их эквивалентность «имеет смысл только в теории с гравитацией», говорит Сасскинд. Однако Карч считает, что даже их упрощенная модель «дает вполне определенное представление о том, что кротовые норы и квантовая запутанность могут быть различными проявлениями одной и той же физической реальности».

По сообщению Science Now

www.popmech.ru

Квантовая механика

Quantum mechanics

h = 6.6.10-34 Дж.с = 4.1.10-15эВ.с). Этому условию, как правило, удовлетворяют микрочастицы. Квантовая механика включает в себя классическую механику как частный случай, реализующийся для макрообъектов. Обычно в нерелятивистской квантовой механике рассматривается движение микрочастиц, для которых скорость v << с, где с – скорость света.

Квантовая механика в основном была создана в течение первых трёх десятилетий 20-го века благодаря работам М. Планка, А. Эйнштейна, Н. Бора, А. Комптона,

Л. де Бройля, В. Паули, М. Борна, В. Гейзенберга, Э. Шрёдингера и П. Дирака.

Физической основой квантовой механики является корпускулярно-волновой дуализм, согласно которому любому материальному объекту – частице или волне – присущи как волновые, так и корпускулярные свойства. Корпускулярно-волновой дуализм наиболее ярко проявляется у микрообъектов. Его следствием является необходимость отказа от некоторых классических представлений, возникших в результате наблюдений за движением макроскопических тел. В частности волновые свойства частиц несовместимы с представлением об их движении по определённым классическим траекториям.

Волновые свойства частицы, например, электрона, требуют и соответствующего “волнового” её описания. В квантовой механике частица описывается комплексной функцией ψ(x,t), называемой волновой функцией, амплитуда которой зависит от пространственных координат х (х – совокупность координат) и времени t. Волновая функция ψ(x,t) полностью определяет состояние частицы. Как известно интенсивность любой волны определяется квадратом её амплитуды. Интенсивность волны, связанной с материальной частицей, определяется квадратом модуля волновой функции, т.е. величиной |ψ|2 = ψ*ψ. Однако, в отличие от классической волны, величина |ψ(х,t)|2 есть вероятность обнаружить частицу в момент времени t в единичном объеме вокруг точки пространства с координатами x. Этот вероятностный характер поведения частицы, во-первых, позволяет отразить волновые свойства объектов при их корпускулярном описании и, во-вторых, принципиально отличает квантовую систему от классической. В классической физике знание положения и импульса частицы в начальный момент и сил, действующих на неё, полностью и однозначно определяет её положение и импульс во все последующие моменты. Т.е. движение классических объектов полностью предопределено (детерминировано). В квантовой механике можно говорить лишь о вероятности обнаружить частицу в каком-то месте пространства, даже при полном знании её начальных кинематических характеристик и всех внешних полей, действующих на неё. И это не связано с какой-то неполнотой квантовых законов, а заложено в природе микрообъектов. Об этом свидетельствуют и соотношения неопределённостей, например, (x,t) Δx·Δp ≈ ћ (Δx – неопределённость в координате, а Δp – неопределённость в импульсе системы). Если потребовать чёткой локализации частицы в пространстве в какой-то момент, т.е. потребовать Δx ≈ 0, то в этот же момент у неё будет полностью неопределённым импульс (Δp ≈ ∞). Таким образом, в следующий момент частица может неконтролируемо переместиться куда угодно и ни о каком предопределённом (детерминированном) движении частицы не может быть и речи.

Состояния в классической и квантовой физике

Классическая физика

Квантовая физика

1. Описание состояния

(x,y,z,px,py,pz)

ψ(x,y,z)

2. Изменение состояния во времени

=∂H/∂p, = -∂H/∂t,

3. Измерения

x, y, z, px, py, pz

ΔхΔpx ~ splank.gif (65 bytes)

ΔyΔpy ~ splank.gif (65 bytes)

ΔzΔpz ~ splank.gif (65 bytes)

4. Детерминизм. Статистическая теория

Динамическое

(не статистическое) описание

|ψ(x,y,z)|2

5. Гамильтониан

H = p2/2m + U(r) op_h = 2/2m + U(r)

В квантовой механике для нахождения всего набора (спектра) возможных значений какой-либо физической величины обычно решаются дифференциальные уравнения, в которых каждой наблюдаемой физической величине (энергии, импульсу, угловому моменту, координате и так далее) сопоставляется оператор (обычно дифференциальный). Во многих случаях этот спектр является дискретным (квантованным), что принципиально отличает квантовую механику от классической.

Эволюция квантовой системы в нерелятивистском случае описывается волновой функцией, удовлетворяющей уравнению Шредингера

где ψ(х,y,z,t) - волновая функция, op_h - оператор Гамильтона (оператор полной энергии системы). В нерелятивистском случае

где m – масса частицы, op_p – оператор импульса, op_U(x,y,z) – оператор потенциальной энергии частицы. Задать закон движения частицы в квантовой механике - это значит, определить значение волновой функции в каждый момент времени в каждой точке пространства. Уравнение Шредингера играет в квантовой механике такую же роль, как и второй закон Ньютона в классической механике. Знание волновой функции квантовой системы и операторов физических величин позволяет вычислить все физические величины, характеризующие данную квантовую систему. В силу недетерминированности квантово-механических предсказаний эти вычисляемые (и наблюдаемые) физические величины носят вероятностный характер, т. е. являются статистическими средними. В результате реализации такой программы можно получить исчерпывающее квантово-механическое описание поведения частицы (системы) в изолированном состоянии или во внешних полях. Так квантово-механическая задача для атома водорода сводится к решению уравнения Шрёдингера для электрона в кулоновском поле протона, с которым он связан. Решением этой задачи является дискретный (квантованный) спектр энергетических состояний (уровней) электрона, квантовые числа, характеризующие электрон в каждом из этих состояний, и, конечно, сами волновые функции электрона в каждом состоянии. Если электрон в атоме водорода не находится в самом нижнем энергетическом состоянии, то атом неустойчив и будет претерпевать эволюцию, вызванную переходами электрона на более низкие энергетические уровни. Вероятности этих переходов также вычисляются методами квантовой механики.

Волновая функция

Волнова́я фу́нкция (функция состояния, пси-функция, амплитуда вероятности) — комплексная функция, используемая в квантовой механике для вероятностного описания состояния квантовомеханической системы. В широком смысле — то же самое, что и вектор состояния.

Вариант названия «амплитуда вероятности» связан со статистической интерпретацией волновой функции: вероятность нахождения частицы (или физической системы) в данном состоянии равна квадрату абсолютного значения амплитуды вероятности этого состояния.

Физический смысл квадрата модуля волновой функции Править

Волновая функция

\! \Psi(x_1, x_2, \ldots , x_n)

зависит от координат (или обобщённых координат) системы и формируется таким образом, чтобы квадрат её модуля

\! \left|\Psi(x_1, x_2, \ldots , x_n)\right|^2

представлял собой плотность вероятности (для дискретных спектров — просто вероятность) обнаружить систему в положении, описываемом координатами

\! x_1=x_{01}, x_2=x_{02}, \ldots , x_n=x_{0n}.

Набор координат, которые выступают в роли аргументов функции, представляет собой полный набор физических величин, которые можно измерить в системе. В квантовой механике возможно выбрать несколько полных наборов величин, поэтому волновая функция одного и того же состояния может быть записана от разных аргументов. Выбранный для записи волновой функции полный набор определяет представление волновой функции. Так, возможны координатное представление, импульсное представление, в квантовой теории поля используется вторичное квантование и представление чисел заполнения или представление Фока

Если волновая функция, например, электрона в атоме, задана в координатном представлении, то квадрат модуля волновой функции представляет собой плотность вероятности обнаружить электрон в той или иной точке пространства. Если эта же волновая функция задана в импульсном представлении, то квадрат её модуля представляет собой плотность вероятности обнаружить тот или иной импульс.

Для волновых функций справедлив принцип суперпозиции, заключающийся в том, что если система может пребывать в состояниях, описываемых волновыми функциями \! \Psi_1 и \! \Psi_2, то она может пребывать и в состоянии, описываемом волновой функцией

\! \Psi_\Sigma = c_1 \Psi_1 + c_2 \Psi_2

при любых комплексных \! c_1 и \! c_2. См. также Квантовая суперпозиция.

Матричная и векторная формулировки

Любая функция может быть представлена, как бесконечная таблица из её значений, соответствующих каждому аргументу. Если представить в таком виде волновую функцию, то она станет столбцом координат бесконечномерного вектора в Гильбертовом пространстве, то есть, матрицей.

Одна и та же волновая функция в различных представлениях — будет соответствовать выражению одного и того же вектора в разных системах координат. Остальные операции с волновыми функциями так же будут иметь аналоги на языке векторов.

Функциональная (волновая), матричная и векторная формулировки математически эквивалентны.

Философский смысл волновой функции

Волновая функция представляет собой наиболее полное возможное описание квантовомеханической системы, за исключением, быть может, матрицы плотности, предложенной Л.Д.Ландау, с помощью которой можно описывать системы систем, что невозможно при использовании волновой функции (в случае обычной системы матрица плотности есть тот же квадрат модуля волновой фукнции) скоростей всех её частиц и это описание позволяло описать всё будущее и прошлое системы, то в квантовой механике некоторые параметры описать принципиально невозможно. Согласно квантовой механике, описание системы заканчивается на уровне волновой функции (и матрицы плотности) и только на уровне волновой функции (и матрицы плотности) возможно описать будущее и прошлое системы. Более подробное описание системы, например, с точностью до указания местоположений и скоростей всех её частиц — невозможно, и значения этих параметров оказываются более или менее случайными.

Таким образом, создав квантовую механику, наука дошла до состояния, когда она смогла положить конец многовековому противопоставлению детерминизма и индетерминизма. Современная наука утверждает, в мире сочетаются детерминизм и индетерминизм, и границей между ними служит... матрица плотности или волновая функция?..

Следует понимать, что проблема, которую решает квантовая механика, — это проблема самой сути научного метода познания мира. Если представить себе бильярдный стол, закрытый непроницаемой крышкой, и единственным способом исследования вопроса, есть ли на нём бильярдные шары, предположить закатывание в стол других шаров, то мы и получаем ту самую проблему, для решения которой привлечён метод квантовой механики. Пока вброшенный шар проходит сквозь стол без изменения траектории, предсказуемо, мы можем сделать вывод о том, что на траектории шара других шаров нет. Если в результате взаимодействия шаров на столе мы получаем выкатившиеся несколько шаров с различными конечными импульсами и точками, в которых шары покинули стол, то мы можем лишь предполагать о том, каким образом происходило взаимодействие в системе. Если же лузы в бильярдном столе ограничивают возможность шаров покидать стол (энергетический барьер), то система запутывается ещё больше.

Подобный пример с бильярдом очень наглядно демонстрирует те трудности, с которыми сталкиваются исследователи, разрабатывая инструменты квантовой механики.

Смешанное состояние

Смешанное состояние (смесь состояний) — состояние квантовомеханической системы, в котором не задан максимально полный набор независимых физических величин, определяющих состояние системы, а определены лишь вероятности w_1,w_2,\ldots (\sum w_i=1) нахождения системы в различных квантовых состояниях, описываемых волновыми функциями \psi_1,\psi_2,\ldots. Таким образом, в отличие от чистого состояния, смешанное состояние не описывается одной волновой функцией, а описывается матрицей плотности.

Примерами смешанных состояний могут служить:

неполяризованный пучок частиц;

газ в термостате.

Среднее значение какой-либо физической величины A (которой соответствует оператор) в смешанном состоянии определяется следующим образом:

\bar{A}=\sum_i w_i A_i,\ \ A_i=\int \psi_i^*(x)~\hat{A}~\psi_i(x)dx

В смешанном состоянии, в отличие от суперпозиции состояний, различные квантовые состояния не интерферируют между собой, так как при определении среднего складываются не волновые функции, а средние значения.

СООТНОШЕНИЯ НЕОПРЕДЕЛЕННОСТЕЙ

СООТНОШЕНИЯ НЕОПРЕДЕЛЕННОСТЕЙ — математически формулируемый принцип квантовой теории, согласно которому запрещается существование таких состояний физической системы, в которых две динамические переменные (далее обозначаемые в общем виде А и В) имели бы вполне определенное значение, если эти переменные являются канонически сопряженными величинами. Поскольку может иметь место несколько различных пар канонически сопряженных величин, постольку можно говорить во множественном числе о соотношениях неопределенностей. Хотя соотношения неопределенностей рассматриваются в качестве принципа квантовой механики, однако его действие может быть прослежено на основе понятий классической механики. Канонически сопряженные величины представляют собою математические переменные, входящие в т. н. канонические уравнения механики (уравнения Гамильтона) и определяющие состояние механической системы в любой момент времени. В качестве канонически сопряженных переменных величин выбирают обычно обобщенные координаты q и обобщенные импульсы/”. С помощью т. н. канонических преобразований можно перейти от q тир к другим канонически сопряженным величинам Q и Р, которые могут иметь другой физический смысл.

Если две переменные А и В канонически сопряжены друг с другом в смысле гамильтонова формализма, то никакой эксперимент не может привести к одновременному точному измерению таких переменных. Неточность измерения связана при этом не с несовершенством измерительной техники, а с объективными свойствами исследуемой системы. Математически соотношения неопределенностей записываются в общем виде следующим образом: ΛΑ-ΔΒ >h. Эта запись означает, что произведение погрешностей измерения канонически сопряженных величин не может быть по порядку величины меньше постоянной Планка h. Чем точнее определено значение одной из входящих в соотношение величин, тем менее определенно значение другой величины: при попытке предельно точно определить значение одной из величин неопределенность значения другой оказывается в области бесконечных значений. Учитывая чрезвычайную малость постоянной Планка h в сравнении с макроскопическими величинами той же физической размерности, приходится делать заключение, что соотношения неопределенностей существенны лишь дри изучении явлений атомного масштаба.

Математическое выражение соотношений неопределенностей было впервые сформулировано В. Гейзенбергом в 1927 в контексте проблемы парадоксального соединения волновых и корпускулярных свойств у микрочастиц. Обсуждая с ним эту проблему, Н. Бор настойчиво искал способ рационального объединения корпускулярных и волновых свойств в объектах микромира. Размышляя о теоретико-познавательных проблемах, Бор пришел тогда к идее дополнительности — корпускулярные и волновые свойства не исключают друг друга, но находятся во взаимнодополнительном отношении. Иногда принцип дополнительности Бора представляется в качестве некоего обобщения соотношений неопределенностей. Однако первоначально Гейзенберг решительно отрицал возможность такого построения новой теории, в которой учитывались бы волновые свойства частиц. Он был тогда убежден, что можно построить новую теорию исключительно на основе идеи дискретности. Конкретное же соотношение неопределенностей между координатой и импульсом частицы было сформулировано им под влиянием Бора, который полагал необходимым найти выражение для характеристики связей между корпускулярными и волновыми свойствами микрочастиц. В соотношениях неопределенностей различные дополнительные свойства частиц своеобразно объединены в одной формуле — на основе методологического принципа был построен специальный математический аппарат.

Отличительная особенность атомных процессов заключается в их корпускулярно-волновой природе, что проявляется в экспериментах. Движение частицы связано с распространением специфической волны, а сама частица может быть обнаружена в любой точке этой волны. В результате движение микрочастицы имеет вероятностный характер. Напр., в эксперименте, где изучается явление дифракции электронов, частица определенной энергии падает на дифракционную решетку; процесс падения электрона многократно повторяется. При этом возникает характерная дифракционная картина, свидетельствующая о волновых свойствах электрона, ибо явление дифракции заключается именно в отклонении от прямолинейного движения, присущего законам геометрической оптики, которая отвлекается от волнового характера физического процесса. Сама картина дифракции электрона показывает, что в акте взаимодействия электрона с дифракционной решеткой участвуют все ее ячейки. Это означает, что невозможно предсказать траекторию движения электрона при его падении на решетку, иначе говоря, невозможно узнать, в каком направлении будет двигаться электрон. Наблюдаемое явление дифракции электронов подтверждает волновую природу микрочастиц и вместе с тем указывает на вероятностный характер их поведения. В квантовой теории состояние частицы в описанной ситуации выражается волновой функцией и не может быть представлено с точностью, характерной для классических понятий. Т. о., к микроскопическим объектам неприменимы классические понятия импульса и координаты. При описании поведения микрочастиц возникает необходимость учета их квантовых свойства, что и проявляется в соотношениях неопределенностей.

Концепции квантовой механики

Квантовая механика изучает законы поведения микрочастиц (атомов, элементарных частиц)

М.Планк (изучая тепловое движение тел, 1900г.): атомы излучающего тела отдают электромагнитную энергию порциями (квантами), причем энергия одного кванта пропорциональна частоте излучения : (Джс – постоянная Планка).

А.Эйнштейн (изучая явления фотоэффекта, 1905г): свет не только излучается, но распространяется и поглощается квантами (кванты света – фотоны, существуют только в движении).

А.Эйнштейн (1909г): свет одновременно обладает и корпускулярными (квантовыми) и волновыми (электромагнитными) свойствами. Т.е. свету присущ корпускулярно-волновой дуализм (двойственность).

Л де Бройль (1924г) сформулировал универсальный корпускулярно-волновой дуализм:

каждый микрообъект проявляет себя одновременно и как частица (имеющая импульс и энергию) и как волна (с частотой и длинй волны).

Де Бройлю удалось сформулировать соотношение, связывающее импульс квантовой частицы с длиной волны, которая ее описывает ( или ).

Экспериментальное подтверждение наличия волновых свойств микрочастиц (К.Дэвиссон, Л.Джермер, 1927г) привело к выводу о том, что это универсальное явление природы, общее свойство материи. Следовательно, волновые свойства должны быть присущи и макроскопическим телам. Однако, волновые свойства макротел (и в частности, человеческого тела) не могут быть экспериментально обнаружены. Это объясняется тем, что длина волны (обратно пропорциональная массе объекта, согласно отношению Де Бройля) при большой массе столь мала, что ее обнаружение лежит за пределами возможности экспериментальной техники.

Мысленный эксперимент «микроскоп Гейзенберга»

В классической физике, построенной на ньютоновских принципах и применяемой к объектам макромира, принимается, что процесс измерения не влияет на измеряемые свойства объекта. Однако, так ли обстоит дело в микромире, позволяет понять следующий мысленный эксперимент: чтобы точно определить положение электрона в пространстве, необходимо направить на него электромагнитную волну, «осветить» его и посмотреть в некий сверхсильный «микроскоп». Но при этом сам микрообъект (например, электрон), являющийся объектом излучения, в результате взаимодействия, с направленным на него другим микрообъектом (квантом света – фотоном), изменит свое положение в пространстве. Таким образом, сам факт замера приводит к изменению положения измеряемого объекта, и неточность измерения обуславливается самим фактом проведения измерения, а не степенью точности используемого измерительного прибора.

Этот мысленный эксперимент, отражающий тот факт, что измерение невозможно без взаимодействия, взаимодействие – без воздействия на измеряемый объект и, как следствие, искажение результатов измерения, позволил В.Гейзенбергу (1927г) сформулировать принцип неопределенности (соотношение неопределенности):

( т.к. ) здесь - неопределенность (погрешность измерения) пространственной координаты микрочастицы, (или ) – неопределенность импульса (или скорости) частицы, - масса частицы, - постоянная Планка.

Принцип неопределенностей касается и других характеристик микрочастиц. Еще одна такая взаимосвязанная пара – это энергия и время протекании квантовых процессов.

Принцип Гейзенберга играет в квантовой механике ключевую роль, хотя бы потому, что достаточно наглядно объясняет, как и почему микромир отличается от знакомого нам макромира. Принцип неопределенности говорит о том, что если бы нам удалось абсолютно точно установить местоположение квантовой частицы, о ее скорости мы бы не имели ни малейшего представления; если бы нам удалось точно зафиксировать скорость частицы, мы бы не имели понятия, где она находится.

Однако, принцип неопределенности не утверждает, что у квантовых частиц отсутствуют определенные координаты и скорости (или что эти величины абсолютно непознаваемы) – он утверждает лишь, что мы не в состоянии достоверно узнать и то и другое одновременно.

Принцип дополнительности Бора (1927г)

Соотношение неопределенностей является конкретным выражением более общего положения – принципа дополнительности Бора.

Квантовомеханический принцип дополнительности:

результаты, полученные в разных экспериментах, не могут быть связаны в единую картину, но они необходимы для исчерпывающего описания квантового объекта.

В дальнейшем Бор придал принципу дополнительности широкий философский смысл: полное понимание свойств любого объекта исследования требует дополняющих взглядов на него с разных, несовместимых между собой, точек зрения.

Статистический характер квантового описания природы.

Из-за принципа неопределенностей, описание объектов квантового микромира носит иной характер, нежели привычное описание объектов ньютоновского макромира. Вместо пространственных координат и скорости, которыми привыкли описывать механическое движение, в квантовой механике объекты описываются, так называемой, волновой функцией. Гребень «волны» соответствует максимальной вероятности нахождения частицы в пространстве в момент измерения. Движение такой волны описывается уравнением Шрёдингера, которое и говорит нам, как изменяется со временем состояние квантовой системы.

Принципиальные отличия квантовой механики от классической механики заключаются прежде всего в том, что:

- ее законы являются статистическими по своей природе

- ее предсказания имеют вероятностный характер

Резюмируем все вышесказанное:

- в классической механике можно точно вычислить значения координат и скорости объекта

- в квантовой механике можно вычислить лишь вероятность того или иного значения координат, скорости и энергии частицы в заданный момент времени

- состояние системы в классической механике задается координатами и скоростями всех материальных точек системы

- состояние объекта (или системы объектов) в квантовой механике задается волновой функцией объекта (или системы объектов)

- корпускулярные свойства света легче наблюдать, когда его длина волны достаточно мала

- волновые свойства человеческого тела затруднительно наблюдать ввиду его большой массы покоя

- если в данном квантовом состоянии физические величина Х не имеет определенного значения, это означает, что можно предсказать лишь вероятность того или иного результата измерения Х

- при взаимодействии макроскопического измерительного прибора с квантовым объектом, в процессе измерения изменяется состояние измеряемого квантового объекта.

Принцип дополнительности Бора (в узком квантовомеханическом смысле):

- результаты, полученные в разных экспериментах, не могут быть связаны в единую картину, но они необходимы для исчерпывающего описания квантового объекта

- все величины, характеризующие объект, можно разделить на такие группы, что измерение величин из одной группы делает невозможным или неточным измерение соответствующих величин из другой группы

- дополнительные физические величины всегда связаны тем или иным соотношением неопределенности

- дополнительными величинами являются: координаты и импульс; энергия и время

- при точном измерении физической величины невозможно измерить точно дополнительную ей величину (это следует из принципа неопределенности)

- принцип дополнительности отражает невозможность невозмущенных измерений (это следует из принципа неопределенности).

Принцип дополнительности Бора (в широком философском смысле):

- полное понимание свойств любого объекта исследования требует взгляда на него с разных, несовместимых, дополняющих друг друга точек зрения

- исследование реальности всегда сопровождается ее изменением, а результат исследования зависит от того как оно выполняется

- значение принципа дополнительности состоит в том, что он подчеркивает равноценность разных, в том числе несовместимых точек зрения

- однозначно, одним методом невозможно описать явление, объект или субъект – необходимо привлечь дополнительные представления

- никакое отдельное знание о предмете не может быть самодостаточным, требуется дополнение в лице других наук.

Примеры проявления принципа дополнительности (в широком смысле):

- культура как цельность ее научной и гуманитарно-художественной составляющей

- человек как цельность его биологического и социального начал

- естественнонаучная и гуманитарная культуры – это два, взаимодополняющих друг друга, способа постижения мира человека

- взаимоотношения между объектом исследования и исследователем являются одним из примеров принципа дополнительности

- биологическая и социальная сущности в человеке – это две, дополняющие друг друга, характеристики

- соотношения между хаосом и порядком в процессе самоорганизации материи являются одним из примеров действия принципа дополнительности

- анализ и синтез – два метода научного познания, которые связаны друг с другом по принципу дополнительности.

Квантово-механическое описание физических явлений микромира считается единственно верным и наиболее полно отвечающим реальности. Объекты макромира подчиняются законам другой, классической механики. Граница между макро- и микромиром размыта, а это вызывает целый ряд парадоксов и противоречий. Попытки их ликвидировать приводят к появлению других взглядов на квантовую механику и физику микромира. Видимо, наилучшим образом выразить их удалось американскому теоретику Дэвиду Джозефу Бому (1917-1992).

studfiles.net

Квантовая механика

msimagelist>

Квантовая механикаQuantum mechanics

Квантовая механика – фундаментальная физическая теория, устанавливающая способ описания и законы движения микрочастиц (молекул, атомов, атомных ядер, частиц) во внешних полях. Более формально квантовая механика – это физическая теория систем, у которых физические величины, имеющие размерность углового момента (момента количества движения) сравнимы с постоянной Планка ћ (ћ = h/2π, h = 6.6.10-34 Дж.с = 4.1.10-15эВ.с). Этому условию, как правило, удовлетворяют микрочастицы. Квантовая механика включает в себя классическую механику как частный случай, реализующийся для макрообъектов. Обычно в нерелятивистской квантовой механике рассматривается движение микрочастиц, для которых скорость v << с, где с – скорость света. Квантовая механика в основном была создана в течение первых трёх десятилетий 20-го века благодаря работам М. Планка, А. Эйнштейна, Н. Бора, А. Комптона, Л. де Бройля, В. Паули, М. Борна, В. Гейзенберга, Э. Шрёдингера и П. Дирака. Физической основой квантовой механики является корпускулярно-волновой дуализм, согласно которому любому материальному объекту – частице или волне – присущи как волновые, так и корпускулярные свойства. Корпускулярно-волновой дуализм наиболее ярко проявляется у микрообъектов. Его следствием является необходимость отказа от некоторых классических представлений, возникших в результате наблюдений за движением макроскопических тел. В частности волновые свойства частиц несовместимы с представлением об их движении по определённым классическим траекториям. Волновые свойства частицы, например, электрона, требуют и соответствующего “волнового” её описания. В квантовой механике частица описывается комплексной функцией ψ(x,t), называемой волновой функцией, амплитуда которой зависит от пространственных координат х (х – совокупность координат) и времени t. Волновая функция ψ(x,t) полностью определяет состояние частицы. Как известно интенсивность любой волны определяется квадратом её амплитуды. Интенсивность волны, связанной с материальной частицей, определяется квадратом модуля волновой функции, т.е. величиной |ψ|2 = ψ*ψ. Однако, в отличие от классической волны, величина |ψ(х,t)|2 есть вероятность обнаружить частицу в момент времени t в единичном объеме вокруг точки пространства с координатами x. Этот вероятностный характер поведения частицы, во-первых, позволяет отразить волновые свойства объектов при их корпускулярном описании и, во-вторых, принципиально отличает квантовую систему от классической. В классической физике знание положения и импульса частицы в начальный момент и сил, действующих на неё, полностью и однозначно определяет её положение и импульс во все последующие моменты. Т.е. движение классических объектов полностью предопределено (детерминировано). В квантовой механике можно говорить лишь о вероятности обнаружить частицу в каком-то месте пространства, даже при полном знании её начальных кинематических характеристик и всех внешних полей, действующих на неё. И это не связано с какой-то неполнотой квантовых законов, а заложено в природе микрообъектов. Об этом свидетельствуют и соотношения неопределённостей, например, (x,t) Δx·Δp ≈ ћ(Δx – неопределённость в координате, а Δp – неопределённость в импульсе системы). Если потребовать чёткой локализации частицы в пространстве в какой-то момент, т.е. потребовать Δx ≈ 0, то в этот же момент у неё будет полностью неопределённым импульс (Δp ≈ ∞). Таким образом, в следующий момент частица может неконтролируемо переместиться куда угодно и ни о каком предопределённом (детерминированном) движении частицы не может быть и речи.

Состояния в классической и квантовой физике

Классическая физика

Квантовая физика

1. Описание состояния

(x,y,z,px,py,pz)

ψ(x,y,z)

2. Изменение состояния во времени

=∂H/∂p, = -∂H/∂t,

3. Измерения

x, y, z, px, py, pz

ΔхΔpx ~ ΔyΔpy ~ ΔzΔpz ~

4. Детерминизм. Статистическая теория

Динамическое (не статистическое) описание

|ψ(x,y,z)|2

5. Гамильтониан

H = p2/2m + U(r)

= 2/2m + U(r)

где ψ(х,y,z,t) - волновая функция, - оператор Гамильтона (оператор полной энергии системы). В нерелятивистском случае

где m – масса частицы, – оператор импульса, (x,y,z) – оператор потенциальной энергии частицы. Задать закон движения частицы в квантовой механике - это значит, определить значение волновой функции в каждый момент времени в каждой точке пространства. Уравнение Шредингера играет в квантовой механике такую же роль, как и второй закон Ньютона в классической механике. Знание волновой функции квантовой системы и операторов физических величин позволяет вычислить все физические величины, характеризующие данную квантовую систему. В силу недетерминированности квантово-механических предсказаний эти вычисляемые (и наблюдаемые) физические величины носят вероятностный характер, т. е. являются статистическими средними. В результате реализации такой программы можно получить исчерпывающее квантово-механическое описание поведения частицы (системы) в изолированном состоянии или во внешних полях. Так квантово-механическая задача для атома водорода сводится к решению уравнения Шрёдингера для электрона в кулоновском поле протона, с которым он связан. Решением этой задачи является дискретный (квантованный) спектр энергетических состояний (уровней) электрона, квантовые числа, характеризующие электрон в каждом из этих состояний, и, конечно, сами волновые функции электрона в каждом состоянии. Если электрон в атоме водорода не находится в самом нижнем энергетическом состоянии, то атом неустойчив и будет претерпевать эволюцию, вызванную переходами электрона на более низкие энергетические уровни. Вероятности этих переходов также вычисляются методами квантовой механики.

nuclphys.sinp.msu.ru

Элементарные частицы в квантовой механике

из "Квантовая механика"

Е настоящее время известно сравнительно большое число частиц электроны, протоны, нейтроны, ц-мезоны, я-мезоны, Х-мезоны и др., которые называются сэлементарньши частицами , так как на современном этапе наших знаний нельзя говорить о структуре этих частиц. Такие частицы характеризуются определенными значениями массы покоя и могуг быть либо нейтральными, либо электрически заряженными (положигель-но и отрицательно). Абсолютная величина электрического заряда всех устойчивых заряженных частиц одинакова. [c.234] Кроме электрического заряда элементарные частицы характеризуются и другими зарядами . Так, легкие часгицы нейтрино, электроны и л-мезоны (мюоны) имеют лептонный заряд. Протоны, нейтроны и более тяжелые частицы — гипероны имеют барионный заряд. я -мезоны (пионы), А -мезоны (каоны) и другие более тяжелые мезоны не имеют лептонного и барионного зарядов. [c.234] Одной из наиболее харакгерных особенностей элементарных частиц является возможность их рождения, уничтожения и взаимных превращений в результате взаимодействий. Так, фотоны рождаются при изменении характера движения электронов в атомах или протонов в атомных ядрах. При столкновении нуклонов большой энергии рождаются пионы. Нейтрон, излучая электрон и антинейтрино, превращается в протон. С другой стороны, прогоны, входящие в состав атомных ядер, испуская нейтрино и позитрон, могут превращаться в нейтрон. Нейтральный пион превращается в два фотона заряженный пион превращается в нейтрино и мюон. Фотоны в поле ядра могуг превратиться в электрон и позитрон и т. д. [c.234] НОСТИ ОДНИХ частиц от других становится все более и более неопределенным. Согласно современным представлениям, взаимодействия между частицами одного типа передаются с помощью частиц другого типа. Так, например, заряженные и нейтральные пионы передают ядерные взаимодействия между нуклонами. Образно говоря, протоны и нейтроны как бы окружены мезои-ным облаком, через которое и осуществляется взаимодействие между ними. Это мезонное облако является составной частью протонов и нейтронов и во многом определяет их свойства. С другой стороны, протоны и нейтроны в свою очередь определяют ряд свойств пионов. В связи с этим теряет смысл понятие изолированной частицы того или иного вида. Следовательно, представление о свободном движении частицы может быть только грубой идеализацией действительности. [c.235] В явлениях, сопровождающихся взаимодействием частиц большой энергии, теряет смысл представление о неизменном числе частиц. Так, например, быстрый электрон, пролетая в поле ядра, образует фотоны, фотоны в поле ядер создают пары частиц электрон и позитрон, которые в свою очередь создают фотоны и т. д. Такое лавинообразное нарастание числа частиц наблюдается при попадании в атмосферу Земли первичных частиц из космического пространства. [c.235] Описание явлений, происходящих при больших энергиях, должно базироваться на релятивистских волновых уравнениях, т. е. на уравнениях, инвариантных относительно преобразования Лоренца. Переход от нерелятивистского описания к релятивистскому связан с необходимостью пересмотра ряда понятий нерелятивистской квантовой теории. Прежде всего требует изменения понятие координаты отдельной частицы. Нерелятивистская квантовая механика допускает возможность как угодно точной локализации частицы в пространстве и времени. В релятивистской квантовой механике одной частицы невозможна локализация частицы в пространстве, линейные размеры которого меньше Ь1 Атс), где т — масса покоящейся частицы, так как в противном случае в силу соотношения неопределенностей ( 13) частице будет сообщаться энергия р 1 2т) 2тс , которая достаточна для образования пары частиц. Таким образом, представление об одной частице можно сохранить только при отсутствии внешних воздействий, приводящих к локализации частицы в пространстве, линейные размеры которого меньше комптоновской длины волны (Ь/ тс)) соответствующей частицы. Для предельно релятивистских частиц — световых квантов (т. = О, ц = с) — понятие координаты частицы в обычном смысле полностью отсутствует. [c.235] Если имеется неопределенность в положении Ах Ь1(тс), то неизбежна и неопределенность во времени й/(тс2). [c.235] в релятивистской теории понятие плотности вероятности р х,у,г,1) положения частицы в определенный момент времени требует существенного пересмотра. В нерелятивистской теории с оо и может быть равно нулю. [c.236] Хотя представление о системах, состоящих из постоянного числа частиц, и является грубой идеализацией (в явлениях, протекающих при больших энергиях), это представление приходится использовать как первый этап в развитии более строгой теории. Такое упрощение задачи неизбежно связано с появлением ряда трудностей, обусловленных искусственным игнорированием неразрывной связи между различными частицами и их взаимной превращаемостью. [c.236] С внутренними степенями свободы элементарных частиц, такими, как спин частицы и ее зарядовая переменная. Полученные результаты будут применены к исследованию движения электрона в атоме водорода с учетом релятивистских поправок порядка и к исследованию изменений энергетических уровней атомной системы во внешнем электрическом и магнитном полях. [c.237]

Вернуться к основной статье

chem21.info

Что значит квантовая механика - Значения слов

волновая механика, теория устанавливающая способ описания и законы движения микрочастиц (элементарных частиц, атомов, молекул, атомных ядер) и их систем (например, кристаллов) а также связь величин, характеризующих частицы и системы, с физическими величинами, непосредственно измеряемыми в макроскопических опытах. Законы К. м. составляют фундамент изучения строения вещества. Они позволили выяснить строение атомов , установить природу химической связи , объяснить периодическую систему элементов , понять строение ядер атомных , изучать свойства элементарных частиц . Поскольку свойства макроскопических тел определяются движением и взаимодействием частиц, из которых они состоят, законы К. м. лежат в основе понимания большинства макроскопических явлений. К. м. позволила, например, объяснить температурную зависимость и вычислить величину теплоёмкости газов и твёрдых тел, определить строение и понять многие свойства твёрдых тел (металлов, диэлектриков, полупроводников). Только на основе К. м. удалось последовательно объяснить такие явления, как ферромагнетизм , сверхтекучесть , сверхпроводимость , понять природу таких астрофизических объектов, как белые карлики , нейтронные звёзды , выяснить механизм протекания термоядерных реакций в Солнце и звёздах. Существуют также явления (например, Джозефсона эффект ), в которых законы К. м. непосредственно проявляются в поведении макроскопических объектов. Ряд крупнейших технических достижений 20 в. основан по существу на специфических законах К. м. Так, квантово-механические законы лежат в основе работы ядерных реакторов , обусловливают возможность осуществления в земных условиях термоядерных реакций, проявляются в ряде явлений в металлах и полупроводниках, используемых в новейшей технике, и т.д. Фундамент такой бурно развивающейся области физики, как квантовая электроника , составляет квантовомеханическая теория излучения . Законы К. м. используются при целенаправленном поиске и создании новых материалов (особенно магнитных, полупроводниковых и сверхпроводящих). Т. о., К. м. становится в значительной мере «инженерной» наукой, знание которой необходимо не только физикам-исследователям, но и инженерам. Место квантовой механики среди других наук о движении. В начале 20 в. выяснилось, что классическая механика И. Ньютона имеет ограниченную область применимости и нуждается в обобщении. Во-первых, она не применима при больших скоростях движения тел ≈ скоростях, сравнимых со скоростью света. Здесь её заменила релятивистская механика, построенная на основе специальной теории относительности А. Эйнштейна (см. Относительности теория ). Релятивистская механика включает в себя Ньютонову (нерелятивистскую) механику как частный случай. Ниже термин «классическая механика» будет объединять Ньютонову и релятивистскую механику. Для классической механики в целом характерно описание частиц путём задания их положения в пространстве (координат) и скоростей и зависимости этих величин от времени. Такому описанию соответствует движение частиц по вполне определенным траекториям. Однако опыт показал, что это описание не всегда справедливо, особенно для частиц с очень малой массой (микрочастиц). В этом состоит второе ограничение применимости механики Ньютона. Более общее описание движения дает К. М., которая включает в себя как частный случай классическую механику. К. м., как и классическая, делится на нерелятивистскую, справедливую в случае малых скоростей, и релятивистскую, удовлетворяющую требованиям специальной теории относительности. В статье изложены основы нерелятивистско

xn--b1algemdcsb.xn--p1ai

Формирование квантовой механики. элементарные частицы

⇐ ПредыдущаяСтр 4 из 6Следующая ⇒

К началу XX столетия появились экспериментальные результаты, которые трудно было объяснить в рамках классических представлений. В этой связи был предложен совершенно новый подход - квантовый, основанный на дискретной концепции.

Физические величины, которые могут принимать лишь определенные дискретные значения, называются квантованными.

Квантовая механика (волновая механика) - физическая теория, устанавливающая способ описания и законы движения микрочастиц (элементарных частиц, атомов, молекул, атомных ядер) и их систем.

Существенным отличием квантовой механики от классической, является ее принципиально вероятностный характер.

Для классической механики характерно описание частиц путем задания их положения в пространстве (координат) и импульса (количества движения m.v). Такое описание не применимо для микрочастиц.

Квантовые представления впервые ввел в физику немецкий физик М Планк в 1900 г.

Он предположил, что свет испускается не непрерывно (как это следовало из классической теории излучения), а определенными дискретными порциями энергии - квантами.

В 1905 году А. Эйнштейном была выдвинута гипотеза о том, что свет не только испускается и поглощается, но и распространяется квантами.

Квант света называется фотоном. Этот термин ввел американский физико-химик Льюис в 1929 году. Фотон - частица, не имеющая массы покоя. Фотон всегда находится в движении со скоростью, равной скорости света.

Эффект Комптона. В 1922 году американский физик Комптон открыл эффект, в котором впервые во всей полноте проявились корпускулярные свойства электромагнитного излучения (в частности, света). Экспериментально было показано, что рассеяние света свободными электронами происходит по законам упругого столкновения двух частиц.

В 1913 году Н. Бор применил идею квантов к планетарной модели атома.

Гипотезу о всеобщности корпускулярно-волнового дуализма выдвинул Луи де Бройль. Элементарные частицы - это и корпускулы (частицы) и волны одновременно, а точнее — диалектическое единство свойств тех и других. Движение микрочастиц в пространстве и времени нельзя отождествлять с механическим движением макрообъекта. Движение микрочастиц подчиняется законам квантовой механики.

Окончательное формирование квантовой механики как последовательной теории связано с работой Гейзенберга 1927 года, в которой был сформулирован принцип неопределенностей, утверждающий, что любая физическая система не может находиться в состояниях, в которых координаты ее центра инерции и импульс одновременно принимают вполне определенные точные значения.

До открытия элементарных частиц и их взаимодействий наука разграничивала два вида материи - вещество и поле. Еще в конце XIX-начале XX века поле определяли как непрерывную материальную среду, а вещество - как прерывное, состоящее из дискретных частиц.

Однако развитие квантовой физики выявило относительность разграничительных линий между веществом и полем.

В современной физике поля и частицы выступают как две неразрывно связанные стороны микромира, как выражение единства корпускулярных (дискретных) и волновых (континуальных, непрерывных) свойств микрообъектов. Представления о поле выступают также как основа для объяснения процессов взаимодействия, воплощая принцип близкодействия.

Элементарные частицы, в точном значении этого термина, - это первичные, далее неразложимые частицы, из которых, по предположению, состоит вся материя. Элементарные частицы современной физики не удовлетворяют строгому определению элементарности, поскольку большинство из них по современным представлениям являются составными системами.

Первая элементарная частица - электрон был открыт Дж,Дж. Томсоном в 1897 г.

После электрона было предположено существование фотона (1900 г)– кванта света.

Далее, в 1911г., был открыт протон – положительно заряженная тяжелая элементарная частица с массой покоя – в 1840 раз больше массы е.

Затем следует открытие целого ряда других частиц: нейтрона, мезонов, гиперонов и т.д.

В 1928 г. Дирак предсказал существование частицы, имеющей ту же массу, что и электрон, но с противоположным зарядом. Эту частицу назвали позитроном. И она действительно была обнаружена в 1932 году в составе космических лучей американским физиком Андерсоном.

Современной физике известно более 400 элементарных частиц, в основном нестабильных, и их число продолжает расти.

Существуютчетыре вида основных фундаментальных физических взаимодействий:

гравитационное - характерно для всех материальных объектов вне зависимости от их природы.
электромагнитное - ответственно за связь электронов и ядер в атомах и связь атомов в молекулах.
сильное - скрепляет нуклоны (протоны и нейтроны) в ядре и кварки внутри нуклонов.,
слабое -управляет процессами радиоактивного распада частиц.

По типам взаимодействия элементарные частицы делят на

Адроны (тяжелые частицы - протоны, нейтроны, мезоны и др.) участвуют во всех взаимодействиях.
Лептоны (от греч. leptos - легкий; например, электрон, нейтрино и др.) не участвуют в сильных взаимодействиях, а только в электромагнитных, слабых и гравитационных.

При столкновениях элементарных частиц происходят всевозможные превращения их друг в друга (включая рождение многих дополнительных частиц), не запрещаемые законами сохранения.

Фундаментальные взаимодействия, преобладающие между объектами:

- микромира - (сильное, слабое и электромагнитное)

- макромира - (электромагнитное)

- мегамира - (гравитационное)

Современная физика пока еще не создала единой теории элементарных частиц, на пути к ней сделаны лишь первые, но существенные шаги.

Великое объединение – это название используется для теоретических моделей, исходящих из представлений о единой природе сильного, слабого и электромагнитного взаимодействий

открытие в ХVII в. законов механики позволило создать всю машинную технологию цивилизации;
открытие в ХIХ в. электромагнитного поля, привело к развитию электротехники, радиотехники, а затем и радиоэлектроники;
создание в ХХ в теории атомного ядра, привело к использованию ядерной энергии;

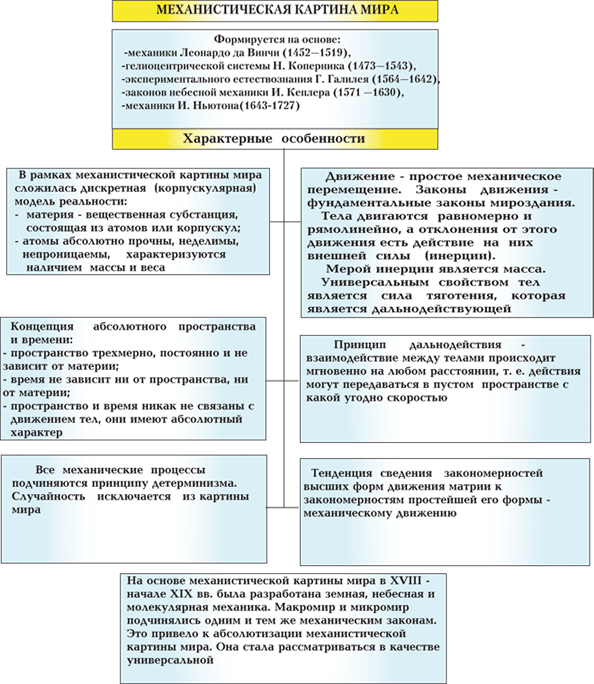
В рамках данной картины мира все События и Перемены были взаимосвязаны и взаимообусловлены механическим движением.

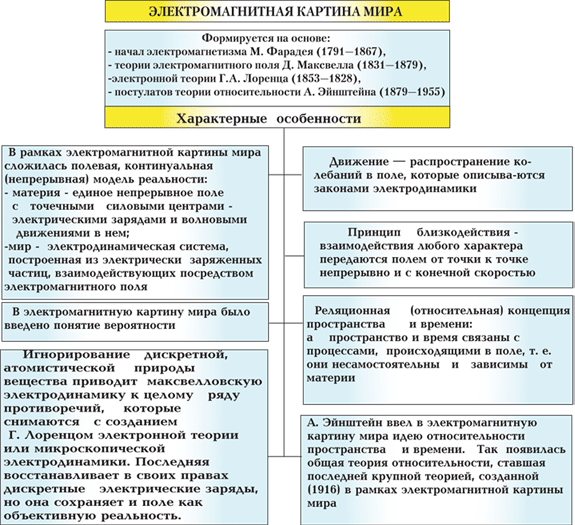
Возникновение электромагнитной картины мира характеризует качественно новый этап эволюции науки.

Сравнение данной картины мира с механистической выявляет некоторые важные особенности.

Например,

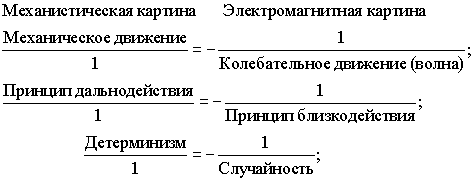
Подобная взаимодополнительность картин не является случайностью. Она носит строго эволюционный порядок.

Квантово-полевая картина мира явилась результатом дальнейшего развития электромагнитной картины мира.

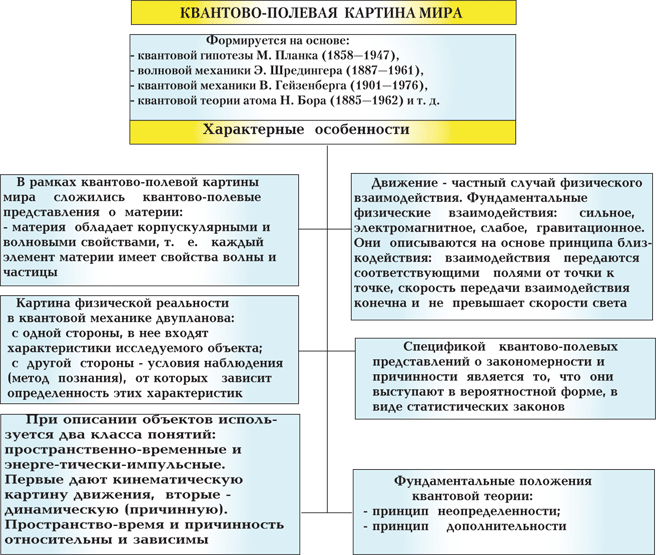
Эта картина мира отражает уже единство двух предыдущих картин мира в единстве на основе принципа дополнительности. В зависимости от постановки эксперимента микрообъект показывает либо свою корпускулярную природу, либо волновую, но не обе сразу. Эти две природы микрообъекта взаимно исключают друг друга, и в то же время должны быть рассмотрены как дополняющие друг друга.