Где встречаются большие числа: Числа-гиганты / Хабр |

Содержание

Как называются очень большие числа

В математике пятого класса она из первых тем — это позиционная система счисления. Все знают, что, например, цифра 1 может означать разное число в зависимости от того, на каком месте она стоит. Наша система счисления десятичная, поэтому разрядные единицы отличаются в 10 раз.

Если хотите узнать, при чём тут Малыш и Карлсон, сколько цифр в квадриллионе и почему европейцев поражает значение госдолга США всего-навсего в триллион долларов — читайте дальше!

Начальные разрядные единицы это:
1 — единица
10 — десять
100 — сто
1000 — тысяча

Далее идут
10 000 — десять тысяч (в Древней Греции это число называлось мириада и до Архимеда греки считали, что его достаточно, чтобы подсчитать всё на свете).
100 000 — сто тысяч
1 000 000 — миллион. (Кстати, у чисел сто и миллион есть одна интересная особенность. Подумайте, какая, а ответ вы найдёте в блоге о занимательной математике «Десять букв»)

После миллиона принцип формирования названий разрядных единиц такой.
Узловые разрядные единицы — это числа с количеством нулей, кратным трём. После каждой узловой единицы идут две, обозначающие десятки и сотни этих узловых единиц.
10 000 000 — десять миллионов
100 000 000 — сто миллионов

Дальше идёт новая узловая единиц:
1 000 000 000 — миллиард (или биллион)

Следующие за ним:
1 000 000 000 000 — триллион
1 000 000 000 000 000 — квадриллион
1 000 000 000 000 000 000 — квинтиллион
1 000 000 000 000 000 000 000 — секстиллион
1 000 000 000 000 000 000 000 000 — септиллион
1 000 000 000 000 000 000 000 000 000 — октиллион
1 000 000 000 000 000 000 000 000 000 000 — нониллион
1 000 000 000 000 000 000 000 000 000 000 000 — дециллион

В дециллионе тридцать нулей. Казалось бы, пора остановиться. Но латинский язык богат и если взять числительные «одиннадцать», «двенадцать», «тринадцать» и т.д. можно называть числа с 36-ю, 39-ю, 42-мя нулями и ещё большие.
1 000 000 000 000 000 000 000 000 000 000 000 000 — ундециллион
1 000 000 000 000 000 000 000 000 000 000 000 000 000 — дудециллион
1 000 000 000 000 000 000 000 000 000 000 000 000 000 000 — тридециллион
. …

Разумеется, говоря про большие числа, нельзя не сказать о гуголе, единице с сотней нулей. Это число больше, чем количество элементарных частиц в видимой области Вселенной. Оно дало название поисковой системе Гугл.

Теперь перейдём к ответам на поставленные в начале вопросы. Как вы помните, в мультфильме «Малыш и Карлсон» Малыш оценивал себя в сто тысяч миллионов. Неужели он не знал слова миллиард, в неполные семь-то лет? Так вот, оказывается, что в Дании используется длинная система нумерации больших чисел. И узловые «-ллионы» встречаются не через три, а через шесть нулей. Так что выражение «сто тысяч миллионов» вполне корректно математически.

Длинная система нумерации используется во всей западной Европе, кроме Великобритании, а также во франко- и испаноговорящих странах. Часто между «-ллионами» используются «-ллиарды».

Таблица соответствия названий длинных числе в короткой системе нумерации и в длинной

Короткая система — Длинная система

Миллион = Миллион

Биллион (Миллиард) = Миллиард

Триллион = Биллион

Квадриллион = Биллиард

Квинтиллион = Триллион

Секстиллион = Триллиард

Септиллион = Квадриллион

Октиллион = Квадриллиард

Нониллион = Квинтиллион

Дециллион = Дециллиард

Так что на вопрос «сколько цифр в квадриллионе» вполне можно ответить: «всё не так однозначно». В короткой системе 16, а в длинной — 25.

Ну и европецы, узнав, что долг США превысил один триллион долларов (1 000 000 000 000 в короткой системе) думают, что он составляет 1 000 000 000 000 000 000$, то есть в миллион раз больше своего фактического значения! 😀

Научно-практическая работа на тему «Большие числа и бесконечность»

Информационный
проект:

«Большие
числа и бесконечность.

Что
мы с вами знаем о бесконечности?»

Работу выполнили:

Пикалов
Максим и Коркин Егор,

ученики 11-А
класса.

Руководитель работы:

учитель
математики

МКОУ
Заволжского лицея,

Румянцева
В.С.

Заволжск 2014
год

Рецензия
на работу:

«Большие числа и бесконечность. Что
мы с вами знаем о бесконечности?»

Данный исследовательский проект содержит необходимые разделы: цель, задачи,
методы исследования, основное содержание, ожидаемые выводы и ориентацию на
информацию в интернете.

Эта работа отличается от всех других проектов своей креативностью. Проект
затрагивает весьма интересующие вопросы о бесконечности настоящего времени.

В своей работе ученики собрали информацию, которая касается бесконечности
чисел, от самых маленьких до грандиозно больших. Также Максим и Егор привели
множество разных примеров чисел, такие как Гугл, Гугл Плекс, число Грэма.
Ребята провели анкетирование учащихся школы по данной теме исследования и,
проанализировав полученные результаты, оценили их, что помогло более углубиться
в «бесконечность».

Сочетание теоретической и практической работы, способствовало творческому и
интеллектуальному развитию ребят.

Самое главное – то, что исследования проведенные учениками очень востребованы.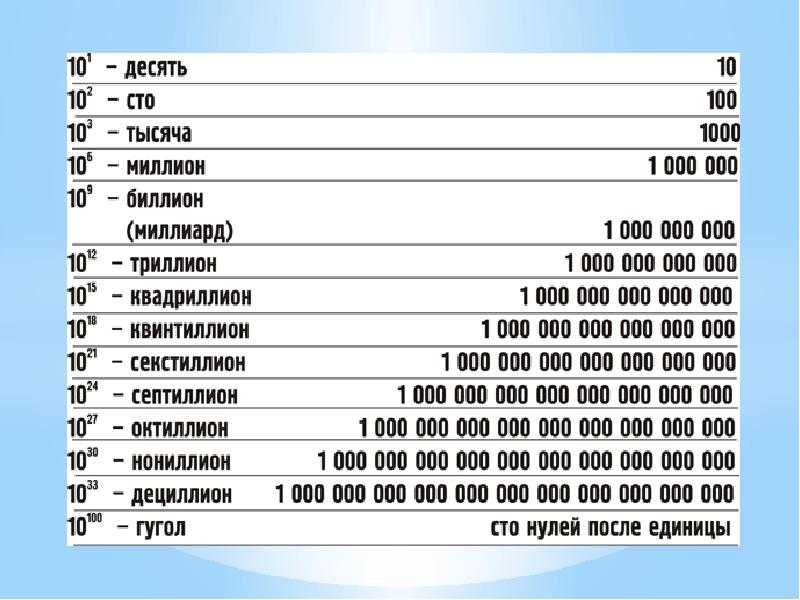
Это обусловлено тем, что множество людей задаются вопросом о бесконечности и не
могут найти на этот вопрос ответа.

«Большие
числа и бесконечность.

Что
мы с вами знаем о бесконечности?»

Гипотеза: Какое самое большое число и можно ли его вывести?

Существует
ли предел бесконечности?

Цель работы: Исследовать большие числа , оценить явление бесконечности.
Сформулировать понятие о «бесконечности» и её «пределе» . Рассмотреть
особенности этого естественного явления.

Задачи:

a.
Изучить
литературу и Интернет-данные на тему «большие числа» и «бесконечность»;

b.
Подробнее
узнать о таких числах как Гугл (Googol) и Гугл Плекс (Googolplex), про число Грэма и числа Скьюза;

c.
Провести
анкетирование учащихся школы по теме исследования.

d.
Проанализировать
полученные результаты, оценить их.

Методы:

a.
Анкетирование;

b.
Сбор
информации;

c.
Систематизация
материала в форме презентации;

Актуальность:

Миллионы
людей сейчас являются пользователями Интернета, каждый день они обращаются к
какой-то поисковой системе. Многие из них даже не подозревают, почему поисковая
система «Google» так называется.

Каждый ребенок, когда научится
считать, хотя бы до десяти задает взрослым вопрос : « А какое число самое
большое?». « Вырастешь – узнаешь»-отвечают взрослые. Этот вопрос является
важным шагом в процессе понимания мира абстрактных понятий. Ответ на этот
вопрос, как правило, ограничивается утверждением, что большие числа считаются
бесконечными. Однако в определённый момент выясняется, что числа могут быть
такими большими, что их практическое применение в реальной жизни и невозможно,
и бессмысленно, и единственное, что оправдывает их существование — это факт их
формального существования.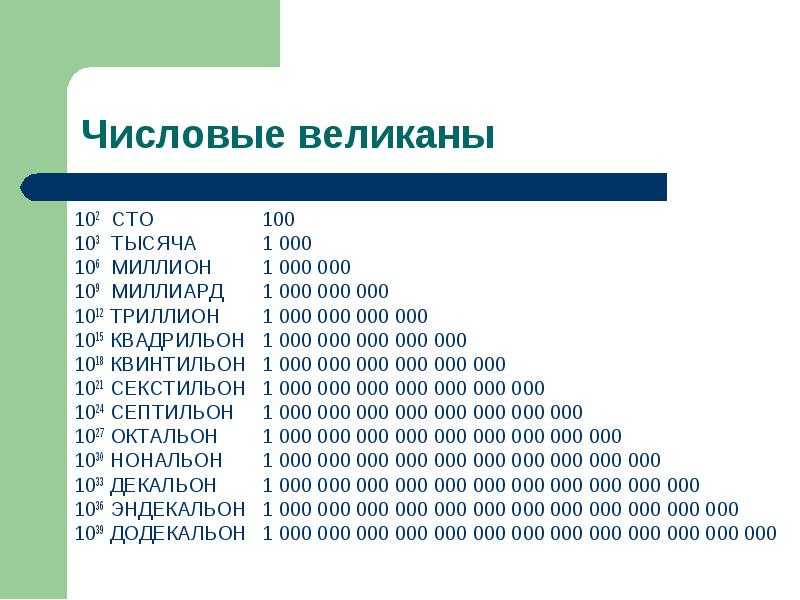

Мы выросли и решили сами разобраться с большими числами , в общем и с числом

Гугол, в частности.

Кроме этого мы решили ,образно сказать , прикоснуться к «бесконечности»

Все люди знают это число и
используют его для описания чего-то непостижимо огромного. Однако бесконечность
— не такое простое понятие, как кажется на первый взгляд.

Бесконечность — это философский
термин, свойство объекта не уменьшаться при конечном убавлении, отсутствие
границ или мер. В математике это вид отсутствия конечной числовой меры для
предела на проекции или в последовательности. В астрономии примером
бесконечности является Вселенная.

Основная часть:

Вступление:

Для того чтобы понять, что такое
«бесконечность», имеет ли она «предел», рассмотрим это явление с разных точек
зрения. В нашем случае это – математика, физика, астрономия.

Начнём наше исследование с математики.
Все мы знаем, что «бесконечностью» в этой области науки являются числа. Мы
постарались найти самое большое число в этом потоке цифр, чтобы лучше укрепить
наше мнение о этом явлении и глубже раскрыть его.

Математическое обоснование «бесконечности»:

Есть числа, которые так , невероятно
велики, что даже для того чтобы записать их, потребуется вся вселенная целиком.
Некоторые из этих непостижимо больших чисел крайне важны для понимания мира.
Есть много претендентов на этот титул.

Чтобы составить список огромных чисел, мы
могли бы просто записать какое-то огромное число под номером один, а затем
прибавлять +1, +2, +3 и так далее до конца списка. Вместо этого, мы решили
взять 7 чисел, которые имеют определенную область применения в реальной жизни. (-19) метра, что примерно в 20 тысяч раз меньше размера протона. Из
кварков состоят адроны, в частности, протон и нейтрон.

Лептон — фундаментальная частица с полуцелым
спином, собственным моментом импульса элементарных частиц, не
участвующая в сильном взаимодействии. Наряду с кварками лептоны составляют
неотъемлемую часть Стандартной модели.

Число второе

Один Гугол (Googol):

Часто используемое название популярной
поисковой системы произносится почти также, как и слово googol (гугол). Это
число имеет очень интересную историю.

Эдвард Казнер (Edward
Kasner)

В 1938 году известный американский математик Эдвард
Казнер гулял по парку с двумя своими племянниками и обсуждал с ними большие
числа. В ходе разговора зашла речь о числе со ста нулями, у которого не было
собственного названия. Один из племянников, девятилетний Милтон Сиротта,
предложил назвать это число «гугол» (googol). В 1940 году Эдвард Казнер совместно
с Джеймсом Ньюманом написал научно-популярную книгу «Математика и воображение»
(«New Names in Mathematics»), где и рассказал любителям математики о числе
гугол.

Алексис Лемар (Alexis
Lemaire)

Это относительно абстрактное и формально
существующее число, которому нашлось применение в определённых областях. К
примеру: «Человек-Калькулятор» (Alexis Lemaire) установил мировой рекорд,
вычислив корень 13-й степени из 100-значного числа (для сравнения: корень 13-й
степени из числа 8,192 равняется 2). Стозначное число – это гугол. Одно из
чисел, которые Лемар вычислял, произносилось следующим образом – 3 гугола 893
дуотригинтиллиона (3 googol, 893 duotrigintillion)…и так далее. Еще одна
область применения данного числа — это обозначение промежутка времени, примерно
от 1 до 1.5 гугола лет, которые пройдут со времени большого взрыва, до взрыва
самой массивной черной дыры.

Число третье

«8.5 х 10185»:

Планковская длина или постоянная Планка
равняется примерно 1.616199 x 10−35 метров, или, если записать это в более
длинном варианте — 0.00000000000000000000000000000616199 метра. В одном
кубическом дюйме насчитывается около одного гугола планковских длин.
Планковская длина играет важную роль в теории струн (область квантовой физики),
и из-за своей малой длины теоретически позволяет определить неизвестные ранее
измерения.

Почему такие ничтожно малые значения
оказались в этом списке? Во вселенной насчитывается примерно 8. 5 х 10185
планковских длин. Это огромное число и практического применения не имеет,
однако это число довольно легко сравнивать с остальными числами в списке.

Число
четвертое

«243.112.609-1»:

Предыдущее 185-значное число равнялось
количеству планковских длин во вселенной. Под номером 4 идет 13.000.000–значное
число. Формальное существование этого числа заключается в том, что оно является
самым большим простым числом. Число было открыто в 2008 с помощью проекта по
распределённому поиску простых чисел Мерсенна (GIMPS). Начиная со следующего
номера в списке, числа будут намного сложнее для понимания.

Число пятое

Гуголплекс (Googolplex):

Многие люди слышали это число в жизни.
Поклонники фильма «Назад в Будущее» помнят, как Доктор Эмит бормотал себе под
нос – «она одна на миллион, на миллиард, на гуголплекс…»

Что же это за число – гуголплекс?
Помните чему равен гугол? Гугол – это число со ста нулями после единицы. 100.

10 — десять

100 — сто

1 000 — тысяча

1 000 000 — миллион

1 000 000 000 — миллиард

1 000 000 000 000 — триллион

1 000 000 000 000 000 — квадрильон

1 000 000 000 000 000 000 — квинтильон

1 000 000 000 000 000 000 000 — секстильон

1 000 000 000 000 000 000 000 000 — септильон

1 000 000 000 000 000 000 000 000 000 — октальон

1 000 000 000 000 000 000 000 000 000 000
— нональон

1 000 000 000 000 000 000 000 000 000 000 000
— декальон

1 000 000 000 000 000 000 000 000 000 000 000
000 — эндекальон

1 000 000 000 000 000 000 000 000 000 000 000
000 000 — додекальон

И… число гигант:

10 000 000 000 000 000 000 000 000 000 000 000
000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000
000 000 — ГУГОЛ

Число шестое

Числа Скьюза:

Это верхний предел математической
проблемы, выраженной простым, на первый взгляд, уравнением: π(x) > Li (x). 963.

Число седьмое

Число Грэма:

Число Грэма (Грехема, англ. Graham’s
number) — большое число, которое является верхним пределом для решения
определённой проблемы в теории Рамсея. В 1980 году Число Грэма было занесено в
книгу Рекордов Гиннесса, как самое большое конечное число, которое
использовалось в серьезных математических расчетах. Это число настолько
огромное, что даже степенные башни, практически не в состоянии отобразить его.
Единственный способ, который позволит отобразить Число Грэма – это стрелочная
нота́ция Кнута и специальные стрелочные операторы Кнута. Давайте разберем все
по порядку.

Во-первых, стрелочная нотация Кнута это
метод записи очень больших чисел. Здесь будет довольно сложно вкратце
объяснить, как работают стрелочные операторы Кнýта. Однако вы можете
представить их в таком виде: 3↑3 обозначает число 27, а 3↑↑3 означает число 327
(7,625,597,484,987). Если добавить еще одну стрелку, 3↑↑↑3, то мы получим
степенную башню с 7500000000000 уровнями. Это число намного больше, чем время
возвращения Пуанкаре, а вы можете добавлять еще стрелки, и получать еще более
огромные числа.

Число Грэма (G) выражается следующей
формулой: G=f64 (4), где f (n)=3↑n3. Рассмотрим это число по уровням. Первый
уровень – это 3↑↑↑↑3, число настолько большое, что его очень затруднительно
отобразить в какой-либо другой форме. Следующий уровень имеет несколько стрелок
между тройками. Добавляя стрелки между тройками, мы можем дойти до 64 уровня.
Если вам интересно, то последние цифры Числа Грэма -2464195387, а вот про
первые цифры Числа Грэма не знает никто, даже сам Грэм.

Итог анализа математических чисел:

Проанализировав эти огромные числа, мы
пришли к мнению, что предел чисел не возможен. Его просто не существует. Однако не все уверены,
что предел чисел бесконечен. Израильский математик, профессор Дорон Зельбергер
(Doron Zeilberger), убежден, что числа не могут увеличиваться бесконечно, и
существует такое огромное число, что если вы прибавите к нему единицу, вы
получите ноль. Тем не менее, это число и его значение лежат далеко за пределами
человеческого понимания, и вероятно, это число никогда не будет найдено и
доказано. Это убеждение является главным принципом математической философии,
известной как «Ультрабесконечность».

К бесконечности

Так есть
числа больше, чем число Грэма? Есть, конечно, для начала есть число Грэма .

дальше

Интересные математические свойства
бесконечности:

Согласно правилам бесконечности, существует
бесконечное число, как четных, так и нечетных чисел. Тем не менее, нечетных
чисел будет ровно половина от общего количества чисел. Бесконечность плюс
единица равняется бесконечность, если отнять единицу получаем бесконечность,
сложив две бесконечности получим бесконечность, а бесконечность поделённая на
два равняется бесконечности, а если вычесть бесконечность из бесконечности, то
результат не вполне ясен, а вот бесконечность поделённая на бесконечность,
скорее всего, равняется единице.

Астрономическое обоснование «бесконечности»:

В этой области науки «бесконечность»
выступает в роли Вселенной. Вселенная в астрономии такая же бесконечная, как и
числовой поток в математике.

Ученые определили, что в известной нам
части Вселенной существует 1080 субатомных частиц, это та часть, которую ученые
исследовали. Многие ученые уверены, что Вселенная бесконечная, а ученые,
которые скептически относятся к бесконечности Вселенной, в данном вопросе
всё-таки допускают такую вероятность.

Если Вселенная бесконечна, то с математической
точки зрения получается, что где-то находится точная копия нашей планеты,
поскольку существует вероятность, что атомы «двойника» занимают такое же самое
положение, как и на нашей планете. Шансы, что такой вариант существует,
ничтожно малы, хотя, в бесконечной Вселенной, это не только возможно, но и
обязательно должно произойти, и, по меньшей мере, бесконечное число раз, при
условии, что Вселенная все-таки бесконечно бесконечна.

Анкетирование учащихся школы по теме
исследования:

Мы провели опрос на тему «бесконечности» в
нашей школе. Задавали учащимся следующие вопросы:

· Какое самое большое число вы знаете?

· Как вы думаете, существует ли предел
бесконечности?

· Верите ли вы в то, что во Вселенной существует
такая же планета как и наша Земля, основываясь на бесконечное пространство?

После анкетирования мы составили схемы ответов
учеников МКОУ Заволжского лицея :

Подведём итоги:

Явление «бесконечности»
весьма трудно понять и изучить полностью. Если основываться на числа, то Изучение чисел и их свойств необходимо каждому современному
человеку для развития логического мышления, памяти, творческого решения задач.
В школьном курсе «математика» не изучается тема «числа — великаны», но узнав,
что существуют числа больше миллиарда,мы решили больше узнать об этих числах.
Безусловно, мало знать, как называются самые большие числа в мире, имеющие
собственное название. Интересно было узнать и посмотреть на то, как они
записываются, где встречаются в жизни.

Проделанная исследовательская
работа помогла больше узнать о больших числах, какие ученые занимались их изучением.В
ходе работы мы расширили свой кругозор в области математики.Мы были удивлены,
что числа великаны и названия их появились давно. Оказывается, они окружают нас
повсюду. Подробно изучив мы можем рассказать о них нашим одноклассникам на
уроке. Полученные знания помогут нам в дальнейшем в изучении предметов физика,
химия, математика.

Приложения

Значок бесконечности в реальной жизни

А) в природе

Б) в быту

Во Вселенной)

‎Познакомьтесь с цифрами в App Store

Описание

Это игра Preschool Prep Company для iPhone: встречайте числа! С числовыми символами из отмеченного наградами DVD «Встреча с числами» ваш малыш может проверить свои знания о числах, выбирая их, как они называются!

На экране черным шрифтом отображаются три числа. Рассказчик называет число, и когда ваш ребенок нажимает на правильное число, он превращается в персонажа отмеченного наградами DVD: Meet the Numbers. Большие числа облегчают нажатие маленьким пальчикам, а веселая праздничная музыка в каждой сцене побуждает их играть снова и снова!

ОСОБЕННОСТИ
— Цифры от 0 до 10
— Достаточно просто для вашего малыша
— БОЛЬШИЕ числа для маленьких пальчиков
— Сцена со счетом в конце каждой игры
— Веселое празднование после каждого правильного ответа

BE ОБЯЗАТЕЛЬНО ПОПРОБУЙТЕ ДРУГИЕ ИГРЫ КОМПАНИИ ДЛЯ ДОШКОЛЬНОЙ ПОДГОТОВКИ В APP STORE! А также другие продукты компании Preschool Prep Company по адресу: www.preschoolprepco.com

*Были известные проблемы совместимости с iOS версии 7 или более ранней, пожалуйста, обновите программное обеспечение вашего устройства через iTunes, если у вас возникли проблемы с этим или любым другим нашим продуктом. Программы.

000Z» aria-label=»May 22, 2019″> 22 мая 2019 г.

Версия 5.0

— С числами от 0 до 10
— Достаточно просто для вашего малыша
— БОЛЬШИЕ числа для маленьких пальчиков
— Сцена счета в конце каждой игры
— Весёлый праздник после каждого правильного ответа

Рейтинги и обзоры

4 оценки

Требуется несколько исправлений

Это отличное приложение, но оно требует нескольких исправлений:
1) громкость возвращается к максимальному значению после каждого раунда. Он должен оставаться установленным после того, как вы опустите его.
2) снимите кнопку «Назад» после начала воспроизведения. Мой сын, у которого есть особые потребности, всегда попадает в нее случайно.
3) разрешить только два номера
Спасибо!

Нашему 18-месячному ребенку нравятся эти приложения

Она радостно визжит, когда мы даем ей телефон с приложением для подготовки к школе. Мои единственные жалобы — это пустые паузы между тем, как она получает правильный предмет, и ликующими персонажами, а также случайные сбои / зависания игры. Всякий раз, когда он выходит из строя (что чаще всего случается с номерами), она с обеспокоенным выражением лица возвращает мне мой телефон. Тем не менее, мы с нетерпением ждем приложений Sight Word.

Слишком легко вернуться в меню

Слишком легко вернуться в меню. Мой сын постоянно возвращается в меню, из-за чего две сцены накладываются друг на друга.

Разработчик Preschool Prep Company не предоставил Apple подробностей о своей политике конфиденциальности и обработке данных. Для получения дополнительной информации см. политику конфиденциальности разработчика.

Подробности не предоставлены

Разработчик должен будет предоставить сведения о конфиденциальности при отправке следующего обновления приложения.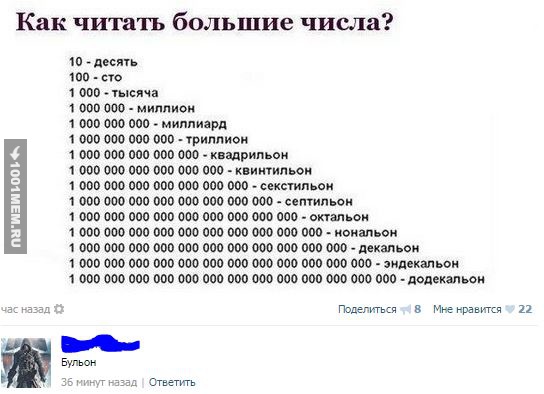

Информация

Продавец: Компания дошкольной подготовки
Размер: 72 МБ
Категория: Игры
Возрастной рейтинг: 4+
Цена: 0,99 $

Сайт разработчика
Тех. поддержка
Политика конфиденциальности

Опоры

Еще от этого разработчика

«Страна больших чисел», Те-Пин Чен: NPR

Обзор: «Страна больших чисел», Те-Пин Чен сборник рассказов о китайской жизни, которые заставят читателей пересмотреть свои устоявшиеся представления.

Рассмотрение

Отзывы о книге

6 февраля 2020 г., 17:00 по восточноевропейскому времени.

Камил Ахсан

Маринер

Mariner

Когда опытные журналисты обращаются к беллетристике, я часто думаю: «Ах, вот и беда». Мы не обращаем на это достаточного внимания, но у журналистов действительно есть преимущество, возможность выявлять писателей, не пользуясь обширными репортажами. В конце концов, художественная литература — как учат нас уроки ремесла — требует повышенной наблюдательности. Это классно трудный урок.

Страна больших чисел , дебютный сборник рассказов Тэ-Пина Чена — репортера Wall Street Journal и бывшего корреспондента Journal в Пекине и Гонконге — является блестящим примером острый глаз журналиста, проявляющийся в яркой фантастике, которую только можно найти. Более десяти историй, действие которых происходит в основном в Китае, Чен демонстрирует способность с удивительной легкостью переходить от отдельных людей к сообществам, от оседлого среднего класса до сельской бедноты, от ярых диссидентов до сторонников Коммунистической партии Китая (КПК).

Интервью с авторами

«Страна больших чисел», сборник рассказов Те-Пина Чена

Проблема часто с художественной литературой, которая пытается сделать это, заключается в том, что читателю легко уловить то, что кажется неорганичным или менее обжитым и полностью наблюдаемым. Однако у Чена, похоже, нет проблем с преодолением классовых, гендерных и идеологических различий. Что еще может объяснить эту маловероятную книгу, переворачивающую страницы, кроме ее и без того завистливой карьеры встроенного журналиста, освещающего все, от китайской системы уголовного правосудия до технологических компаний.

Люди в центре историй часто являются комиками, несмотря на то, как по-разному Чен использует их в отношении политики. В «Летающей машине» мы встречаемся с Цао Цао, деревенским изобретателем причудливых машин, который год за годом претендует на членство в партии — всегда напрасно:

Каждый раз секретарь деревенской партии Цзян, ондатра человек в черной ветровке, любезно, но твердо отвергла его… [Партия] хотела мозгов, хотела таланта, хотела (это подразумевалось, но не говорилось) богатства.

Цао Цао делает робота из обрезков, робота, который может нарезать лапшу. Деревня собирается, и секретарь партии хвалит удивительного робота, нарезающего тесто на полоски, которые затем готовит и подает жена Цао Цао Эннинг. Но вскоре люди теряют интерес к роботу-лапше, и Цао Цао снова отказывают в членстве в партии. Десять лет спустя он начинает строить самолет. История удобно выглядит в этом комическом стиле — жителей деревни в основном забавляет эксцентричность Цао Цао — но его всепоглощающая потребность заискивать перед партией, чтобы наконец присоединиться к ней, является очевидным стремлением. Вряд ли это подтекст. Это просто так. Это поиск социальной мобильности в неизвестной деревне где-то в Китае.

Есть что-то общее в том, как Чэнь изображает Коммунистическую партию Китая с разных точек зрения: как режим, который должен быть гораздо более знаком посторонним, чем он есть на самом деле. В основном это происходит с изрядной долей равнодушия к вопросу о том, что ее (предположительно) американские читатели думают о партии в первую очередь. Это невозможный, неразрешимый вопрос, на который невозможно ответить — мы не можем знать, насколько осведомлены эти читатели о КПК и ее истории.

Есть что-то общее в том, как Чэнь изображает Коммунистическую партию Китая с разных точек зрения: как режим, который должен быть гораздо более знаком посторонним, чем он есть на самом деле.

Возможно, они знают достаточно, чтобы понять первую историю «Лулу». Лулу — близнец, ослепительно умная девушка, которая оставляет своего брата, рассказчика, в пыли, поскольку она без особых усилий зарабатывает место в столичном университете («автобус, поезд и самолет»). Но пока ее нет, ее брат замечает ее в социальных сетях, осуждающей насилие со стороны полиции, государство и внесудебные казни. Посты Лулу становятся вирусными. Он беспокоится; Яростная активистская жилка Лулу опасна. При первом аресте она отбывает шесть суток. Второй раз, три года. Ее работа — хоть и косая — не утихает. Пока жизнь ее семьи продолжается, Лулу остается в этом промежуточном пространстве неизбежного заключения; история заканчивается десятилетним приговором. Я закончил читать и остался недоволен. В конце концов, это было неполным.

Но чем еще может закончиться такая история? Ожидал ли я, как читатель, более мрачной истории? Ожидал ли я, что меня отправят в ГУЛАГ? Почему я ожидал большей жестокости? Что, если банальность концовки фактическая ? Интересно, это, возможно, большой гамбит Чена? Она изображает этот Китай так близко, что читатель может усомниться в своих устоявшихся представлениях о нем. Разве действие «Лулу» не могло происходить в Соединенных Штатах? Конечно, мог. В конце концов, большинство американцев, похоже, только сейчас осознают, сколько черных активистов прошлого и настоящего — так же, как и давно находящиеся в заключении «Черные пантеры» — были сметены системой уголовного правосудия. Преступления Лулу косвенны в том смысле, что нельзя точно указать на их малость или крупность, но общие черты очевидны: это цена крамолы , где бы ты ни был.

Заглавный рассказ так же хорошо, как и любой другой, говорит о близости современного Китая к западной или американской культуре. Представитель среднего класса Чжу-Фэн все еще живет дома. Он беспокоится: «Какая девушка когда-либо захочет выйти за него замуж, с его шутками о зарплате, без машины, без перспективы на собственное жилье?» Он получает подсказку об инвестиционной возможности в компании под названием Shandong Abundant Sanitation Ltd., и с небольшой помощью друга Чжу-Фэн входит в дивный новый мир фондовой биржи. История в книге, выпущенной на этой неделе, жутко напоминает сагу GameStop. Чванство, чванство, получай деньги… Чванство, чванство, делай ставку », — напевает Чжу-Фэн про себя. затем идет еще дальше: грандиозное зрелище обещаний и богатства с примесью фантасмагории в стиле Мира Дикого Запада . Короткая сцена показывает разгон протеста фермеров, сразу же благоухающий современной Индией. «Большие числа» специфические и острые, но в то же время поддающиеся обобщению». Эти истории могут появиться в качестве новостей прямо сейчас, в любой момент9.0009

И это самое удивительное в том, что пишет Чен. Практически все, что касается Страна больших чисел , является конкретным и захватывающим, но каким-то образом поддающимся обобщению. Эти истории могут появиться как новости прямо сейчас, в любой момент. Они могут быть подробно описаны в подробностях, даже некоторые из магических обходных путей реализма, которые делает Чен, например, история о изменяющем жизнь, умопомрачительном новом фрукте. На самом деле все это может произойти где угодно — может быть, прямо там, где вы находитесь.