Содержание
Наблюдение за Международной космической станцией (МКС)
Если выйти из дома ясной безлунной ночью за городом, то по мере того как глаза привыкнут к темноте, небо окажется буквально усыпанным звездами. И вдруг Вы замечаете неспешно перемещающуюся «звездочку». Поздравляю, Вы увидели спутник! Обычно на это не требуется более 15 минут времени.
По данным Union of Concerned Scientists на 1 сентября 2013 года в космосе находится 1084 действующих спутника, из них 530 низкоорбитальных (LEO — Low Earth Orbit Satellites) на высотах 500 — 1500 км, совершающих около 18 оборотов за сутки, 79 средневысотных (MEO или ICO — Medium Earth Orbit или Intermediate Circular Orbit Satellites), 38 — на эллиптической орбите (HEO — High Elliptic Orbit Satellites) и 437 — геостационарных (GEO — Geostationary Earth Orbit Satellites) на высоте около 36000 км.
Типы орбит спутников Земли (Computational Physics, Inc., 2014)
Одним из самых привлекательных объектов такого рода для наблюдений является Международная Космическая Станция (МКС, International Space Station, ISS).
МКС (ISS) (Википедия)
МКС состоит из нескольких модулей: американских, российских, японских и европейских. Первая секция МКС была выведена на орбиту 20 ноября 1998 года. Международную космическую станцию предполагается использовать до 2020 года с возможным продлением до 2028 года.
Орбита МКС проходит на высоте около 370 км (200 миль) над поверхностью Земли и наклонена на 51° к экватору.
Точные параметры ее орбиты:
минимальная высота над поверхностью Земли – 412,155 километра;
максимальная высота над поверхностью Земли – 439,300 километра;
период обращения – 92,824 минуты;
наклонение – 51,668 градуса.
Размеры станции таковы, что ее можно наблюдать невооружённым глазом с поверхности Земли как очень яркую «звездочку» (от 0m до -4m звездной величины ), перемещающуюся по небу с запада на восток (угловая скорость около 1 градуса в секунду).
Обычно звездная величина МКС отрицательная, что делает ее одним из самых ярких объектов на небе.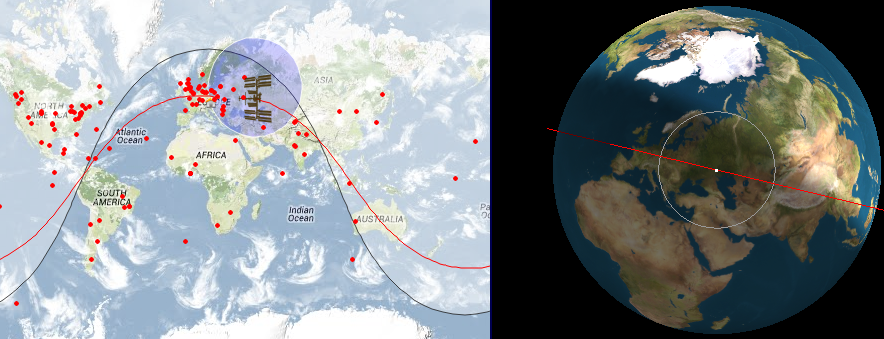
Звездные величины планет (в максимуме) и звезд:
Венера -4,67m
Юпитер -2,94m
Марс -2,91m
Ригель +0,12m
Бетельгейзе +0,50m
На сайте http://www.heavens-above.com Вы можете узнать расписание пролетов МКС над Вашим городом.
Не при каждом проходе (pass) станция видна (она может находиться в тени) — для отображения только видимых проходов надо поставить галочку «only visible«
Также такую информацию можно получить на сайте НАСА http://spotthestation.nasa.gov/sightings/index.cfm — после указания своей страны и города будет отображена таблица с информацией о видимости станции (время местное).
Также можно наблюдать перемещение Международной космической станции над Землей в реальном времени на сайте http://www.lizard-tail.com/isana/tracking/ :
Схема наблюдения МКС (http://nerdsville.blogspot.com/2012/03/well-ive-finally-seen-iss.html):
МКС видна в том случае, если ее проход в Вашей местности происходит либо вскоре после заката, либо незадолго перед восходом. Если проход случается в середине дня, то она не видна из-за яркого неба. А если он происходит около полуночи, то станция не видна, так как находится в тени Земли.
Если проход случается в середине дня, то она не видна из-за яркого неба. А если он происходит около полуночи, то станция не видна, так как находится в тени Земли.
Наиболее интересен момент наибольшей высоты станции над поверхностью Земли (в примере ниже это момент выхода из тени на высоте 29°):
ISS Event Exits shadow — выход из тени
Drops below altitude 10° — перемещение ниже высоты 10°
Sets — заход
Фотография сделана Mark Humpage
С помощью оптических приборов можно получить вот такое изображение станции:
ОАО «НПК «СПП»
Также представляет большой интерес прохождение станции по диску Солнца:
Шаттл «Атлантис» и МКС, 16.05.2010 (фотограф — Thierry Legault)
Французский астроном-любитель сфотографировал в сентябре 2009 года тень от Международной космической станции на поверхности Луны:
Фотография сделана Jérôme Delpau
Наблюдению МКС посвящена тема на Астрофоруме — http://www. astronomy.ru/forum/index.php/topic,4757.0.html .
astronomy.ru/forum/index.php/topic,4757.0.html .
МОИ НАБЛЮДЕНИЯ
Для съемки я использую цифровой фотоаппарат Casio Exilim EX-S10. У него широкая апертура (f/2.8), что вполне достаточно для съемок звезд.
Чем меньше значение диафрагмы (например, 2.8), тем больше отверстие, которое пропускает световой поток (больше светосила). Но при уменьшении размера диафрагмы уменьшается глубина резкости. Максимальная чувствительность 1600 ISO, что не так уж и плохо. Чем выше число ISO, тем более чувствительна камера.
Наблюдение 19 октября 2013 года
Пролет МКС удалось наблюдать вечером 19 октября. Погода была безоблачная, небо чистое. Сначала станция была видна как не слишком яркая звездочка, перемещающаяся совсем медленно. Но затем она становилась все ярче и ярче и перемещалась быстрее.
Параметры прохода станции:
Максимальная высота 80 градусов, станция была почти в зените.
Проход станции можно наблюдать и в астрономической программе Stellarium:
Я проводил видео- и фотосъемку прохода Международной космической станции. Так как чувствительность была выставлена на 1600 ISO и скорость перемещения станции была довольно высока, то фотографии получились такими:
Видео доступно и на моем канале на YouTube: http://youtu.be/0nuQq3Fp74s
Наблюдение 25 мая 2017 года
Яркость: — 3,9.
Начало видимости: время — 23:39:39, высота — 10°, азимут — ЗЮЗ;
наибольшая высота: время — 23:42:55, высота — 67°, азимут Ю;
конец видимости: время — 23:46:12, высота — 10°, азимут — В.
«Чем руководствовались, когда выбирали высоту орбиты МКС? Почему не немного ниже или немного выше?» — Яндекс Кью
Популярное
Сообщества
КосмонавтикаКосмос+2
Виктория Наумова
256Z»>27 февраля ·
5,6 K
ОтветитьУточнить
Достоверно
Денис Прудник
Космонавтика
269
Участник отбора в космонавты. Аспирант МАИ. Основатель проекта «Мы верим в космос».
Лауре… · 16 мар · мыверимвкосмос.рф
Высота полета МКС обусловлена:
- Стоимостью доставки грузов — чем ниже, тем дешевле. Плюс, космические корабли имеют ограничение по высоте полета и некоторые из них банально выше не долетят;
- Влияние атмосферы — чем ниже, тем сильнее МКС тормозится об атмосферу. В результате больше затрат на поддержание орбиты;
- Чем выше, тем большая радиация будет воздействовать на космонавтов. На 400км радиация не такая губительная, как на высоте от 600км, например
Сегодня орбита МКС меняется в диапазоне (грубо) от 403 до 440 км. С учетом вышеуказанных фактов это наиболее целесообразно.
Участник отбора в космонавты. Популяризатор космонавтики 🚀
Перейти на t.me/ocosmose
3 эксперта согласны
Sergei Merchenko
18 марта
Под первым пунктом, видимо, нужно было назвать радиационную опасность, разве нет? Поскольку астро/космонавты… Читать дальше
Комментировать ответ…Комментировать…
Виктор Моор
557
Увлечений нет, должности нет, род деятельности неизвестен · 27 февр
В Вики написано:
МКС рассчитана на работу на орбитах с высотой от 270 до 500 км. Это диктуется несколькими причинами:
Нижняя граница орбиты: Торможение об атмосферу
Чем ниже высота орбиты, тем больше торможение об атмосферу и тем чаще необходимо проводить коррекцию повышения орбиты. Это требует дополнительных затрат топлива. По этому фактору высоту орбиты стараются… Читать далее
1 эксперт согласен
Евгений Прокопьев
подтверждает
25 марта
Совершенно верно, только ограничения кораблей на первом месте
Комментировать ответ…Комментировать…
Почетный академик Галактической Академии Информациологии. · 9 мар
· 9 мар
По высоте над поверхностью Земли уже ответили правильно. А вот по высоте географической широты не ответили. Максимальная широта МКС соответствует Владивостоку и району южнее Волгограда. Поэтому исследование поверхности России со станции МКС неэффективно. В связи с этим чем руководствовалось наше правительство участвуя в МКС непонятно. Конечно есть другие работы на МКС… Читать далее
Комментировать ответ…Комментировать…
Mikhail Grishkov
52
Природа, лыжи, рыбалка, охота.
· 6 мар
Немного ниже или немного выше станция опускается за счет сопротивления атмосферы и за счет двигателей, которые ее поднимают. Это происходит постоянно. Высота орбиты выбирается исходя из соображений плотности атмосферы и высоты радиационных поясов на широтах полета станции, которые зависят от наклонения орбиты. Если летать внутри радиационного пояса, то космонавты и… Читать далее
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
Understanding Friction — AP Physics B
Все ресурсы AP Physics B
65 практических тестов
Вопрос дня
Карточки
Learn by Concept
AP Physics B Справка »
Ньютоновская механика »
Силы »
Понимание трения
Ящик стоит на шершавом полу с коэффициентом статического трения .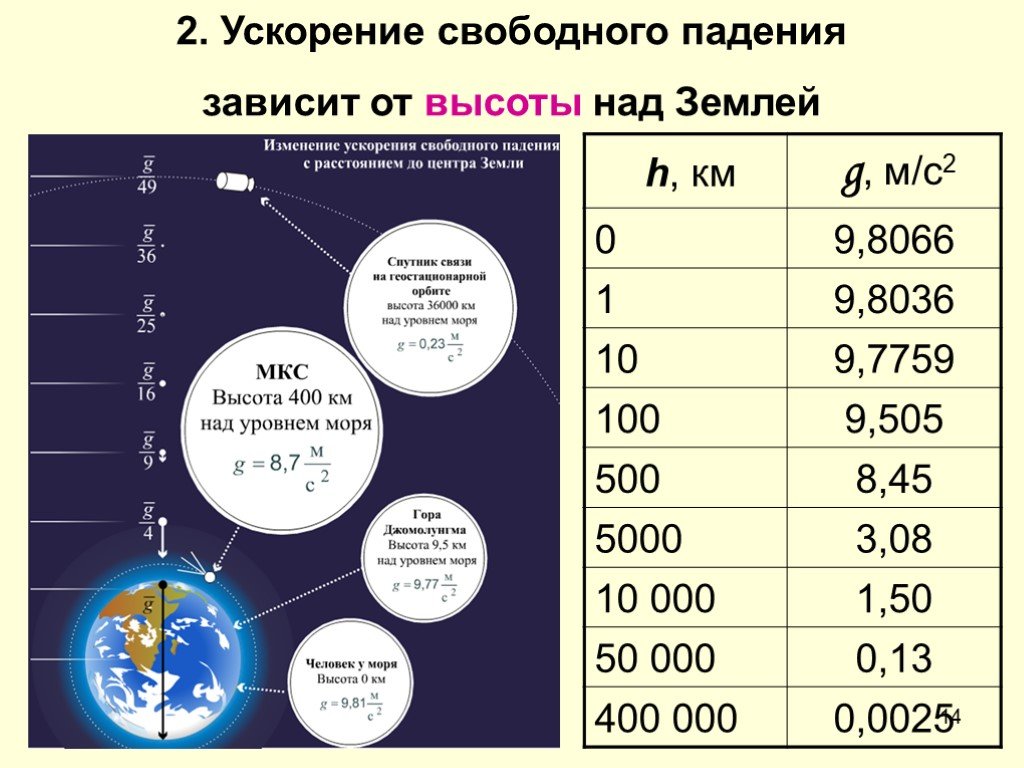 Мужчина пытается толкнуть ящик горизонтально. Какую силу должен приложить человек к ящику, чтобы сдвинуть ящик с места?
Мужчина пытается толкнуть ящик горизонтально. Какую силу должен приложить человек к ящику, чтобы сдвинуть ящик с места?
Возможные ответы:
Правильный ответ:
Пояснение:
Мы знаем, что нормальная сила, действующая на плоскую поверхность, равна и противоположна силе тяжести.
Затем найдите силу трения между ящиком и полом, используя уравнение:
Эта сила является минимальной силой, необходимой для начала движения ящика.
Сообщить об ошибке
Коробка изначально находится в состоянии покоя на горизонтальном полу с коэффициентом статического трения . К ящику приложена горизонтальная толкающая сила. Какова максимальная сила толкания, которую можно приложить, не сдвигая ящик?
Возможные ответы:
Правильный ответ:
Пояснение:
Максимальная сила, которую можно приложить, будет равна максимальному значению силы трения покоя.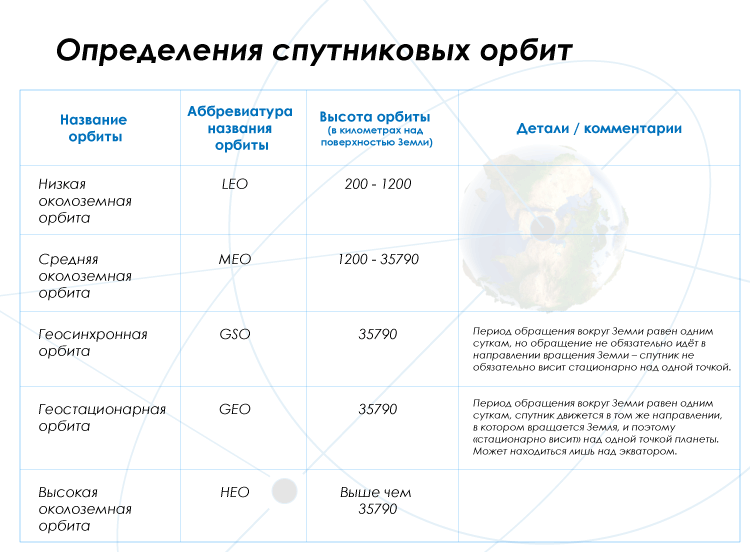 Формула трения:
Формула трения:
Мы также знаем, что нормальная сила равна и противоположна силе тяжести.
Подставляя в исходное уравнение, мы можем переписать силу трения.
Используя заданные значения коэффициента трения и массы, мы можем вычислить силу, использующую ускорение свободного падения.
Сообщить об ошибке
Человек тянет ящик вверх по склону, чтобы отдохнуть на высоте . Он выполняет в общей сложности работы. Чему равен коэффициент трения на склоне?
Возможные ответы:
Нам нужно знать массу коробки, чтобы решить
Правильный ответ:
0012
Пояснение:
Работа равна изменению энергии системы. Нам задан вес ящика и вертикальное перемещение, что позволит вычислить изменение потенциальной энергии. Это и будет полная работа, необходимая для перемещения ящика против силы тяжести.
Оставшаяся работа, которую совершает человек, должна была быть использована для противодействия силе трения, действующей против его движения.
Теперь мы знаем работу, совершаемую трением. Используя это значение, мы можем найти силу трения и коэффициент трения. Во-первых, нам нужно будет использовать вторую формулу для работы:
В этом случае расстоянием будет расстояние, пройденное по поверхности склона. Мы можем найти это расстояние с помощью тригонометрии.
Мы знаем работу трения и расстояние, пройденное по склону, что позволяет нам найти силу трения.
Наконец, используйте формулу для силы трения, чтобы найти коэффициент трения. Имейте в виду, что сила, действующая на коробку под действием силы тяжести, будет равна .
Подставьте наши окончательные значения и найдите коэффициент трения.
Сообщить об ошибке
Ящик загружается в пикап, и грузовик уезжает без соскальзывания ящика.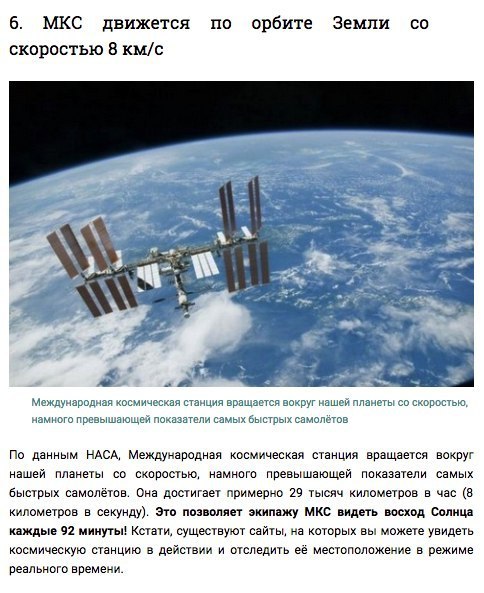 Если коэффициент трения покоя между грузовиком и ящиком равен , то какое максимальное ускорение может совершить грузовик без проскальзывания ящика?
Если коэффициент трения покоя между грузовиком и ящиком равен , то какое максимальное ускорение может совершить грузовик без проскальзывания ящика?
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы ящик не скользил, грузовик должен оказывать на него силу трения. Сила трения связана с нормальной силой коэффициентом трения.
Эта сила трения возникает из-за ускорения грузовика, основанного на втором законе Ньютона.
Две силы будут равны, когда грузовик движется с максимальным ускорением, а ящик не движется.
Решите для ускорения.
Сообщить об ошибке
Коробка весом 2 кг находится наверху пандуса под углом 60 o . Верх рампы находится на высоте 30 м над землей. Ящик неподвижно стоит наверху рампы, а затем его отпускают.
Представьте, что результирующая сила, действующая на коробку, составляет 16,5 Н при скольжении по пандусу. Чему равен коэффициент кинетического трения коробки?
Возможные ответы:
Кинетический коэффициент трения нельзя определить во время движения ящика
Правильный ответ:
5
45
4
Объяснение:
Поскольку коробка движется, когда определена результирующая сила, действующая на коробку, мы можем вычислить коэффициент кинетического трения для коробки. Первым шагом является определение чистой силы, действующей на коробку в отсутствие трения. Чистая сила, действующая на коробку, определяется уравнением .
Разница между чистой силой без трения и чистой силой с трением составляет 0,8 Н. Это означает, что сила кинетического трения на ящике равна 0,8 Н, действующая против направления движения.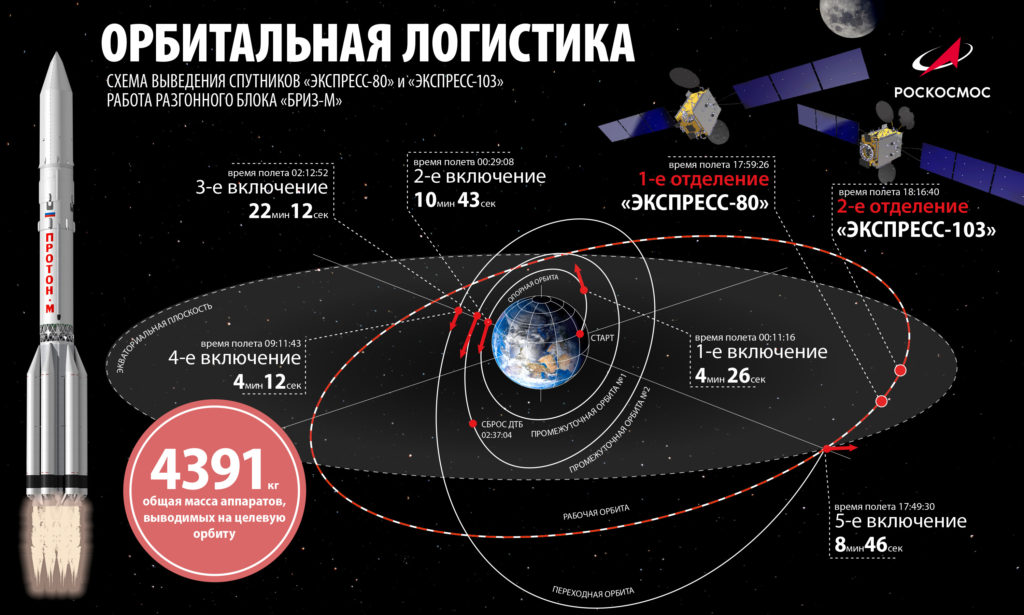 Зная это, мы можем найти коэффициент кинетического трения, используя уравнение
Зная это, мы можем найти коэффициент кинетического трения, используя уравнение
Сообщить об ошибке
Вопрос дня
Карточки
Учитесь по концепции
11.1 Перекатывание | University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Описывать физику качения без проскальзывания
- Объясните, как линейные переменные связаны с угловыми переменными для случая качения без проскальзывания
- Найти линейное и угловое ускорения при качении с проскальзыванием и без него
- Расчет статической силы трения, связанной с качением без проскальзывания
- Использование функции сохранения энергии для анализа качения
Вращательное движение — это обычное сочетание вращательного и поступательного движения, которое мы видим повсюду, каждый день. Подумайте о различных ситуациях, когда колеса движутся по шоссе, или колеса самолета приземляются на взлетно-посадочной полосе, или колеса робота-исследователя на другой планете. Понимание сил и крутящих моментов, участвующих в качении , является решающим фактором во многих различных ситуациях.
Понимание сил и крутящих моментов, участвующих в качении , является решающим фактором во многих различных ситуациях.
Для анализа качения в этой главе обратитесь к (Рисунок) в разделе Вращение с фиксированной осью, чтобы найти моменты инерции некоторых общих геометрических объектов. Вы также можете найти его полезным в других расчетах, связанных с вращением.
Перекатывание без проскальзывания
Люди наблюдали перекатывание без проскальзывания с момента изобретения колеса. Например, мы можем посмотреть на взаимодействие шин автомобиля и поверхности дороги. Если водитель нажимает педаль акселератора в пол так, что шины крутятся, а автомобиль не движется вперед, между колесами и поверхностью дороги должно быть кинетическое трение. Если водитель медленно нажимает на педаль акселератора, заставляя автомобиль двигаться вперед, то шины катятся без проскальзывания. Для большинства людей удивительно, что на самом деле нижняя часть колеса находится в покое по отношению к земле, что указывает на наличие статического трения между шинами и поверхностью дороги. На (рисунке) велосипед движется, а всадник остается в вертикальном положении. Шины соприкасаются с дорожным покрытием, и, несмотря на то, что они катятся, нижняя часть шин слегка деформируется, не скользит и находится в состоянии покоя относительно дорожного покрытия в течение измеримого промежутка времени. Для этого между шиной и поверхностью дороги должно быть статическое трение.
На (рисунке) велосипед движется, а всадник остается в вертикальном положении. Шины соприкасаются с дорожным покрытием, и, несмотря на то, что они катятся, нижняя часть шин слегка деформируется, не скользит и находится в состоянии покоя относительно дорожного покрытия в течение измеримого промежутка времени. Для этого между шиной и поверхностью дороги должно быть статическое трение.
Рисунок 11.2 (а) Велосипед движется вперед, и его шины не скользят. Нижняя часть слегка деформированной шины находится в покое относительно поверхности дороги в течение измеримого периода времени. (b) На этом изображении видно, что верхняя часть катящегося колеса кажется размытой из-за его движения, но нижняя часть колеса мгновенно остается в покое. (кредит a: модификация работы Нельсона Лоуренсо; кредит b: модификация работы Колина Роуза)
Чтобы проанализировать качение без проскальзывания, мы сначала выводим линейные переменные скорости и ускорения центра масс колеса через угловые переменные, описывающие движение колеса. Ситуация показана на (рис.).
Ситуация показана на (рис.).
Рисунок 11.3 (a) Колесо тянется по горизонтальной поверхности под действием силы [латекс] \overset{\to }{F} [/латекс]. Сила статического трения [латекс] {\overset{\to }{f}}_{\text{S}},|{\overset{\to }{f}}_{\text{S}}|\ le {\mu }_{\text{S}}N [/latex] достаточно большой, чтобы не скользить. (b) Векторы линейной скорости и ускорения центра масс и соответствующие выражения для [латекс] \omega \,\text{и}\,\alpha [/латекс]. Точка P покоится относительно поверхности. (c) Относительно системы центра масс (ЦМ) точка P имеет линейную скорость [латекс] \текст{−}R\omega \hat{i} [/латекс].
Из (Рисунок)(а) мы видим векторы сил, участвующих в предотвращении проскальзывания колеса. На (b) точка P , касающаяся поверхности, покоится относительно поверхности. Относительно центра масс точка P имеет скорость [латекс] \text{−}R\omega \hat{i} [/latex], где R — радиус колеса, а [латекс] \omega [/latex] — угловая скорость колеса относительно своей оси. Поскольку колесо катится, скорость P относительно поверхности равна его скорости относительно центра масс плюс скорость центра масс относительно поверхности:
Поскольку колесо катится, скорость P относительно поверхности равна его скорости относительно центра масс плюс скорость центра масс относительно поверхности:
[латекс] {\ overset {\ to} {v}} _ {P} = \ text {−} R \ omega \ hat {i} + {v} _ {\ text {CM}} \ hat {i }. [/latex]
Так как скорость P относительно поверхности равна нулю, [латекс] {v}_{P}=0 [/латекс], это говорит о том, что
[латекс] {v}_{ \text{CM}}=R\omega . [/latex]
Таким образом, скорость центра масс колеса равна его радиусу, умноженному на угловую скорость относительно его оси. Покажем соответствие линейной переменной в левой части уравнения угловой переменной в правой части уравнения. Это сделано ниже для линейного ускорения.
Если продифференцировать (рисунок) в левой части уравнения, то получим выражение для линейного ускорения центра масс. В правой части уравнения R является константой, и поскольку [латекс] \альфа =\фрак{д\омега} {dt}, [/латекс] мы имеем
[латекс] {а}_{\ текст{CM}}=R\alpha . [/latex]
[/latex]
Кроме того, мы можем найти расстояние, которое проходит колесо, в терминах угловых переменных, обратившись к (Рисунок). Когда колесо катится от точки A в точку B , его внешняя поверхность отображается на землю ровно на пройденное расстояние, которое составляет [латекс] {d} _ {\ text {CM}}. [/latex] Мы видим из (Рисунок), что длина внешней поверхности, которая отображается на землю, равна длине дуги [латекс] R\theta \text{} [/латекс]. Приравнивая два расстояния, получаем
[латекс] {d}_{\text{CM}}=R\theta . [/latex]
Рисунок 11.4 Когда колесо катится по поверхности, длина дуги [латекс] R\theta [/латекс] от А до В отображается на поверхность, что соответствует расстоянию [латекс] {d} _{\text{CM}} [/latex], что центр масс сместился.
Пример
Катится по наклонной плоскости
Твердый цилиндр катится по наклонной плоскости без проскальзывания, начиная с состояния покоя. Он имеет массу m и радиус r . а) Чему равно его ускорение? б) Какому условию должен удовлетворять коэффициент трения покоя [латекс] {\му }_{\текст{S}} [/латекс], чтобы цилиндр не скользил?
а) Чему равно его ускорение? б) Какому условию должен удовлетворять коэффициент трения покоя [латекс] {\му }_{\текст{S}} [/латекс], чтобы цилиндр не скользил?
Стратегия
Нарисуйте эскиз и диаграмму свободного тела и выберите систему координат. Ставим x в направлении вниз по плоскости и y вверх перпендикулярно плоскости. Определить задействованные силы. Это нормальная сила, сила тяжести и сила трения. Запишите законы Ньютона в направлениях x и y и закон Ньютона для вращения, а затем определите ускорение и силу трения.
Решение
- Диаграмма свободного тела и эскиз показаны на (Рисунок), включая нормальную силу, компоненты веса и силу трения покоя. Трения едва хватает, чтобы цилиндр вращался без проскальзывания. Поскольку проскальзывание отсутствует, величина силы трения меньше или равна [латекс] {\ mu }_{S}N [/латекс]. Запись законов Ньютона в x – и y — направления, имеем
[латекс] \сумма {F}_{x}=m{a}_{x};\enspace\sum {F}_{y}=m{a}_{y}.
 [/латекс]
[/латекс]Рисунок 11.5 Твердый цилиндр катится по наклонной плоскости, не соскальзывая с места. Система координат имеет x в направлении вниз по наклонной плоскости и y перпендикулярно плоскости. Диаграмма свободного тела показана с нормальной силой, статической силой трения и компонентами веса [латекс] m\overset{\to }{g} [/latex]. Трение заставляет цилиндр катиться по плоскости, а не скользить.
Замена из диаграммы свободного тела,
[латекс] \begin{array}{ccc}\hfill mg\,\text{sin}\,\theta -{f}_{\text{S}}& =\hfill & m{({a}_ {\ text {CM}})} _ {x}, \ hfill \\ \ hfill N-mg \, \ text {cos} \, \ theta & = \ hfill & 0, \ hfill \\ \ hfill {f} _{\text{S}}& \le \hfill & {\mu }_{\text{S}}N,\hfill \end{массив} [/latex]
мы можем тогда найти линейное ускорение центра масс из этих уравнений:
[латекс] {({a} _ {\ text {CM}})} _ {x} = g (\ text {sin} \, \ theta — {\ mu } _ {S} \ text {cos} \ ,\тета). [/латекс]
Однако полезно выразить линейное ускорение через момент инерции.
 Для этого запишем второй закон Ньютона для вращения
Для этого запишем второй закон Ньютона для вращения[латекс] \sum {\tau}_{\text{CM}}={I}_{\text{CM}}\alpha . [/латекс]
Крутящие моменты рассчитываются относительно оси, проходящей через центр масс цилиндра. Единственный ненулевой крутящий момент обеспечивается силой трения. У нас есть
[латекс] {f}_{\text{S}}r={I}_{\text{CM}}\alpha . [/латекс]
Наконец, линейное ускорение связано с угловым ускорением на
[латекс] {({a}_{\text{CM}})}_{x}=r\alpha . [/латекс]
Эти уравнения можно использовать для решения для [латекса] {a}_{\text{CM}},\alpha ,\,\text{and}\,{f}_{\text{S}} [/latex ] с точки зрения момента инерции, где мы опустили индекс x -. Запишем [латекс] {а}_{\текст{СМ}} [/латекс] через вертикальную составляющую силы тяжести и силы трения и сделаем следующие замены.
[латекс] {a}_{\text{CM}}=g\text{sin}\,\theta -\frac{{f}_{\text{S}}}{m} [/latex] 9{2})}=\frac{1}{3}\text{tan}\,\theta . [/латекс]
Значение
- Линейное ускорение линейно пропорционально [латекс] \text{sin}\,\theta .
 [/latex] Таким образом, чем больше угол наклона, тем больше линейное ускорение, как и следовало ожидать. Угловое ускорение, однако, линейно пропорционально [латекс] \текст{sin}\,\тета [/латекс] и обратно пропорционально радиусу цилиндра. Таким образом, чем больше радиус, тем меньше угловое ускорение.
[/latex] Таким образом, чем больше угол наклона, тем больше линейное ускорение, как и следовало ожидать. Угловое ускорение, однако, линейно пропорционально [латекс] \текст{sin}\,\тета [/латекс] и обратно пропорционально радиусу цилиндра. Таким образом, чем больше радиус, тем меньше угловое ускорение. - Чтобы не происходило проскальзывания, коэффициент статического трения должен быть больше или равен [латекс] (1\текст{/}3)\текст{тан}\,\тета [/латекс]. Таким образом, чем больше угол наклона, тем больше должен быть коэффициент трения покоя, чтобы цилиндр не проскальзывал.
Проверьте свое понимание
Полый цилиндр находится на наклонной поверхности под углом [латекс] 60\text{°}. [/latex] Коэффициент статического трения на поверхности [латекс] {\mu }_{S}=0,6 [/латекс]. а) Катится ли цилиндр без проскальзывания? (b) Будет ли сплошной цилиндр катиться без проскальзывания 9{2})}. [/latex]
Это очень полезное уравнение для решения задач, связанных с качением без проскальзывания. Обратите внимание, что ускорение меньше, чем у объекта, скользящего по плоскости без трения без вращения. Ускорение также будет разным для двух вращающихся цилиндров с разной инерцией вращения.
Обратите внимание, что ускорение меньше, чем у объекта, скользящего по плоскости без трения без вращения. Ускорение также будет разным для двух вращающихся цилиндров с разной инерцией вращения.
Качение с проскальзыванием
В случае качения с проскальзыванием мы должны использовать коэффициент кинетического трения, который приводит к кинетической силе трения, поскольку статического трения нет. Ситуация показана на (рис.). В случае проскальзывания [латекс] {v}_{\text{CM}}-R\omega \ne 0 [/латекс], поскольку точка P на колесе не покоится на поверхности, а [латекс] {v}_{P}\ne 0 [/латекс]. Таким образом, [латекс] \omega \ne \frac{{v}_{\text{CM}}}{R},\alpha \ne \frac{{a}_{\text{CM}}}{R} [/латекс].
Рисунок 11.6 (a) Между колесом и поверхностью возникает кинетическое трение, поскольку колесо проскальзывает. (b) Простые отношения между линейными и угловыми переменными больше не действуют.
Пример
Скатывание по наклонной плоскости с проскальзыванием
Твердый цилиндр скатывается по наклонной плоскости из состояния покоя и испытывает скольжение ((Рисунок)). Он имеет массу m и радиус r . а) Чему равно его линейное ускорение? б) Чему равно его угловое ускорение относительно оси, проходящей через центр масс?
Он имеет массу m и радиус r . а) Чему равно его линейное ускорение? б) Чему равно его угловое ускорение относительно оси, проходящей через центр масс?
Стратегия
Нарисуйте эскиз и диаграмму свободного тела, показывающую действующие силы. Диаграмма свободного тела аналогична случаю отсутствия проскальзывания, за исключением того, что сила трения является кинетической, а не статической. Используя второй закон Ньютона, найдите ускорение в x — направление. Используйте второй закон вращения Ньютона, чтобы найти угловое ускорение.
Решение
Рис. 11.7 Твердый цилиндр скатывается по наклонной плоскости из состояния покоя и испытывает скольжение. Система координат имеет x в направлении вниз по наклонной плоскости и y вверх перпендикулярно плоскости. Диаграмма свободного тела показывает нормальную силу, кинетическую силу трения и компоненты веса [латекс] m\overset{\to}g}. [/latex]
Сумма сил в y -направление равно нулю, поэтому сила трения теперь равна [латекс] {f} _ {\ text {k}} = {\ mu } _ {\ text {k}} N = {\ mu } _ {\ текст{k}}мг\текст{cos}\,\тета . [/latex]
[/latex]
Второй закон Ньютона в направлении x становится
[латекс] \sum {F}_{x}=m{a}_{x}, [/latex]
[латекс] мг \, \ текст {грех} \, \ тета — {\ му} _ {\ текст {к}} мг \, \ текст {соз} \, \ тета = м {({а} _ {\ текст {CM }})}_{x}, [/latex]
или
[латекс] {({a}_{\text{CM}})}_{x}=g(\text{sin}\, \ тета — {\ му } _ {\ текст {K}} \, \ текст {cos} \, \ тета). [/латекс] 9{2}\альфа . [/latex]
Решая для [латекс] \альфа [/латекс], мы имеем
[латекс] \альфа =\фрак{2{е}_{\текст{к}}}{мр}=\фракция {2{\mu} _{\text{k}}g\,\text{cos}\,\theta}{r}. [/latex]
Значение
Запишем линейное и угловое ускорения через коэффициент кинетического трения. Линейное ускорение такое же, как у тела, скользящего по наклонной плоскости с кинетическим трением. Угловое ускорение относительно оси вращения линейно пропорционально нормальной силе, зависящей от косинуса угла наклона. Как [латекс]\тета\до 90\text{°} [/latex], эта сила стремится к нулю, и, таким образом, к нулю обращается угловое ускорение. {2}+mgh. [/латекс]
{2}+mgh. [/латекс]
В отсутствие каких-либо неконсервативных сил, которые отбирали бы энергию из системы в виде тепла, полная энергия катящегося объекта без проскальзывания сохраняется и постоянна на протяжении всего движения. Примерами, когда энергия не сохраняется, являются катящийся объект, который скользит, выделение тепла в результате кинетического трения и катящийся объект, встречающий сопротивление воздуха.
Вы можете спросить, почему катящийся объект, который не скользит, сохраняет энергию, ведь сила трения покоя не является консервативной. Ответ можно найти, вернувшись к (Рисунок). Пункт P при контакте с поверхностью находится в состоянии покоя относительно поверхности. Следовательно, его бесконечно малое смещение [латекс] d\overset{\to }{r} [/латекс] относительно поверхности равно нулю, а дополнительная работа силы трения покоя равна нулю. Мы можем применить закон сохранения энергии к нашему изучению качения, чтобы получить некоторые интересные результаты.
Пример
Марсоход Curiosity
Марсоход Curiosity , показанный на (Рисунок), был отправлен на Марс 6 августа 2012 года. Колеса марсохода имеют радиус 25 см. Предположим, астронавты прибывают на Марс в 2050 году и обнаруживают ныне недействующий Curiosity на краю бассейна. Пока разбирают марсоход, космонавт случайно теряет сцепление с одним из колес, которое катится, не соскальзывая, на дно котловины на 25 метров ниже. Если колесо имеет массу 5 кг, какова его скорость на дне чаши?
Рис. 11.8 Марсоход Curiosity из научной лаборатории НАСА во время испытаний 3 июня 2011 года. Местонахождение находится внутри Цеха сборки космических кораблей в Лаборатории реактивного движения НАСА в Пасадене, Калифорния. (кредит: NASA/JPL-Caltech)
Стратегия
Мы используем сохранение механической энергии для анализа проблемы. На вершине холма колесо покоится и обладает только потенциальной энергией. На дне бассейна колесо имеет вращательную и поступательную кинетическую энергию, которая должна быть равна начальной потенциальной энергии по закону сохранения энергии. Поскольку колесо катится без проскальзывания, мы используем соотношение [латекс] {v}_{\text{CM}}=r\omega [/латекс], чтобы связать поступательные переменные с вращательными переменными в уравнении сохранения энергии. Затем находим скорость. Из (рис.) видно, что полый цилиндр является хорошим приближением для колеса, поэтому мы можем использовать этот момент инерции для упрощения расчета. 9{2})25,0\,\text{m}}=9,63\,\text{m}\text{/}\text{s}\text{.} [/latex]
Поскольку колесо катится без проскальзывания, мы используем соотношение [латекс] {v}_{\text{CM}}=r\omega [/латекс], чтобы связать поступательные переменные с вращательными переменными в уравнении сохранения энергии. Затем находим скорость. Из (рис.) видно, что полый цилиндр является хорошим приближением для колеса, поэтому мы можем использовать этот момент инерции для упрощения расчета. 9{2})25,0\,\text{m}}=9,63\,\text{m}\text{/}\text{s}\text{.} [/latex]
Значение
Это довольно точный результат, учитывая, что на Марсе очень мало атмосферы, и потери энергии из-за сопротивления воздуха будут минимальными. Результат также предполагает, что местность гладкая, так что колесо не будет натыкаться на камни и неровности на своем пути.
Кроме того, в этом примере кинетическая энергия или энергия движения поровну распределяется между линейным и вращательным движением. Если мы посмотрим на моменты инерции на (рисунок), то увидим, что полый цилиндр имеет наибольший момент инерции для данного радиуса и массы. Если бы колеса вездехода были твердыми и аппроксимировались твердыми цилиндрами, например, кинетическая энергия была бы больше при прямолинейном движении, чем при вращательном. Это дало бы колесу большую линейную скорость, чем приближение полого цилиндра. Таким образом, сплошной цилиндр достигнет дна бассейна быстрее, чем полый цилиндр.
Если бы колеса вездехода были твердыми и аппроксимировались твердыми цилиндрами, например, кинетическая энергия была бы больше при прямолинейном движении, чем при вращательном. Это дало бы колесу большую линейную скорость, чем приближение полого цилиндра. Таким образом, сплошной цилиндр достигнет дна бассейна быстрее, чем полый цилиндр.
Резюме
- При качении без проскальзывания между катящимся объектом и поверхностью возникает сила трения покоя. Соотношения [латекс] {v}_{\text{CM}}=R\omega ,{a}_{\text{CM}}=R\alpha ,\,\text{and}\,{d}_ Применяются все {\text{CM}}=R\theta [/latex], так что линейная скорость, ускорение и расстояние до центра масс представляют собой угловые переменные, умноженные на радиус объекта.
- При качении с проскальзыванием между катящимся объектом и поверхностью возникает кинетическая сила трения. В этом случае [латекс] {v}_{\text{CM}}\ne R\omega ,{a}_{\text{CM}}\ne R\alpha ,\,\text{and}\, {d}_{\text{CM}}\ne R\theta[/latex].
- Энергосбережение можно использовать для анализа качения.
 Энергия сохраняется при качении без проскальзывания. Энергия не сохраняется при качении с проскальзыванием из-за тепла, выделяемого кинетическим трением.
Энергия сохраняется при качении без проскальзывания. Энергия не сохраняется при качении с проскальзыванием из-за тепла, выделяемого кинетическим трением.
Концептуальные вопросы
Может ли круглый объект, выведенный из состояния покоя на вершине склона без трения, совершить качение?
Показать решение
Цилиндрическая банка радиусом R катится по горизонтальной поверхности без проскальзывания. а) На какое расстояние переместится его центр масс после одного полного оборота банки? б) Будет ли это расстояние больше или меньше, если произойдет скольжение?
Колесо высвобождается сверху на уклоне. Колесо, скорее всего, будет скользить, если уклон будет крутым или пологим?
Показать решение
Что быстрее катится по наклонной плоскости, полый цилиндр или сплошной шар? Оба имеют одинаковую массу и радиус.
Полая сфера и полый цилиндр одинакового радиуса и массы катятся по склону без проскальзывания и имеют одинаковую начальную скорость центра масс. Какой объект достигает большей высоты, прежде чем остановиться?
Какой объект достигает большей высоты, прежде чем остановиться?
Показать решение
Задачи
Какова угловая скорость шины диаметром 75,0 см на автомобиле, движущемся со скоростью 90,0 км/ч?
Показать ответ
Мальчик проехал на велосипеде 2,00 км. Колеса имеют радиус 30,0 см. На какой общий угол поворачиваются шины во время его поездки?
Если мальчик на велосипеде в предыдущей задаче разгоняется из состояния покоя до скорости 10,0 м/с за 10,0 с, каково угловое ускорение шин?
Показать решение
Гоночные автомобили Формулы-1 имеют шины диаметром 66 см. Если Формула-1 развивает среднюю скорость 300 км/ч во время гонки, каково угловое смещение в оборотах колес, если гоночная машина поддерживает эту скорость в течение 1,5 часов?
Шарик скатывается по склону на [latex] 30\text{°} [/latex] из состояния покоя. а) Чему равно его ускорение? б) Какой путь он пройдет за 3,0 с?
Показать решение
Повторите предыдущую задачу, заменив шарик цельным цилиндром. Объясните новый результат.
Объясните новый результат.
Твердое тело с цилиндрическим поперечным сечением высвобождается из верхней части склона [латекс] 30\text{°} [/латекс]. Он опускается на 10,0 м за 2,60 с. Найти момент инерции тела через его массу m и радиус r.
Показать решение
Йо-йо можно представить в виде твердого цилиндра массой m и радиусом r , по окружности которого намотана легкая нить (см. ниже). Один конец нити зафиксирован в пространстве. Если цилиндр падает при разматывании струны без проскальзывания, каково ускорение цилиндра?
Сплошной цилиндр радиусом 10,0 см катится по склону с проскальзыванием. Угол наклона [латекс] 30\text{°}. [/latex] Коэффициент кинетического трения о поверхность 0,400. Чему равно угловое ускорение твердого цилиндра? Чему равно линейное ускорение?
Показать решение
Шар для боулинга катится по пандусу высотой 0,5 м, не соскальзывая при этом на хранение. Его начальная скорость центра масс равна 3,0 м/с. а) Какова его скорость на вершине рампы? б) Если пандус имеет высоту 1 м, дойдет ли он до вершины?
Его начальная скорость центра масс равна 3,0 м/с. а) Какова его скорость на вершине рампы? б) Если пандус имеет высоту 1 м, дойдет ли он до вершины?
Сплошной цилиндр массой 40,0 кг катится по горизонтальной поверхности со скоростью 6,0 м/с. Какая работа требуется, чтобы остановить его?
Показать решение
Твердый шар массой 40,0 кг катится по горизонтальной поверхности со скоростью 6,0 м/с. Какая работа требуется, чтобы остановить его? Сравните результаты с предыдущей задачей.
Сплошной цилиндр катится по склону под углом [латекс] 20\text{°}. [/latex] Если он стартует снизу со скоростью 10 м/с, как далеко он продвинется по склону?
Показать решение
Сплошное цилиндрическое колесо массой M и радиусом R притягивается силой [латекс] \overset{\to} {F} [/латекс], приложенной к центру колеса в точке [латекс] 37\ text{°} [/latex] по горизонтали (см. следующий рисунок).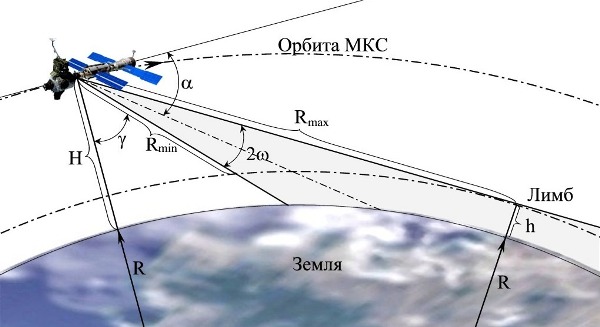

 [/латекс]
[/латекс] Для этого запишем второй закон Ньютона для вращения
Для этого запишем второй закон Ньютона для вращения [/latex] Таким образом, чем больше угол наклона, тем больше линейное ускорение, как и следовало ожидать. Угловое ускорение, однако, линейно пропорционально [латекс] \текст{sin}\,\тета [/латекс] и обратно пропорционально радиусу цилиндра. Таким образом, чем больше радиус, тем меньше угловое ускорение.
[/latex] Таким образом, чем больше угол наклона, тем больше линейное ускорение, как и следовало ожидать. Угловое ускорение, однако, линейно пропорционально [латекс] \текст{sin}\,\тета [/латекс] и обратно пропорционально радиусу цилиндра. Таким образом, чем больше радиус, тем меньше угловое ускорение. Энергия сохраняется при качении без проскальзывания. Энергия не сохраняется при качении с проскальзыванием из-за тепла, выделяемого кинетическим трением.
Энергия сохраняется при качении без проскальзывания. Энергия не сохраняется при качении с проскальзыванием из-за тепла, выделяемого кинетическим трением.