Квантование пространства-времени. Квантовое пространство

Атомы пространства и времени

Ли Смолин

Если удивительная теория петлевой квантовой гравитации верна, то пространство и время, воспринимаемые нами как непрерывные, на самом деле состоят из дискретных частиц.

С древних времен некоторые философы и ученые предполагали, что материя может состоять из крошечных атомов, но еще 200 лет назад мало кто верил, что их существование можно доказать. Сегодня мы наблюдаем отдельные атомы и изучаем частицы, их составляющие. Зернистое строение вещества для нас уже не новость.

В последние десятилетия физики и математики задаются вопросом: не из дискретных ли частей состоит пространство? Действительно ли оно непрерывно или больше похоже на кусок ткани, сотканной из отдельных волокон? Если бы мы могли наблюдать чрезвычайно малые объекты, то увидели бы атомы пространства, неделимые мельчайшие частицы объема? А как быть со временем: плавно ли происходят изменения в природе или мир развивается крошечными скачками, действуя словно компьютер?

За последние 16 лет ученые заметно приблизились к ответам на эти вопросы. Согласно теории со странным названием «петлевая квантовая гравитация», пространство и время действительно состоят из дискретных частей. Расчеты, выполненные в рамках этой концепции, описывают простую и красивую картину, которая помогает нам объяснить загадочные явления, относящиеся к черным дырам и Большому взрыву. Но главное достоинство упомянутой теории заключается в том, что уже в ближайшем будущем ее предсказания можно будет проверить экспериментально: мы обнаружим атомы пространства, если они действительно существуют.

Кванты

Вместе с моими коллегами мы развивали теорию петлевой квантовой гравитации (ПКГ), пытаясь разработать долгожданную квантовую теорию тяготения. Чтобы объяснить исключительную важность последней и ее отношение к дискретности пространства и времени, я должен немного рассказать о квантовой теории и теории гравитации.

Появление квантовой механики в первой четверти XX в. было связано с доказательством, что материя состоит из атомов. Квантовые уравнения требуют, чтобы некоторые величины, такие как энергия атома, могли принимать только определенные дискретные значения. Квантовая механика в точности описывает свойства и поведение атомов, элементарных частиц и связывающих их сил. Самая успешная в истории науки квантовая теория лежит в основе нашего понимания химии, атомной и субатомной физики, электроники и даже биологии.

В те же десятилетия, когда зарождалась квантовая механика, Альберт Эйнштейн разработал общую теорию относительности, которая представляет собой теорию гравитации. Согласно ей, сила тяготения возникает в результате изгиба пространства и времени (которые вместе образуют пространство-время) под действием материи.

Представьте себе тяжелый шар, помещенный на резиновый лист, и маленький шарик, который катается вблизи большого. Шары можно рассматривать как Солнце и Землю, а лист - как пространство. Тяжелый шар создает в резиновом полотне углубление, по склону которого меньший шарик скатывается к большему, как будто некоторая сила - гравитатация - тянет его в этом направлении. Точно так же любая материя или сгусток энергии искажают геометрию пространства-времени, притягивая частицы и световые лучи; это явление мы и называем гравитацией. По отдельности квантовая механика и общая теория относительности Эйнштейна экспериментально подтверждены. Однако еще ни разу не исследовался случай, когда можно было бы проверить обе теории одновременно. Дело в том, что квантовые эффекты заметны лишь в малых масштабах, а для того, чтобы стали заметны эффекты общей теории относительности, требуются большие массы. Объединить оба условия можно лишь при каких-то экстраординарных обстоятельствах. Помимо отсутствия экспериментальных данных существует огромная концептуальная проблема: общая теория относительности Эйнштейна полностью классическая, т.е. неквантовая. Для обеспечения логической целостности физики нужна квантовая теория гравитации, объединяющая квантовую механику с общей теорией относительности в квантовую теорию пространства-времени. Физики разработали множество математических процедур для превращения классической теории в квантовую. Многие ученые тщетно пытались применить их к общей теории относительности. Расчеты, проведенные в 1960-х и 1970-х гг., свидетельствовали о том, что квантовую механику и общую теорию относительности объединить невозможно. Казалось, ситуацию может спасти только введение совершенно новых постулатов, дополнительных частиц, полей или объектов иного рода. Экзотика единой теории должна проявляться только в тех исключительных случаях, когда существенными становятся и квантово-механические, и гравитационные эффекты. В попытках достижения компромисса родились такие направления, как теория твисторов, некоммутативная геометрия и супергравитация. Большой популярностью у физиков пользуется теория струн, согласно которой помимо трех хорошо известных пространственных измерений есть еще шесть или семь, которые до сих пор никому не удавалось заметить. Теория струн также предсказывает существование множества новых элементарных частиц и сил, наличие которых еще ни разу не было подтверждено наблюдениями. Некоторые ученые полагают, что она является частью так называемой М-теории, но, к сожалению, никакого точного ее определения пока предложено не было. Поэтому многие специалисты убеждены, что следует изучить имеющиеся альтернативы. Наша петлевая квантовая теория гравитации - наиболее развитая из них.

Большая лазейка

В середине 1980-х гг. мы вместе с Аби Аштекером (Abhay Ashtekar), Тэдом Джекобсоном (Ted Jacobson) и Карло Ровелли (Carlo Rovelli) решили еще раз попытаться объединить квантовую механику и общую теорию относительности с помощью стандартных методов. Дело в том, что в отрицательных результатах, полученных в 1970-х гг., оставалась важная лазейка: при расчетах предполагалось, что геометрия пространства непрерывная и гладкая независимо от того, насколько детально мы исследуем ее. Точно также люди рассматривали вещество до открытия атомов.

Итак, мы решили отказаться от концепции гладкого непрерывного пространства и не вводить никаких гипотез, кроме хорошо проверенных экспериментально положений общей теории относительности и квантовой механики. В частности, в основе наших расчетов были заложены два ключевых принципа теории Эйнштейна. Первый из них - независимость от окружения - провозглашает, что геометрия пространства-времени не фиксирована, а является меняющейся, динамической величиной. Чтобы определить геометрию, необходимо решить ряд уравнений, учитывающих влияние вещества и энергии. Кстати, современная теория струн не является независимой от окружения: уравнения, описывающие струны, сформулированы в определенном классическом (т.е. неквантовом) пространстве-времени.

Второй принцип, названный «диффеоморфной инвариантностью», гласит, что для отображения пространства-времени и построения уравнений мы вольны выбирать любую систему координат. Точка в пространстве-времени задается только физически происходящими в ней событиями, а не ее положением в какой-то особой системе координат (не существует никаких особых координат). Диффеоморфная инвариантность - чрезвычайно важное фундаментальное положение общей теории относительности.

Аккуратно объединив оба принципа со стандартными методами квантовой механики, мы разработали математический язык, который позволил провести нужные вычисления и выяснить, дискретно пространство или непрерывно. К нашему восторгу, из расчетов следовало, что пространство квантовано! Так мы заложили основу теории петлевой квантовой гравитации. Кстати, термин «петлевая» был введен из-за того, что в некоторых вычислениях использовались маленькие петли, выделенные в пространстве-времени.

Многие физики и математики проверили наши расчеты с использованием различных методов. За прошедшие годы теория петлевой квантовой гравитации окрепла благодаря усилиям ученых разных стран мира. Проделанная работа позволяет нам доверять той картине пространства-времени, которую я опишу ниже.

В нашей квантовой теории речь идет о структуре пространства-времени в самых малых масштабах, и чтобы разобраться в ней, необходимо рассматривать ее предсказания для маленькой площади или объема. Имея дело с квантовой физикой, важно определить, какие физические величины должны быть измерены. Представьте себе некую область, обозначенную границей В (см. рис. внизу), которая может быть задана материальным объектом (например, чугунной скорлупой) или непосредственно геометрией пространства-времени (например, горизонтом событий в случае черной дыры). Что происходит, когда мы измеряем объем описанной области? Каковы возможные результаты, допускаемые как квантовой теорией, так и диффеоморфной инвариантностью? Если геометрия пространства непрерывна, то рассматриваемая область может иметь любой размер, и ее объем может быть выражен любым действительным положительным числом, в частности, сколь угодно близким к нулю. Но если геометрия гранулированa, то результат измерения может принадлежать только дискретному набору чисел и не может быть меньше некоторого минимально возможного объема. Давайте вспомним, какой энергией может обладать электрон, обращающийся вокруг атомного ядра? В рамках классической физики - любой, но квантовая механика допускает только определенные, строго фиксированные дискретные значения энергии. Различие такое же, как между измерением объема жидкости, образующей непрерывный поток (с точки зрения ученых XVIII в.), и определением количества воды, атомы которой можно сосчитать.

Согласно теории петлевой квантовой гравитации, пространство подобно атомам: числа, получаемые при измерении объема, образуют дискретный набор, т.е. объем изменяется отдельными порциями. Другая величина, которую можно измерить, - площадь границы В, которая тоже оказывается дискретной. Иными словами, пространство не непрерывно и состоит из определенных квантовых единиц площади и объема. Возможные значения объема и площади измеряются в единицах, производных от длины Планка, которая связана с силой гравитации, величиной квантов и скоростью света. Длина Планка очень мала: 10^-33 см; она определяет масштаб, при котором геометрию пространства уже нельзя считать непрерывной. Самая маленькая возможная площадь, отличная от нуля, примерно равна квадрату длины Планка или 10^-66 см2. Наименьший возможный объем, отличный от нуля, - куб длины Планка или 10^-99 см3. Таким образом, согласно теории в каждом кубическом сантиметре пространства содержится приблизительно 10^99 атомов объема. Квант объема настолько мал, что в кубическом сантиметре таких квантов больше, чем кубических сантиметров в видимой Вселенной (10^85).

Спиновые сети

На что же похожи кванты объема и площади? Быть может, пространство состоит из огромного количества крошечных кубов или сфер? Нет, не все так просто. Квантовые состояния объема и площади мы изображаем в виде диаграмм, которые не лишены своеобразной красоты. Вообразите область пространства, по форме напоминающую куб (см. рис. внизу). На диаграмме мы изображаем ее как точку, представляющую объем, с шестью выходящими из нее линиями, каждая из которых изображает одну из граней куба. Число рядом с точкой указывает величину объема, а числа рядом с линиями - величину площади соответствующих граней.

Поместим на вершину куба пирамиду. У наших многогранников есть общая грань, и их следует изобразить как две точки (два объема), соединенные одной из линий (грань, которая соединяет объемы). У куба осталось пять свободных граней (пять линий), а у пирамиды - четыре (четыре линии). Аналогично можно изобразить любые комбинации различных многогранников: объемные полиэдры становятся точками или узлами, а плоские грани - линиями, соединяющими узлы. Математики называют такие диаграммы графами.

В нашей теории мы отбрасываем рисунки многогранников и оставляем только графы. Математика, описывающая квантовые состояния объема и площади, обеспечивает нас набором правил, указывающих, как линии могут соединять узлы и какие числа могут располагаться в различных местах диаграммы. Каждое квантовое состояние соответствует одному из графов, и каждому графу, удовлетворяющему правилам, соответствует квантовое состояние. Графы представляют собой удобную краткую запись возможных квантовых состояний пространства.

Диаграммы гораздо больше подходят для представления квантовых состояний, чем многогранники. В частности, некоторые графы соединяются такими странными способами, что их невозможно аккуратно преобразовать в картину из полиэдров. Например, в тех случаях, когда пространство изогнуто, невозможно изобразить многогранники, стыкующиеся должным образом, зато совсем не трудно нарисовать граф и по нему вычислить, насколько искажено пространство. Поскольку именно искажение пространства создает гравитацию, диаграммы играют огромную роль в квантовой теории тяготения.

Для простоты мы часто рисуем графы в двух измерениях, но лучше представлять их заполняющими трехмерное пространство, потому что именно его они изображают. Но здесь есть концептуальная ловушка: линии и узлы графа не занимают конкретные положения в пространстве. Каждый граф определяется только тем, как его части соединяются между собой и как они соотносятся с четко заданными границами (например, с границей области B). Однако нет никакого непрерывного трехмерного пространства, в котором, как может показаться, размещаются графы. Линии и узлы - это и есть пространство, геометрия которого определяется тем, как они соединяются.

Описанные графы называются спиновыми сетями, потому что указанные на них числа связаны со спином. Еще в начале 1970-х гг. Роджер Пенроуз (Roger Penrose) из Оксфордского университета предположил, что спиновые сети имеют отношение к теории квантовой гравитации. В 1994 г. наши точные вычисления подтвердили его интуитивную догадку. Читатели, знакомые с диаграммами Фейнмана, должны обратить внимание, что спиновые сети ими не являются, несмотря на внешнее сходство. Диаграммы Фейнмана отражают квантовые взаимодействия между частицами, переходящими из одного квантового состояния в другое. Спиновые сети олицетворяют фиксированные квантовые состояния объемов и площадей пространства.

Отдельные узлы и ребра диаграмм представляют собой чрезвычайно малые области пространства: типичный узел соответствует объему около одной длины Планка в кубе, а линия - площади порядка одной длины Планка в квадрате. Но, в принципе, спиновая сеть может быть неограниченно большой и сколь угодно сложной. Если бы мы могли изобразить детальную картину квантового состояния нашей Вселенной (т.е. геометрию ее пространства, искривленного и перекрученного тяготением галактик, черных дыр и пр.), то получилась бы гигантская спиновая сеть невообразимой сложности, содержащая приблизительно 10^184 узлов.

Итак, спиновые сети описывают геометрию пространства. Но что можно сказать о материи и энергии, находящихся в нем? Частицы, такие как электроны, соответствуют определенным узлам, снабженным дополнительными метками. Поля, такие как электромагнитное, обозначаются аналогичными маркерами на линиях графа. Движение частиц и полей в пространстве представляет собой дискретное (скачкообразное) перемещение меток по графу.

Шаги и пена

Частицы и поля - не единственные движущиеся объекты. Согласно общей теории относительности, при перемещении материи и энергии пространство модифицируется, по нему даже могут проходить волны, подобно ряби на озере. В теории петлевой квантовой гравитации такие процессы изображаются дискретными трансформациями спиновой сети, при которых шаг за шагом изменяется связность графов (см. рис. внизу).

При описании квантово-механических явлений физики вычисляют вероятность различных процессов. Мы делаем то же самое, когда применяем теорию петлевой квантовой гравитации, чтобы описать изменение геометрии пространства или движение частиц и полей в спиновой сети. Томас Тиманн (Thomas Thiemann) из Института теоретической физики в Ватерлоо вывел точные выражения для вычисления квантовой вероятности шагов спиновой сети. В результате появилась четкая процедура для вычисления вероятности любого процесса, который может происходить в мире, подчиняющемся правилам нашей, теперь уже окончательно сформировавшейся теории. Остается только вычислять и делать предсказания о том, что можно будет наблюдать в тех или иных экспериментах.

В теории относительности пространство и время неотделимы и представляют собой единое пространство-время. При введении концепции пространства-времени в теорию петлевой квантовой гравитации спиновые сети, представляющие пространство, превращаются в так называемую спиновую пену. С добавлением еще одного измерения - времени - линии спиновой сети расширяются и становятся двумерными поверхностями, а узлы растягиваются в линии. Переходы, при которых происходит изменение спиновой сети (шаги, описанные выше), теперь представлены узлами, в которых сходятся линии пены. Взгляд на пространство-время как на спиновую пену был предложен несколькими исследователями, в том числе Карло Ровелли (Carlo Rovelli), Майком Рейзенбергером (Mike Reisenberger), Джоном Бэрретом (John Barrett), Луи Крейном (Louis Crane), Джоном Бейзом (John Baez) и Фотини Маркопулу (Fotini Markopoulou).

Мгновенный снимок происходящего подобен поперечному срезу пространства-времени. Аналогичный срез спиновой пены представляет собой спиновую сеть. Однако не стоит заблуждаться, что плоскость среза перемещается непрерывно подобно плавному потоку времени. Также как пространство определяется дискретной геометрией спиновой сети, время задается последовательностью отдельных шагов, которые перестраивают сеть (см. рис. на стр. 55). Таким образом, время тоже дискретно. Время не течет, как река, а тикает, как часы. Интервал между «тиками» примерно равен времени Планка, или 10^-43 с. Точнее говоря, время в нашей Вселенной отмеряют мириады часов: там, где в спиновой пене происходит квантовый шаг, часы делают один «тик».

Предсказания и проверки

Теория петлевой квантовой гравитации описывает пространство и время в масштабе Планка, который слишком мал для нас. Так как же нам проверить ее? Во-первых, очень важно выяснить, можно ли вывести классическую общую теорию относительности как приближение к петлевой квантовой гравитации. Другими словами, если спиновые сети подобны нитям, из которых соткана ткань, то вопрос стоит так: удастся ли правильно вычислить упругие свойства куска материала путем усреднения по тысячам нитей. Получим ли мы описание «гладкой ткани» классического эйнштейновского пространства, если усредним спиновую сеть по многим длинам Планка? Недавно ученые успешно решили эту сложнейшую задачу для нескольких частных случаев, так сказать, для некоторых конфигураций материала. Например, низкочастотные гравитационные волны, распространяющиеся в плоском (неизогнутом) пространстве, можно рассматривать как возбуждение определенных квантовых состояний, описанных в соответствии с теорией петлевой квантовой гравитации. Хорошей проверкой для петлевой квантовой гравитации оказалась одна из давнишних загадок о термодинамике черных дыр, и в особенности об их энтропии. Физики разработали термодинамическую модель черной дыры, опираясь на гибридную теорию, в которой материя рассматривается квантово-механически, а пространство-время - нет. В частности, в 1970-х гг. Якоб Бекенштейн (Jacob D. Bekenstein) вывел, что энтропия черной дыры пропорциональна площади ее поверхности (см. статью «Информация в голографической Вселенной», «В мире науки», №11, 2003 г.). Вскоре Стивен Хокинг (Stephen Hawking) пришел к выводу, что черные дыры, особенно маленькие, должны излучать.

Чтобы выполнить аналогичные вычисления в рамках теории петлевой квантовой гравитации, мы принимаем границу области В за горизонт событий черной дыры. Анализируя энтропию соответствующих квантовых состояний, мы получаем в точности предсказание Бекенштейна. С таким же успехом наша теория не только воспроизводит предсказание Хокинга об излучении черной дыры, но и позволяет описать его тонкую структуру. Если когда-либо удастся наблюдать микроскопическую черную дыру, теоретические предсказания можно будет проверить, изучая спектр ее излучения.

Вообще говоря, любая экспериментальная проверка теории петлевой квантовой гравитации сопряжена с колоссальными техническими трудностями. Характерные эффекты, описываемые теорией, становятся существенными только в масштабе длины Планка, который на 16 порядков меньше, чем можно будет исследовать в ближайшее время на самых мощных ускорителях (для исследования меньших масштабов необходима более высокая энергия).

Впрочем, недавно ученые предложили несколько доступных способов проверки петлевой квантовой гравитации. Длина световой волны, распространяющейся в среде, претерпевает искажения, что приводит к преломлению и дисперсии лучей. Аналогичные метаморфозы происходят со светом и частицами, движущимися через дискретное пространство, описываемое спиновой сетью.

К сожалению, величина упомянутых эффектов пропорциональна отношению длины Планка к длине волны. Для видимого света оно не превышает 10^-28, а для космических лучей с наибольшей энергией составляет порядка одной миллиардной. Иными словами, зернистость структуры пространства чрезвычайно слабо сказывается практически на любом наблюдаемом излучении. Но чем большее расстояние прошел свет, тем сильнее заметны последствия дискретности спиновой сети. Современная аппаратура позволяет нам регистрировать излучение гамма-всплесков, расположенных в миллиардах световых лет (см. статью «Ярчайшие взрывы во Вселенной», «В мире науки», №4,2003 г.).

Опираясь на теорию петлевой квантовой гравитации, Родольфо Гамбини (Rodolfo Gambini) и Джордж Пуллин (Jorge Pullin) установили, что фотоны различных энергий должны перемещаться с несколько разными скоростями и достигать наблюдателя в разное время (см. рис. внизу). Спутниковые наблюдениях гамма-всплесков помогут нам проверить это. Точность современных приборов в 1 000 раз ниже необходимой, но уже в 2006 г. будет запущена спутниковая обсерватория GLAST, прецизионное оборудование которой позволит провести долгожданный эксперимент.

Нет ли здесь противоречия с теорией относительности, в которой постулируется постоянство скорости света? Вместе с Джованни Амелино-Камелиа (Giovanni Amelino-Camelia) и Хояо Магуэйо (Joao Magueijo) мы разработали модифицированные версии теории Эйнштейна, которые допускают существование фотонов высокой энергии, движущихся с разными скоростями. В свою очередь постоянство скорости относится к фотонам низких энергий, т.е. к длинноволновому свету.

Другое возможное проявление дискретности пространства-времени связано с космическими лучами очень высокой энергии. Более 30 лет назад ученые установили, что протоны космических лучей с энергией более 3*10^19 эВ должны рассеиваться на космическом микроволновом фоне, заполняющем пространство, и поэтому никогда не достигнут Земли. Тем не менее в японском эксперименте AGASA было зарегистрировано более 10 событий с космическими лучами даже большей энергии. Оказалось, что дискретность пространства повышает энергию, требуемую для реакции рассеивания, и позволяет высокоэнергетическим протонам навещать нашу планету. Если наблюдения японских ученых подтвердятся, а другое объяснение не будет найдено, то можно будет считать, что дискретность пространства засвидетельствована экспериментально.

Космос

Теория петлевой квантовой гравитации заставляет нас по-новому взглянуть на происхождение Вселенной и помогает представить, что происходило сразу после Большого взрыва. В соответствии с общей теорией относительности в истории мироздания был самый первый, нулевой момент времени, что не согласуется с квантовой физикой. Расчеты, проведенные Мартином Боджовальдом (Martin Bojowald) на основании теории петлевой о квантовой гравитации, указывают, что Большой взрыв фактически был Большим отскоком, так как до него Вселенная быстро сжималась. Теоретики уже работают над новыми моделями ранней стадии развития Вселенной, которые вскоре можно будет проверить в космологических наблюдениях. Не исключено, что нам с вами еще посчастливится узнать, что же происходило до Большого взрыва.

Не менее серьезно стоит вопрос о космологической постоянной: положительна или отрицательна плотность энергии, пронизывающей «пустое» пространство? Результаты наблюдения реликтового фона и далеких сверхновых свидетельствуют о том, что темная энергия существует. Более того, она положительна, поскольку Вселенная расширяется с ускорением. С точки зрения теории петлевой квантовой гравитации, здесь нет никакого противоречия: еще в 1990 г. Хидео Кодама (Hideo Kodama) составил уравнения, точно описывающие квантовое состояние Вселенной с положительной космологической постоянной. До сих пор еще не решен целый ряд вопросов, в том числе чисто технических. Какие коррективы следует вносить в частную теорию относительности при чрезвычайно высоких энергиях (если вообще следует)? Поможет ли теория петлевой квантовой гравитации доказать, что различные силы, включая тяготение, являются аспектами единственного фундаментального взаимодействия?

Быть может, петлевая квантовая гравитация - это действительно квантовая общая теория относительности, потому что в ее основе нет никаких дополнительных предположений, кроме основных принципов квантовой механики и теории Эйнштейна. Вывод о дискретности пространства-времени, описываемого спиновой пеной, следует непосредственно из самой теории, а не вводится как постулат.

Однако все, о чем я здесь рассуждал, - это теория. Возможно, пространство на самом деле гладко и непрерывно в любых, сколь угодно малых масштабах. Тогда физикам придется ввести дополнительные радикальные постулаты, как в случае теории струн. А поскольку в конечном счете все решит эксперимент, у меня есть хорошие новости - ситуация может проясниться в ближайшее время.

Дополнительная литература:

1. Three Roads to Quantum Gravity. Lee Smolin. Basic Books, 2001. 2. The Quantum of Area? John Baez. Nature, vol.421, pp. 702-703; February 2003. 3. How Far Are We from the Quantum Theory of Gravity? Lee Smolin. March 2003. Препринт на сайте http://arxiv.org/hep-th/0303185 4. Welcome to Quantum Gravity. Special Section, Physics World, Vol.16, No.11, pp. 27-50; November 2003. 5. Loop Quantum Gravity. Lee Smolin. Доступно на сайте http://www.edge.org/3rd_culture/smolin03/smolin03_index.html

ГЛАВНЫЙ ВЫВОД теории петлевой квантовой гравитации относится к объемам и площадям. Рассмотрим область пространства, ограниченную сферической оболочкой В (см. сверху). В соответствии с классической (неквантовой) физикой ее объем может выражаться любым действительным положительным числом. Однако, согласно теории петлевой квантовой гравитации, существует отличный от нуля абсолютный наименьший объем (примерно равный кубу длины Планка, т.е. 10^99 см3), а значения больших объемов представляют собой дискретный ряд чисел. Аналогично, есть ненулевая минимальная площадь (примерно квадрат длины Планка или 10^66 см2) и дискретный ряд допустимых площадей большего размера. Дискретные спектры допустимых квантовых площадей (слева) и квантовых объемов (в центре) в широком смысле похожи на дискретные квантовые уровни энергии атома водорода (справа).

Изображение квантового состояния объёма

ДИАГРАММЫ, НАЗЫВАЕМЫЕ СПИНОВЫМИ СЕТЯМИ, используются для представления квантовых состояний пространства при минимальном масштабе длины. Например, куб (а) - это объем, окруженный шестью квадратными гранями. Соответствующая спиновая сеть (b) содержит точку (узел), представляющую объем, и шесть линий, изображающих грани. Число возле узла указывает величину объема, а число возле линии - площадь соответствующей грани. В рассматриваемом случае объем равен восьми кубическим единицам Планка, а каждая из граней имеет площадь в четыре квадратные единицы Планка. (Правила петлевой квантовой гравитации ограничивают допустимые значения объемов и площадей определенными величинами: у линий и в узлах могут располагаться лишь определенные комбинации чисел.)

Если на верхней грани куба помещена пирамида (с), то линия, представляющая эту грань в спиновой сети, должна соединять узел куба с узлом пирамиды (d). Линии, соответствующие четырем свободным граням пирамиды и пяти свободным граням куба, должны выходить из соответствующих узлов. (Для упрощения схемы числа опущены.)

Вообще в спиновой сети один квант площади изображается одной линией (е), а площадь, составленная из многих квантов, обозначается многими линиями (f). Аналогично один квант объема изображается одним узлом (g), тогда как больший объем содержит много узлов (h), Так, объем внутри сферической оболочки задается суммой всех заключенных в ней узлов, а площадь поверхности равна сумме всех линий, проходящих сквозь границу области.

Спиновые сети более фундаментальны, чем конструкции из многогранников: любое сочетание полиэдров можно изобразить соответствующей диаграммой, но некоторые правильные спиновые сети представляют такие комбинации объемов и площадей, которые невозможно составить из многогранников. Такие спиновые сети возникают, когда пространство искривляется сильным гравитационным полем или квантовыми флуктуациями геометрии в планковских масштабах.

Эволюция геометрии во времени

ИЗМЕНЕНИЕ ФОРМЫ пространства при перемещении в нем материи и энергии и при прохождении через него гравитационных волн изображается дискретными перестройками, шагами спиновой сети. На рис. а связанная группа из трех квантов объема сливается в один; возможен и обратный процесс. На рис. b два объема разделяют пространство и соединяются с соседними объемами иным способом. При изображении в виде полиэдров два многогранника объединяются по их общей грани, а затем расщепляются, как при раскалывании кристаллов по другой плоскости. Такие шаги в спиновой сети происходят не только при больших изменениях геометрии пространства, но и при непрерывных квантовых флуктуациях в планковском масштабе.

Другой способ изображения шагов заключается в добавлении к диаграмме еще одной размерности - времени. В результате получается спиновая пена (с). Линии спиновой сети становятся плоскостями, а узлы превращаются в линии. Срез спиновой пены в определенный момент времени представляет собой спиновую сеть. Сделав ряд таких срезов, мы получим кадры фильма, повествующего о развитии спиновой сети во времени (d). Но обратите внимание, что эволюция, которая на первый взгляд кажется плавной и непрерывной, на самом деле идет скачками. Все спиновые сети, содержащие оранжевую линию (первые три кадра), отображают в точности одну и ту же геометрию пространства, Длина линий не имеет значения -для геометрии важно лишь то, как соединяются линии и каким числом отмечена каждая из них. Именно этим и определяется взаимное расположение и величина квантов объема и площади. Так, на рис, d в течение трех первых кадров геометрия остается постоянной - 3 кванта объема и 6 квантов площади. Затем пространство изменяется скачкообразно: остается 1 квант объема и 3 кванта площади, как показано на последнем кадре. Таким образом, время, определяемое спиновой пеной, изменяется не непрерывно, а последовательностью внезапных дискретных шагов.

И хотя для наглядности такие последовательности показаны как кадры фильма, правильнее рассматривать эволюцию геометрии как дискретное постукивание часов. При одном «тике» оранжевый квант площади есть; при следующем - он исчез: фактически его исчезновение и определяет «тик». Интервал между последовательными «тиками» примерно равен времени Планка (10^-43 с), но между ними время не существует; не может быть никакого «между», так же как нет воды между двумя соседними молекулами Н2O.

Экспериментальная проверка

КОГДА В МИЛЛИАРДАХ световых лет от нас происходит гамма-всплеск, мгновенный взрыв порождает гигантское количество гамма-лучей. В соответствии с теорией петлевой квантовой гравитации фотон, движущийся по спиновой сети, в каждый момент времени занимает несколько линий, т.е. некоторое пространство (в реальности на квант света приходится очень много линий, а не пять, как показано на рисунке). Дискретная природа пространства заставляет гамма-лучи более высокой энергии перемещаться немного быстрее. Разница ничтожна, но в ходе космического путешествия эффект накапливается миллиардами лет. Если возникшие при всплеске гамма-лучи разных энергий прибывают на Землю в разные моменты времени, то это свидетельствует в пользу теории петлевой квантовой гравитации.

Источник: "В мире науки"

scientifically.info

10 загадок пространства-времени, которые сможет решить квантовая гравитация

Общая теория относительности Эйнштейна, в которой гравитация рождается вследствие искривления пространства-времени, замечательна. Она была подтверждена с невероятным уровнем точности, в некоторых случаях до пятнадцати знаков после запятой. Одним из самых интересных ее предсказаний было существование гравитационных волн: ряби в пространстве-времени, которая свободно распространяется. Не так давно эти волны были пойманы детекторами LIGO и VIRGO.

И все же существует много вопросов, ответов на которые у нас пока нет. Квантовая гравитация могла бы помочь их найти.

Мы знаем, что общая теория относительности неполна. Она хорошо проявляет себя, когда квантовые эффекты пространства-времени совсем незаметны, а это почти всегда. Но когда квантовые эффекты пространства-времени становятся большими, нам нужна теория получше: теория квантовой гравитации.

Иллюстрация ранней Вселенной, состоящей из квантовой пены, когда квантовые флуктуации были огромными и проявлялись на мельчайших масштабах

Поскольку мы пока не составили теорию квантовой гравитации, мы не знаем, что такое пространство и время. У нас есть несколько подходящих теорий для квантовой гравитации, но ни одна из них не принята широко. Тем не менее, исходя из существующих подходов, мы можем предположить, что может произойти с пространством и временем в теории квантовой гравитации. Физик Сабина Хоссфендер собрала десять поразительных примеров.

1) В квантовой гравитации в пространстве-времени будут дикие флуктуации даже в отсутствие вещества. В квантовом мире вакуум никогда не пребывает в состоянии покоя, равно как и пространство и время.

На самых малых квантовых масштабах Вселенная может быть заполнена крошечными микроскопическими черными дырами с малыми массами. Эти дыры могут соединяться или расширяться внутрь в весьма интересной манере

2) Квантовое пространство-время может быть заполнено микроскопическими черными дырами. Более того, в нем могут быть червоточины или рождаться младенческие вселенные – как маленькие пузырьки, которые отрываются от материнской вселенной.

3) И поскольку это квантовая теория, пространство-время может делать все это одновременно. Оно может одновременно создавать младенческую вселенную и не создавать ее.

Ткань пространства-времени может быть вовсе не тканью, а состоять из дискретных компонентов, которые лишь кажутся нам непрерывной тканью на больших макроскопических масштабах.

4) В большинстве подходов к квантовой гравитации, пространство-время не фундаментально, а состоит из чего-то еще. Это могут быть струны, петли, кубиты или варианты «атомов» пространства-времени, которые появляются в подходах с конденсированной материей. Отдельные составляющие можно разобрать лишь с применением высочайших энергий, намного превышающих те, что доступны нам на Земле.

5) В некоторых подходах с конденсированной материей пространство-время обладает свойствами твердого или жидкого тела, то есть может быть эластичным или вязким. Если это действительно так, неизбежны наблюдаемые последствия. Физики в настоящее время ищут следы подобных эффектов в странствующих частицах, то есть в свете или электронах, которые добираются к нам из далекого космоса.

Схематическая анимация непрерывного луча света, рассеиваемого призмой. В некоторых подходах к квантовой гравитации пространство может выступать как дисперсионная среда для различных длин волн света

6) Пространство-время может влиять на то, как свет через него проходит. Оно может не быть полностью прозрачным, либо же свет разных цветов может двигаться с разной скоростью. Если квантовое пространство-время влияет на распространение света, это тоже можно будет наблюдать в будущих экспериментах.

7) Флуктуации пространства-времени могут разрушать способность света от удаленных источников создавать интерференционные картины. Этот эффект искали и не нашли, по крайней мере в видимом диапазоне.

Свет, проходящий через две толстые щели (сверху), две тонкие щели (в центре) или одну толстую щель (снизу), демонстрирует интерференцию, указывающую на его волновую природу. Но в квантовой гравитации некоторые ожидаемые интерференционные свойства могут быть невозможны

8) В областях сильной кривизны время может превращаться в пространство. Это может происходить, например, внутри черных дыр или при большом взрыве. В таком случае известное нам пространство-время с тремя пространственными и измерениями и одним временным может превращаться в четырехмерное «евклидово» пространство.

Соединение двух разных мест в пространстве или времени через червоточину остается лишь теоретической идеей, но она может быть не просто интересной, но и неизбежной в квантовой гравитации

Пространство-время может быть нелокально связано с крошечными червоточинами, пронизывающими всю вселенную. Такие нелокальные соединения должны существовать во всех подходах, чья базовая структура не является геометрической вроде графа или сети. Это связано с тем, что в таких случаях понятие «близости» будет не фундаментальным, а вытекающим и несовершенным, так что удаленные области могут быть случайно связанными.

10) Возможно, чтобы объединить квантовую теорию с гравитацией, нам нужно обновить не гравитацию, а саму квантовую теорию. Если это так, последствия будут далеко идущими. Поскольку квантовая теория лежит в основе всех электронных устройств, ее пересмотр откроет совершенно новые возможности.

Хотя квантовая гравитация часто рассматривается как сугубо теоретическая идея, существует множество возможностей для проведения экспериментальной проверки. Все мы путешествуем через пространство-время каждый день. Его понимание может изменить нашу жизнь.

hi-news.ru

Квантовая ткань пространства-времени: сеть-гобелен / Хабр

Как квантовые пары сшивают пространство-время

Первая часть

Брайан Свингл изучал физику в аспирантуре Массачусетского технологического института, когда он решил сходить на парочку занятий по теории струн, чтобы усовершенствовать своё образование – как он сам вспоминает, по принципу «почему бы и нет» – хотя изначально он не обращал внимания на концепции, с которыми он познакомился на этом курсе. Но погружаясь глубже, он начал замечать неожиданные связи с его собственной работой, в которой он использовал т.н. тензорные сети для предсказания свойств экзотических материалов и подход к физике чёрных дыр и квантовой гравитации, взятый из теории струн. «Я понял, что происходит нечто удивительное»,- говорит он.

Тензоры периодически неожиданно возникают в разных областях физики – это математические объекты, которые могут представлять множество чисел сразу. К примеру, вектор скорости – это простейший тензор: он включает как скорость, так и направление. Более сложные тензоры, связанные в сети, можно использовать для упрощения подсчетов для сложных систем, составленных из множества взаимодействующих частей – включая замысловатые взаимодействия огромного количества субатомных частиц, составляющих материю. Свингл – один из всё возрастающего количества физиков, видящих ценность применения тензорных сетей к космологии. Кроме других преимуществ, это может помочь разрешить продолжающийся спор о сущности пространства-времени. Джон Прескилл, профессор Ричарда Фейнмана по теоретической физике в КалТехе, считал, что многие физики подозревали о глубокой связи между квантовой запутанностью – пугающим дальнодействием, так рассердившим Эйнштейна – и геометрией пространства-времени на мельчайших масштабах. Это продолжается с тех пор, как Джон Уилер шестьдесят лет назад впервые описал пространство-время как пузырящуюся пену. «Если вы будете изучать геометрию на масштабах, сравнимых с планковскими» – на самых коротких возможных расстояниях – «оно всё меньше и меньше выглядит, как пространство-время»,- говорит Прескилл. «Это вообще уже не геометрия, а что-то другое, что-то, что возникает из более фундаментальных вещей».

Физики продолжают бороться с запутанной проблемой того, какой может быть эта более фундаментальная проблема, но они подозревают, что она связана с квантовой информацией. «Когда мы рассуждаем о кодировании информации, мы имеем в виду, что можно разделить систему на части и в ней будет существовать такая корреляция между ними, что я могу узнать что-либо об одной из частей, наблюдая за другой»,- говорит Прескилл. В этом и есть суть запутанности.

Часто говорят о «ткани» пространства-времени и эта метафора приводит к концепции сшивания отдельных нитей вместе для формирования гладкого целого. Эти нити по сути квантовые. «Запутанность – это ткань пространства-времени,- говорит Свингл, в данный момент работающий над исследованиями в Стэнфорде. – Это нить, связывающая всю систему вместе, обеспечивающая отличие общих свойств от свойств отдельных сущностей. Но чтобы на самом деле увидеть интересное совместное поведение, необходимо понять, как распределяется запутанность».

Тензорные сети предоставляют математический инструмент, способный делать именно это. С этой точки зрения, пространство-время возникает из наборов связанных друг с другом узлов сложной сети, где небольшие кусочки квантовой информации стыкуются друг с другом как Lego. Запутанность – это клей, соединяющий сеть. Чтобы понять пространство-время, необходимо для начала рассмотреть запутанность с геометрических позиций, поскольку именно так информация кодируется в огромном количестве взаимодействующих узлов системы.

Много тел, одна сеть

Смоделировать сложную квантовую систему – это вам не шутки; даже классическая система с более чем двумя взаимодействующими частями уже достаточно сложна для моделирования. Когда Исаак Ньютон опубликовал свои Principia [Математические начала натуральной философии] в 1687 году, одной из тем книги стала «задача трёх тел». Задача подсчёта движения двух объектов, например, Солнца и Земли, принимающая во внимание их взаимное притяжение, сравнительно проста. Но если добавить в неё третье тело – например, Луну – она превращается из простой задачи с точным решением в хаотичную, где долговременные предсказания требуют мощных вычислительных систем для симуляции приблизительной эволюции системы. И чем больше в системе объектов, тем сложнее расчёты, а их сложность растёт почти линейно – по крайней мере, в классической физике.

Теперь представим квантовую систему с миллиардами атомов, каждый из которых взаимодействует с другими согласно сложным квантовым уравнениям. На этом масштабе сложность, кажется, растёт экспоненциально с ростом количества частиц в системе, поэтому подход к вычислениям с применением грубой силы просто не сработает.

Представьте себе золотой самородок. Он состоит из миллиардов атомов, и все они взаимодействуют друг с другом. Из этих взаимодействий вытекают различные классические свойства металла – цвет, прочность или проводимость. «Атомы – это крохотные штучки, подчиняющиеся квантовой механике, и когда вы собираете их вместе, происходят новые и удивительные вещи»,- говорит Свингл. Но на этих масштабах начинают работать правила квантовой механики. Физикам необходимо точно подсчитать волновую функцию этого самородка, описывающую состояние системы. И эта функция – многоголовая гидра экспоненциальной сложности.

Даже если в самородке будет всего лишь сто атомов и у каждого будет квантовый спин, принимающий одно из двух состояний, вверх или вниз, общее количество возможных состояний составит уже 2100, миллион триллионов триллионов. И с добавлением каждого атома задача ухудшается экспоненциально. (А ещё хуже выходит, когда вы пытаетесь описать что-либо кроме спинов, как должна делать любая реалистичная модель). «Если вы возьмёте всю видимую Вселенную и заполните её лучшими из доступных вам накопителей, лучшими жёсткими дисками, вы сможете хранить на них состояние всего лишь 300 спинов,- говорит Свингл. – Информация есть, но не вся она соответствует физике. Никто никогда не мерил эти числа».

Тензорные сети позволяют физикам сжимать всю содержащуюся в волновой функции информацию и концентрироваться только на тех свойствах, которые можно измерить в эксперименте: как сильно материал преломляет свет, или как хорошо он поглощает звук, или как он проводит электричество. Тензор – это «чёрный ящик», принимающий один набор чисел и выдающий другой. Поэтому можно подключить простую волновую функцию – например, множества не взаимодействующих друг с другом электронов, находящихся в состоянии с наименьшей энергией – и обрабатывать её тензорами снова и снова, пока процесс не выдаст волновую функцию для большой и сложной системы, такой, как миллиарды взаимодействующих в золотом самородке атомов. В результате получится простая диаграмма, представляющая этот сложный самородок – инновация, сравнимая с разработанными Фейнманом в середине 20-го века диаграммами, упростившими представление взаимодействий частиц. И у тензорной сети есть своя геометрия, как и у пространства-времени.

Ключ к упрощению лежит в принципе «локальности». Каждый отдельно взятый электрон взаимодействует только с ближайшими электронами. Запутанность каждого электрона с его соседями даёт набор «узлов» сети. Эти узлы – тензоры и запутанность связывает их вместе. Все эти связанные между собой узлы составляют сеть. Сложные подсчёты становится проще визуализировать. Иногда всё сводится к более простой задаче подсчёта.

Существует множество разных типов тензорных сетей, но среди самых полезных есть одна, известная под аббревиатурой MERA (анзац ренормализации разномасштабной запутанности). Принцип её работы следующий: представьте одномерную линию электронов. Замените восемь разных электронов – обозначим их через A, B, C, D, E, F, G и H – на фундаментальные единицы квантовой информации (кубиты) и запутайте каждый из них с соседом, для образования связей. A запутывается с B, C – с D и так далее. Так получается сеть более высокого уровня. Затем запутайте AB с CD, а EF с GH, чтобы подняться ещё на один уровень сети. И, наконец, ABCD запутывается с EFGH для формирования самого высокого уровня. «В каком-то смысле можно сказать, что запутанность используется для построения волновой функции многих тел»,- писал в прошлом году в своей работе Роман Орус [Román Orús], физик из Университета им. Иоганна Гутенберга (Германия).

Почему же некоторые физики так оптимистично оценивают потенциал тензорных сетей – особенно MERA – способный привести их к квантовой гравитации? Поскольку сети показывают, как простая геометрическая структура может появиться из сложных взаимодействий между многими объектами. И Свингл с единомышленниками надеется, что эту новую геометрию удастся использовать, показав, как она объясняет механизм превращения отдельных кусочков квантовой информации в плавное, непрерывное пространство-время.

Границы пространства-времени

Специалисты по физике конденсированных сред при разработке тензорных сетей нечаянно обнаружили дополнительное измерение: эта техника приводит к появлению двумерных систем в одном измерении. А специалисты по теории гравитации убирали одно измерение – переходя от трёх к двум – разрабатывая т.н. голографический принцип. Две этих концепции могут объединиться и создать более сложное представление о пространстве-времени.

В 1970-х физик Джейкоб Бекенштейн [Jacob Bekenstein] показал, что информация о внутренности чёрной дыры закодирована на её плоской двумерной поверхности (на границе), а не в её трёхмерном объёме. Через двадцать лет Леонард Сасскинд и Герард ’т Хоофт [Leonard Susskind and Gerard ’t Hooft] расширили это понятие до всей Вселенной, приравняв её к голограмме: наша трёхмерная Вселенная во всём её великолепии возникает из двумерного «исходного кода». В 1997 Хуан Малдасена [Juan Maldacena] нашёл конкретный пример работы голограммы, продемонстрировав, что игрушечная модель описания плоского пространства без гравитации эквивалентна описанию седловидного пространства с гравитацией. Эту взаимосвязь физики называют «дуальностью».

Марк ван Раамсдонк [Mark Van Raamsdonk] представляет, как запутанность постепенно создаёт пространство-время. По краям фигуры отдельные частицы-точки начинают запутываться друг с другом. Эти запутанные пары запутываются с другими парами. По мере запутывания всё большего количества пар появляется структура пространства-времени.

Марк ван Раамсдонк, специалист по теории струн из Университета Британской Колумбии (Ванкувер), сравнивает этот голографический принцип с двумерным компьютерным чипом, содержащим код для создания трёхмерного виртуального мира в компьютерной игре. Мы живём внутри трёхмерного пространства игры. В каком-то смысле наше пространство иллюзорно и является лишь эфемерным изображением, висящим в воздухе. Но ван Раамсдонк подчёркивает, что «в компьютере всё-таки есть некая физическая сущность, хранящая всю информацию».

Идея получила широкое признание среди физиков-теоретиков, но они всё ещё сражаются с тем, как именно меньшие измерения хранят информацию о геометрии пространства-времени. Загвоздка в том, что наш метафорический компьютерный чип должен быть неким квантовым компьютером, в котором привычные нолики и единички заменены кубитами, способными одновременно представлять все возможные состояния от нуля до единицы. Эти кубиты должны быть запутаны – так, чтобы состояние одного кубита было определено состоянием его соседа – до того, как можно будет закодировать реалистичный трёхмерный мир.

Точно также запутанность выглядит фундаментальной особенностью пространства-времени. К этому выводу пришло двое учёных в 2006-м: Шинсей Рю [Shinsei Ryu] (Иллинойский университет) и Тадаши Такаянаги [Tadashi Takayanagi] (Киотский университет), поделившие в 2015 году премию «Новые горизонты физики». «Идея в том, что то, как кодируется геометрия пространства-времени, сильно связана с тем, как разные части этого чипа запутаны друг с другом»,- поясняет ван Раамсдонк.

Вдохновлённых их работой, а также последовавшей за ней работой Малдасены, в 2010-м году ван Раамсдонк предложил мысленный эксперимент, демонстрирующий критическую роль запутанности в формировании пространства-времени. Он исследовал, что случится, если поделить компьютерный чип пополам, а затем удалить запутанность между кубитами в двух половинках. Он обнаружил, что пространство-время начинает разрушаться так же, как растягивание кусочка жвачки за концы приводит к появлению разрыва в середине. Разделение этого чипа на всё более мелкие кусочки разрывает пространство время до тех пор, пока не остаются лишь отдельные, не связанные друг с другом кусочки. «Если убрать запутанность, пространство-время просто разваливается»,- говорит ван Раамсдонк. Точно так же, «если вы хотите построить пространство-время, вам придётся запутывать кубиты определённым образом».

Сложите эти мысли с работой Свингла, связывающей запутанную структуру пространства-времени и голографический принцип с тензорными сетями и ещё один кусочек головоломки встаёт на место. Искривлённое пространство-время естественным образом возникает из запутанности в тензорных сетях посредством голографии. «Пространство-время – это геометрическое представление этой квантовой информации»,- говорит ван Раамсдонк.

И как же выглядит эта геометрия? В случае седловидного пространства-времени Малдасены, она выглядит, как один из рисунков «предел – круг» Эшера из 1950-1960-х годов. Эшер долго интересовался порядком и симметрией, включая эти математические концепции в свои работы с 1936 года, когда он посетил архитектурно-парковый ансамбль Альгамбра в Испании и нашёл вдохновение в тамошних повторяющихся плиточных узорах, типичных для мавританской архитектуры, известных, как мозаика.

Его гравюры на дереве «предел – круг» иллюстрируют гиперболические геометрии: искажение пространства с отрицательной кривизной на двумерной поверхности диска напоминает уплощение глобуса до двумерной карты Земли, искажающее форму континентов. К примеру, "предел – круг IV" (ад и рай) выглядит, как множество повторяющихся фигурок ангелов и демонов. В гиперболическом пространстве размер всех фигур был бы одинаковым, но в двумерных представлениях Эшера фигурки у края выглядят меньше, чем в центре. Диаграмма тензорной сети очень сильно напоминает серию «предел – круг», визуальное представление глубоких связей, найденных Свинглом при посещении тех самых занятий по теории струн.

На сегодняшний день тензорный анализ ограничен моделированием пространства-времени (как у Малдасены), не описывающим ту Вселенную, в которой живём мы – она не имеет форму седла, а её расширение ускоряется. Физики могут переводить между моделями только в отдельных, особых случаях. В идеале им требуется универсальный «словарь». И им хотелось бы выводить этот словарь напрямую, не пользуясь приближениями. «С этими дуальностями мы оказались в забавном положении, потому что все соглашаются, что они очень важны, но никто не знает, как их выводить»,- говорит Прескилл. «Может, подход тензорных сетей сделает возможным дальнейшее продвижение. Думаю, признаком прогресса было бы, если бы мы могли сказать, пусть даже в случае игрушечной модели: 'Ага! Вот он, вывод словаря!'. Это был бы серьёзный намёк на то, что мы наткнулись на что-то важное».

За последний год Свингл и ван Раамсдонк работали вместе, чтобы продвинуть свои работы в область, выходящую из статичного представления пространства-времени в динамическое. Их интересует, как пространство-время изменяется со временем и как оно изгибается в ответ на эти изменения. Пока что им удалось вывести уравнения Эйнштейна, конкретно – принцип эквивалентности. Это доказывает, что динамика пространства-времени, как и его геометрия, основана на запутанных кубитах. Начало многообещающее.

«Вопрос 'Что такое пространство-время?' кажется абсолютно философским,- говорит ван Раамсдонк. – На самом деле найти на него ответ, конкретный и позволяющий вести расчёты пространства-времени – это было бы потрясающе».

habr.com

Квантование пространства и времени и его философские аспекты : Физика

Физики, не бейте меня ногами, если что ляпну: я сам математик, тополог, и отвечаю на оффтопик из нашей темы «Мнимые числа (философия в математике)».

Это микрообзор, но я размещаю его в «Дискуссионных темах», поскольку я эпизодически интересуюсь этой тематикой, и сейчас, пользуясь случаем, я решил рассказать о сформировавшейся в моей голове картине, чтобы, по семинарской привычке, в процессе формулирования своих мыслей сделать их яснее, по крайней мере, для себя, а также, в надежде, что может кто захочет сказать что-нибудь интересное. Т.е., как изъясняются психоаналитики, я хочу об этом поговорить. И, также, по своему семинарскому опыту, я хочу сразу предупредить об этом потенциального читателя.

Linkey

Цитата:

Вот ещё один глупый вопрос. Я привел как пример игру "Жизнь" - это вселенная, в которой имеют физическое воплощение только целые числа. А если пространство и время квантуются, можно ли то же сказать про нашу реальную вселенную? Т.е. длина - количество ячеек пространства, длительность - количество ячеек времени.

Здесь не простой вопрос, а целая проблема, и ответ на него я опять начну с экскурса в древнегреческую философию.

Атомарность. Само слово «атом» в переводе с древнегреческого означает «неделимый». А об учениях древнегреческих натурфилософов, стремящихся постигнуть природу всех вещей я писал реферат еще в далекие студенческие годы. Одним из стимулов к введению понятия атома, видимо, послужило желание разрешить апории Зенона Элейского, поскольку «Первый древнегреческий атомист, Левкипп, был учеником Зенона и одним из учителей другого крупного атомиста, Демокрита. Наиболее детальное изложение античного атомизма – система Эпикура, IV-III века до н. э. – дошло до нас в изложении Лукреция Кара . ... Эпикур считал мир дискретным, состоящим из вечно движущихся неделимых атомов и пустоты». Таким образом, вслед за древними греками, я буду понимать атомарность как наличие предела делимости.

Соответственно, я понимаю атомы пространства как элементы минимально возможных размеров. И, обратно, размер атома может задавать естественную меру пространства. Например, в подходе к количественному измерению пространства с Вами солидарен Адольф Грюнбаум, который в своей книге «Философские проблемы пространства и времени» пишет, что для атомарного пространства мера любого данного интервала могла бы быть выражена с помощью кардинального числа составляющих его атомов. Грюнбаум детально сравнивает измерение атомарного и неатомарного пространства на c.18-20 этой книги.

Впрочем, есть и довольно экзотический подход к этой проблеме. А.С. Кармин и В.И. Свидерский в книге «Конечное и бесконечное» (М.:Наука, 1966) пишут: «в теории Коиша - Шапиро пространственно-временная структура рассматривается как дискретная и состоящая из конечного (счетного) множества точек. “В ней само понятие длины применительно к микрообъектам утрачивает смысл; не имеют смысла и величина скорости распространения сигналов и метрические соотношения, определяющие в привычных нам “геоцентрических” условиях пространственную структуру, – они появляются лишь при предельном переходе к макрообъектам"».

Также, если считать пространство атомарным, то, поскольку положения движущегося тела в различные моменты своего движения нетождественны, то движение тела заключается в его перескакивании, между различными, хотя и очень мало отличающимися, положениями. Как, например, движение глайдера в «Жизни». (Хотя при рассмотрении движения тоже возникает интересная философская проблема самоидентичности движущего тела в разные моменты времени, но я должен себя сдерживать. ) С другой стороны, есть мнение, что в микромире единственный способ движения это движение волны, а не корпускулы.

Физическая бесконечность. Принятие или отвержение атомарности пространства тесно связано с принятием или отвержением физической бесконечности. Проблематичность того, что области пространства конечного объема могут состоять из бесконечного количества элементов пространства, и, в особенности, в то, что наличие этой бесконечности может быть обосновано исходя из экспериментальных данных, склоняют к атомарности пространства. Кстати, объединение принципа мереологического нигилизма, «согласно которому объекты, состоящие из частей, не существуют, а существуют только базовые объекты, которые не состоят из частей» с предположением о бесконечной делимости пространства слоняет к его онтологическому статусу не субстанции, а отношения.

С другой стороны, как я уже писал, Готфрид Вильгельм Лейбниц вводил физическую бесконечность во славу Господню, заявив: «Я в такой мере стою за актуальную бесконечность, что не только не допускаю, что природа боится ее, как обыкновенно выражаются, но и признаю, что природа всюду являет именно такую бесконечность, чтобы лучше отметить совершенство своего Творца» [Opera omnia studio Ludov. Dutens. Tom. II. part. I. p. 243].

Также обоснование наличия физической бесконечности может упираться в проблему индукции. Например, в статье «Квантовая гравитация» Брайс де Витт отмечает: «некоторые физики предположили, что общепринятое описание пространства-времени как гладкого континуума перестаёт быть правильным на планковском уровне и должно быть заменено чем-либо другим. Из чего складывается это «другое» — никогда не было достаточно ясно. Принимая во внимание успех общепринятого описания на расстояниях, простирающихся более чем на 40 порядков (или даже на 60 порядков, если считать, что такое описание становится неверным только при планковских расстояниях), можно предположить, что оно справедливо на всех масштабах и что топологических переходов просто не существует. Это будет столь же разумным предположением». Но что такое 40, или даже 60 порядков по сравнению с бесконечностью!

Поэтому, в итоге, лично я думаю, что в современных физических теориях бесконечности вводятся или рассматриваются не из-за онтологических оснований, а для удобства математического описания (как, например, та же сингулярность или бесконечные пространство и время современного понимания классической Ньютоновской механики).

Теория петлевой квантовой гравитации 1 – атомарность. Эта теория импонирует моему комбинаторно-графовому мышлению. Правда, у меня о ней довольно старые сведения из статьи Ли Смолина «Атомы пространства и времени», и я, краем уха, слышал, что позже у этой теории появились какие-то проблемы. Ли Смолин рассказывает: «В середине 1980-х гг. мы вместе с Аби Аштекером (Abhay Ashtekar), Тэдом Джекобсоном (Ted Jacobson) и Карло Ровелли (Carlo Rovelli) решили еще раз попытаться объединить квантовую механику и общую теорию относительности с помощью стандартных методов. Дело в том, что в отрицательных результатах, полученных в 1970-х гг., оставалась важная лазейка: при расчетах предполагалось, что геометрия пространства непрерывная и гладкая независимо от того, насколько детально мы исследуем ее. Точно также люди рассматривали вещество до открытия атомов.

Итак, мы решили отказаться от концепции гладкого непрерывного пространства и не вводить никаких гипотез, кроме хорошо проверенных экспериментально положений общей теории относительности и квантовой механики. В частности, в основе наших расчетов были заложены два ключевых принципа теории Эйнштейна.

Первый из них – независимость от окружения – провозглашает, что геометрия пространства-времени не фиксирована, а является меняющейся, динамической величиной. Чтобы определить геометрию, необходимо решить ряд уравнений, учитывающих влияние вещества и энергии. Кстати, современная теория струн не является независимой от окружения: уравнения, описывающие струны, сформулированы в определенном классическом (т.е. неквантовом) пространстве-времени.

Второй принцип, названный «диффеоморфной инвариантностью», гласит, что для отображения пространства-времени и построения уравнений мы вольны выбирать любую систему координат. Точка в пространстве-времени задается только физически происходящими в ней событиями, а не ее положением в какой-то особой системе координат (не существует никаких особых координат). Диффеоморфная инвариантность – чрезвычайно важное фундаментальное положение общей теории относительности.

Аккуратно объединив оба принципа со стандартными методами квантовой механики, мы разработали математический язык, который позволил провести нужные вычисления и выяснить, дискретно пространство или непрерывно. К нашему восторгу, из расчетов следовало, что пространство квантовано! Так мы заложили основу теории петлевой квантовой гравитации. Кстати, термин «петлевая» был введен из-за того, что в некоторых вычислениях использовались маленькие петли, выделенные в пространстве-времени.

Многие физики и математики проверили наши расчеты с использованием различных методов. За прошедшие годы теория петлевой квантовой гравитации окрепла благодаря усилиям ученых разных стран мира. Проделанная работа позволяет нам доверять той картине пространства-времени, которую я опишу ниже».

Однако, я обнаружил две интерпретации того, что же именно постулируется в теории петлевой квантовой гравитации.

Первая содержится в анонсе (да и в самом названии) приведенной выше статьи Ли Смолина: «Если удивительная теория петлевой квантовой гравитации верна, то пространство и время, воспринимаемые нами как непрерывные, на самом деле состоят из дискретных частиц», из атомов. И в самой статьи есть места, склоняющие меня именно к такой интерпретации.

Теория петлевой квантовой гравитации 2 – квантованность. Вторую интерпретацию приводит здесь akuklev, побывавший на семинаре Смолина в Гёттингене. Он говорит не об атомарности пространства и времени, а лишь об их квантованности.

Под этим термином я понимаю следующее. При квантовом измерении физической величины она квантуется, результатами ее измерения могут быть лишь дискретные (изолированные) значения. Например, кратные некоторого минимального ненулевого значения. Как заявил на одном форуме Петр Ильницкий: «Если я еще не все забыл, то мир дискретен в том смысле, что для всех величин существует минимальная величина дискретизации. Желающие могут искать «хвосты» начиная с квантовой механики, с самых основ. PS. 5 лет назад закончил Киевский университет, специальность – физика (кафедра теорфизики)». [Впрочем, с дискретностью всех возможных измеримых характеристик возникают уже математические проблемы. Например, пусть некоторая измеримая характеристика 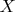квантовой частицы может принимать все натуральные значения. Возьмем две квантовые частицы и 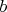, иррациональное число 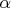и положим 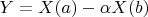. Тогда множество возможных значений характеристики 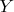уже недискретно. SS] В частности, могут квантоваться длина, площадь, объем (для пространства) и длительность (для времени). Впрочем, к квантованию измеримых величин меня склоняет уже то обстоятельство (О), что если мы проводим измерения посредством материальных (вещественных) инструментов, а материя квантована, то не будут ли и результаты этих измерений автоматически квантованы?

Akuklev иллюстрирует квантование измеримых величин так. «Весь сок квантовой механики в том, что квантованность некоторых величин происходит не потому что разрушилась непрерывность и гладкость подлежащей динамики, а потому-что процесс измерения «приводит» систему в одно из собственных состояний оператора измерения. Простейший пример: электрон со своим магнитным моментом. При помощи аппарата штерна-герлаха мы можем измерить магнитный момент электрона вдоль какой-нибудь выбранной оси. И получим 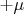или 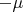, какую бы ось мы не выбрали. Говорят, что спин квантован и вдоль любой выбранной оси он может быть только «параллелен или антипараллелен оси», но имеется ввиду, что он становится таким в момент измерения. До измерения он произволен». Здесь я хотел бы заметить, что, почему бы тем направлениям оси, которые практически можно выбрать для постановки этого эксперимента, тоже, в свою очередь, не квантоваться?

Кроме того, как я понимаю, уже само квантовое измерение характеристики квантовомеханической системы может быть принципиально вероятностным актом. Т.е. результат измерения этой характеристики не определяется однозначно состоянием этой системы (которому соответствует волновая функция), но имеет уже вероятностное описание, в соответствии с правилами Борна.

Лично я думаю, что есть классические («редуцированные», «проявленные») состояния квантовых систем и есть специфически квантовые (рассматриваемые также как суперпозиции редуцированных), причем в момент измерения измеряемая система может принимать лишь классические состояния.

Akuklev утверждает, что в теории петлевой квантовой гравитации нет кванта длины, «длины могут быть сколь угодно малы. Зато есть кванты площади и объёма». Ли Смолин пишет, что «Главный вывод теории петлевой квантовой гравитации относится к объемам и площадям. Рассмотрим область пространства, ограниченную сферической оболочкой. В соответствии с классической (неквантовой) физикой ее объем может выражаться любым действительным положительным числом. Однако, согласно теории петлевой квантовой гравитации, существует отличный от нуля абсолютный наименьший объем (примерно равный кубу длины Планка, т.е. 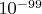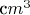), а значения больших объемов представляют собой дискретный ряд чисел. Аналогично, есть ненулевая минимальная площадь (примерно квадрат длины Планка или 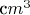) и дискретный ряд допустимых площадей большего размера. Дискретные спектры допустимых квантовых площадей и квантовых объемов в широком смысле похожи на дискретные квантовые уровни энергии атома водорода». Если квантование площади обусловлено Обстоятельством О, то, в этом свете, для меня неквантование длины выглядит несколько странным. Или в теории петлевой квантовой гравитации описываются не результаты измерения, а особенности расположения, т.е. метрики? Akuklev продолжает: «В случае квантованной геометрии, чистыми состояниями пространства-времени являются специальные трёхмерные обобщения графов, так называемые спиновые пены. (Название проистекает от мыльной пены, которая состоит из ячеек, отделённых друг от друга плоскими плёночками мыла, которые в свою очередь имеют форму многоугольников). Ну и выходит так, одна точка взаимодействия двух частиц может находиться где угодно в пространстве времени, две точки взаимодействия друг относительно друга тоже произвольным образом, однако три точки взаимодействия только таким образом, что площадь треугольника между ними всегда будет кратна определённому числу. Именно это подразумевается под квантованием пространства: взаимное расположение точек взаимодействия частиц не является независимым, причём определённые геометрические наблюдаемые имеют дискретный спектр». Это склоняет к относительности пространства, причем к какой-то странной относительности. Кроме того, поскольку случай лишь одной точки взаимодействия двух частиц является лишь мыслимым, но явно не реальным, то она вряд ли может находится «где угодно» в пространстве. Кстати, на диаграммах из статьи Ли Смолина дискретный ряд допустимых площадей не является рядом последовательных кратных.

dxdy.ru

Квантование пространства-времени

        общее название обобщений теории элементарных частиц (квантовой теории поля (См. Квантовая теория поля)), основанных на гипотезе о существовании конечных минимальных расстояний и промежутков времени, Ближайшей целью таких обобщений является построение непротиворечивой теории, в которой все физические величины получались бы конечными.

         Представления о пространстве и времени, которые используются в современной физической теории, наиболее последовательно формулируются в относительности теории (См. Относительности теория) А. Эйнштейна и являются макроскопическими, т. е. они опираются на опыт изучения макроскопических объектов, больших расстояний и промежутков времени. При построении теории, описывающей явления микромира, — квантовой механики (См. Квантовая механика) и квантовой теории поля, — эта классическая геометрическая картина, предполагающая непрерывность пространства и времени, была перенесена на новую область без каких-либо изменений. Экспериментальная проверка выводов квантовой теории пока прямо не указывает на существование границы, за которой перестают быть применимыми классические геометрические представления. Однако в самой теории элементарных частиц имеются трудности, которые наводят на мысль, что, возможно, геометрические представления, выработанные на основе макроскопического опыта, неверны для сверхмалых расстояний и промежутков времени, характерных для микромира, что представления о физическом пространстве и времени нуждаются в пересмотре.

         Эти трудности теории связаны с так называемой проблемой расходимостей: вычисления некоторых физических величин приводят к не имеющим физического смысла бесконечно большим значениям («расходимостям»). Расходимости появляются вследствие того, что в современной теории элементарные частицы рассматриваются как «точки», т. е. как материальные объекты без протяжённости. В простейшем виде это проявляется уже в классической теории электромагнитного поля (классической электродинамике (См. Электродинамика)), в которой возникает т. н. кулоновская расходимость — бесконечно большое значение для энергии кулоновского поля точечной заряженной частицы [из-за того, что на очень малых расстояниях r от частицы (г → 0) поле неограниченно возрастает].

         В квантовой теории поля не только остаётся кулоновская расходимость, но и появляются новые расходимости (например, для электрического заряда), также в конечном счёте связанные с точечностью частиц. (Условие точечности частиц в квантовой теории поля выступает в виде требования т. н. локальности взаимодействий: взаимодействие между полями определяется описывающими поля величинами, взятыми в одной и той же точке пространства и в один и тот же момент времени.) Казалось бы, расходимости легко устранить, если считать частицы не точечными, а протяжёнными, «размазанными» по некоторому малому объему. Но здесь существенные ограничения налагает теория относительности. Согласно этой теории, скорость любого сигнала (т. е. скорость переноса энергии, скорость передачи взаимодействия) не может превышать скорости света с. Предположение о том, что взаимодействие может передаваться со сверхсветовыми скоростями, приводит к противоречию с привычными (подтвержденными всем общечеловеческим опытом) представлениями о временной последовательности событий, связанных причинно-следственными соотношениями: окажется, что следствие может предшествовать причине. Конечность же скорости распространения взаимодействия невозможно совместить с неделимостью частиц: в принципе некоторой малой части протяжённой частицы можно было бы очень быстро сообщить столь мощный импульс, что данная часть улетела бы раньше, чем сигнал об этом дошёл бы до оставшейся части.

         Т. о., требования теории относительности и причинности (См. Причинность) приводят к необходимости считать частицы точечными, Но представление о точечности частиц тесно связано с тем, какова геометрия, принимаемая в теории, в частности, основывается ли эта геометрия на предположении о принципиальной возможности сколь угодно точного измерения расстояний (длин) и промежутков времени. В обычной теории явно или чаще неявно такая возможность предполагается.

         Во всех вариантах изменения геометрии большая роль принадлежит так называемой фундаментальной длине (См. Фундаментальная длина) l, которая вводится в теорию как новая (наряду

         с Планка постоянной (См. Планка постоянная) h и скоростью света

        с) универсальная постоянная. Введение фундаментальной длины l соответствует предположению, что измерение расстояний принципиально возможно лишь с ограниченной точностью порядка l (а времени — с точностью порядка l/c). Поэтому l называют также минимальной длиной. Если считать частицы неточечными, то их размеры выступают в роли некоторого минимального масштаба длины. Т. о., введение фундаментальной (минимальной) длины, в известном смысле, скрывает за собой неточечность частиц, что и даёт надежду на построение свободной от расходимостей теории.

         Одна из первых попыток введения фундаментальной длины была связана с переходом от непрерывных координат х, у, z и времени t к дискретным: х → n1l, y → n2l, z → n3l, t → n4l/c, где n1, n2, n3, n4 — целые числа, которые могут принимать значения от минус бесконечности до плюс бесконечности. Замена непрерывных координат дискретными несколько напоминает правила квантования Бора в первоначальной теории атома (см. Атом) — отсюда и термин«К. п.-в.».

         Если рассматривать большие расстояния и промежутки времени, то каждый «элементарный шаг» l или l/c можно считать бесконечно малым. Поэтому геометрия «больших масштабов» выглядит как обычная. Однако «в малом» эффект такого квантования становится существенным. В частности, введение минимальной длины l исключает существование волн с длиной λ l, т. е. как раз тех квантов бесконечно большой частоты ν = с/λ, а следовательно, и энергий ε = hν, которые, как показывает квантовая теория поля, ответственны за появление расходимостей. Здесь наглядно проявляется то, как изменение геометрических представлений влечёт за собой важные физические следствия.

         Введение указанным способом «ячеистого» пространства (с «ячейками» размера l) связано с нарушением изотропии пространства — равноправия всех направлений. Это один из существенных недостатков данной теории.

         Подобно тому, как на смену боровской теории (в которой условия квантования постулировались) пришла квантовая механика (в которой квантование получалось как естественное следствие основных её положений), за первыми попытками К. п.-в. появились более совершенные варианты. Их общей чертой (и здесь выступает аналогия с квантовой механикой, в которой физическим величинам ставятся в соответстие Операторы) является рассмотрение координат и времени как операторов, а не как обычных чисел. В квантовой механике формулируется важная общая теорема: если некоторые операторы не коммутируют между собой (т. е. в произведении таких операторов нельзя менять порядок сомножителей), то соответствующие этим операторам физические величины не могут быть одновременно точно определены. Таковы, например, операторы координаты x̅ и импульса частицы (операторы принято обозначать теми же буквами, что и соответствующие им физические величины, но сверху со «шляпкой»). Некоммутативность этих операторов является математическим отражением того факта, что для координаты и импульса частицы имеет место Неопределённостей соотношение:         

        показывающее границы точностей, с которыми могут быть одновременно определены px и х. Частица не может иметь одновременно точно определённые координату и импульс: чем точнее определена координата, тем менее определённым является импульс, и наоборот (с этим связано вероятностное описание состояния частицы в квантовой механике).

         При К. п.-в. некоммутирующими объявляются операторы, сопоставляемые координатам самих точек пространства и моментам времени. Некоммутативность операторов x̅ и , x̅ и и т.д. означает, что точное значение, например, координаты х в заданный момент времени t не может быть определено, так же как не может быть задано точное значение нескольких координат одновременно. Это приводит к вероятностному описанию пространства-времени. Вид операторов подбирается так, чтобы средние значения координат могли принимать лишь целочисленные значения, кратные фундаментальной длине l. Масштаб погрешностей (или неопределённость) координат определяется фундаментальной длиной.

         В некоторых вариантах теории постулируется непереставимость операторов координат и операторов, описывающих поле. Это равносильно предположению о невозможности одновременного точного задания описывающих поле величин и точки пространства, к которой эти величины относятся (такого рода варианты часто называют теориями нелокализуемых состояний).

         В большинстве известных попыток К. п.-в. сначала вводятся постулаты, касающиеся «микроструктуры» пространства-времени, а затем получившееся пространство «населяется» частицами, законы движения которых приводятся в соответствие с новой геометрией. На этом пути получен ряд интересных результатов: устраняются некоторые расходимости (однако иногда на их месте появляются новые), в некоторых случаях получается даже спектр масс элементарных частиц, т. е. предсказываются возможные массы частиц. Однако радикальных успехов получить пока не удалось, хотя методическая ценность проделанной работы несомненна. Представляется правдоподобным, что возникающие здесь трудности свидетельствуют о недостатках самого подхода к проблеме, при котором построение новой теории начинается с постулатов, касающихся «пустого» пространства (т. е. чисто геометрических постулатов, независимых от материи, это пространство «населяющей»).

         Пересмотр геометрических представлений необходим — эта идея стала почти общепризнанной. Однако такой пересмотр должен, по-видимому, в гораздо большей мере учитывать неразрывность представлений о пространстве, времени и материи.

         Лит.: Марков М. А., Гипероны и К-мезоны, М., 1958, §§33 и 34; Блохинцев Д. И., Пространство и время в микромире. М., 1970.

         В. И. Григорьев.

Поделитесь на страничке

slovar.wikireading.ru

Квантовая геометрия пространства-времени. Унификация моделей общей теории относительности и квантовой механики. Rafael Javier Маrtínez Оlmo

VTN= G • h • с-2 = 4,9205 ·10Е-55 сm +3· sg-1[3].

[1] У Вещественного числа (R) всегда есть бесконечное число десятичных чисел.

[2] У Rafaelian число R(N) всегда есть конечное число десятичных чисел.

[3] Фундаментальные физические постоянные, (G) Сила тяжести, (h) постоянная Planck, (c) скорость света.

Введение.

В течение многих столетий гипотеза, что вселенная продолжается {представленный только вещественными числами, устанавливала (R)}, который считали неоспоримой истиной. Не только вещество и энергию рассмотрели так, но также и пространство-время, которое содержит их.

С рождением квантовой механики мы поняли, что вещество не непрерывно (представленный (R) множества вещественных чисел. Например, алюминиевая панель не может быть разделена на мелкие кусочки, и их поочередно в меньшие, и так далее. Если бы мы продолжили разделять это, то только атом алюминия остался бы, и этот не может быть разделен на “1/x”, атомы алюминия.

Однако, так как атом не элементарен, мы можем даже разделить атомы алюминия. В контексте этой 'элементарной' работы означает, что это не имеет никаких частей и следовательно неделимо.

Атом может быть разделен на протоны, нейтроны и электроны.

Есть прочная гипотеза, что протоны и нейтроны не элементарны. Им составили внутреннюю структуру трех кварков. В настоящее время, нет никого, кто возвел гипотезу в степень, что кварк бесконечно делим.

У электрона нет внутренней структуры (у него нет никаких частей), и неделимо. Мы можем сказать, что это элементарно в смысле, выраженном(отжатом) в этой работе.

Квантовая механика также гарантирует, что энергия испущена и поглощена формой всего осторожного кванта; представленный только натуральными числами устанавливает (N).

Мы можем подтвердить, что гипотеза непрерывной вселенной ни не выполнена с веществом, ни с энергией. Когда я использую "непрерывный" термин или "непрерывность", я подразумеваю, что материальная действительность явления, чтобы описать может только быть представлена (R) множества Вещественных чисел.

Здесь вопрос возникает: Что произойдет, если пространство-время не было непрерывно? Что произойдет, если пространство-время не может быть представлено (R)?

Геометрия Пространства-времени

Предисловие

Мы знаем, что две фундаментальных теории на нашем понимании вселенной, Общей теории относительности и Квантовой механики, не являются правильными, так как они описывают два антагонистических мира, поэтому один из них, или возможно оба должны быть ошибочными.

Причина для бесконечностей, чтобы появиться, когда мы соединяем Общую теорию относительности и Квантовую механику, без возможности того, чтобы быть отщеплявшимся, (Общая теория относительности не, повторно подвергает нормализации), возникает в использовании (R) множество, чтобы описать физически вселенную.

Это, по моему мнению, основной принцип и предыдущая математическая причина, которая должна быть решена, чтобы достигнуть унификации обеих моделей; замена вещественных чисел (R) устанавливала R(N) множество представлять физически действительность.

Мы используем множество вещественных чисел, для обеих теорий, фактически для всей Физики. Это является неправильным, абсурдным и ненужным, так как это представляет математические понятия, не измеримы, такие как момент времени, точка, бесконечно малая, бесконечность. Мы должны помнить, что (R) - бесконечное множество второго порядка (Georg Cantor), то есть что это выполняет следование:

1. Его отсутствие элементов, которое порядковое число (N) присоединяло с каждым элементом (R), который указал бы Ваш порядковый номер согласно критерию построения множества.

Вещественные числа устанавливают (R) критерий отсутствий построения. Это отсутствие подразумевает, что никакой элемент (число) не существует в (R), который является предыдущим или последующим к любому другому элементу (число) (R). (Это - бесконечность второго порядка).

2. Использование (R) множества вещественных чисел подразумевает, что любое материальное измерение, такое как расстояние бесконечно делимо. Это означает тождественно, что расстояние, область, объем или количество времени, может принять, любое значение вещественных чисел устанавливало (R).

3. Во множестве вещественных чисел (R) часть множества имеет тот же самый размер, что все количество множества (R). В (R) часть равна целому.

Все эти свойства, по моему мнению, не существуют во Вселенной. Если мы используем R множества чисел (N)), эти три неестественных свойства исчезают. С этой целью, это достаточно, если мы бросаем идею, что у множества вещественных чисел есть десятичные разряды бесконечности (что физически мы не нуждаемся), и мы заменяем это R(N)), у которого есть достаточно большое количество десятичных разрядов.

Этот выбор (R), позволяет материальной переменной принимать любое значение, но это также подразумевает, что переменное значение может стоить бесконечности (особенность) и быть ограничено точкой это размерности отсутствий.

Гравитационные и электромагнитные силы являются обратно пропорциональными к квадрату расстояния между массами и электрическими материальными точками. Эти силы увеличиваются, когда расстояние уменьшается. Если эти расстояния, это - нуль, значение Материальных переменных (сила тяготения или электромагнитная сила) являются бесконечностью; (деление на нуль). Они - бесконечности та унификация препятствующей системы; это - погрешность, которую мы продолжаем делать; погрешность в основе Логики.

Эта погрешность появляется через математическую процедуру абстракции, которая заставляет геометрические тела меньших размерностей чем таковые Материального Вселенная появляться, то есть четыре, три пространственных размерности и временная размерность. Я имею в виду математические понятия точки, нулевой размерности, линия (определите размеры одного), плоскость (размерность два), объем без временного существования (размерность три), время без существования пространства (определите размеры одного), я также имею в виду математические понятия и материальное значение нуля и бесконечности.

Эта Погрешность находится в неоднозначности геометрической точки, когда применено к материальные понятия как расстояние, скорость, ускорение...

Понятие точки физически абсурдно, так как у этого есть два монопольных свойства; это существует или не существует.

Абсурдно думать, что материальные объекты существуют и не существуют. Однако, математическое понятие точки размерности = 0, когда это применено к физике, представляет этот парадокс:

Точка существует (физически). Поскольку у этого есть действительная и точная позиция в любой системе "пространства-времени" ссылки; который определен его четырьмя координатами в "пространстве-времени". Фактически точка используется, чтобы указать позицию в "пространстве-времени" (R4).

Точка не существует (физически). Поскольку у этого нет размерностей (размерность = 0). Это не имеет никакой высоты, никакой длины, никакой ширины, и не существует во время. Эта бессвязность является тонкой, но четкой после размышления.

У вселенной есть четыре размерности.

У пространства-времени есть четыре размерности.

Вещество имеет, всегда имеет три пространственных размерности (объем) и существует во время; энергия всегда занимает объем пространства и существует во время; поэтому у них обоих есть четыре размерности.

Абсолютный вакуум, недостающий и вещество и энергия, не существует. С тех пор нет никакого способа изолировать Силу тяжести объема "пространства-времени".

Относительный вакуум, который, по крайней мере, содержит Силу тяжести, имеет поэтому, четыре размерности. Нет никакого материального примера, (который существует и мог быть измерен), объектов в нашей вселенной, у которой нет четырех размерностей.

Следуя за Euclides, не возможно создать, просто добавляясь (сложение, сумма), геометрические тела различной размерности от ее элементов построения, и например, не возможно чертить линию, прибавляя достаточно большое число очков.

Если во Вселенной есть только элементы размерные четыре, у элементарного и неделимого элемента нашей вселенной должно быть четыре размерности, то есть, объем, который изменяется со временем.

Нет никаких объектов во Вселенной меньше чем четырех размерностей; они только существуют в Платоническом мире идей как математические абстракции действительности.

Чтобы вычислить значение самого низкого объема времени, мы используем фундаментальные константы вселенной, c, h, y G, таким же образом как Max Karl Ernst Ludwig Planck сделал столетие назад. Мы объединили их смотрящий в этом случае какое-то время объем, то есть объем поля в течение часа, например, единицы объема во время единицы времени. Это может быть сделано со следующей объединиликомбинацией фундаментальных констант, которая является также единственной:

www.gravityquantum.com

КВАНТОВАНИЕ ПРОСТРАНСТВА-ВРЕМЕНИ - это... Что такое КВАНТОВАНИЕ ПРОСТРАНСТВА-ВРЕМЕНИ?

-направление в квантовой теории поля (КТП), основанное на гипотезе о дискретной (квантованной) структуре пространственно-временного мира в области малых масштабов. Линейный размер "кванта пространства" интерпретируется как новая универсальная постоянная теории - фундаментальная длина (также элементарная, мин. длина) l. С точки зрения данного подхода стандартной КТП отвечает предельный случай l=0. Это находится в соответствии с принятой в КТП геом. концепцией пространства-времени, согласно к-рой микроскопич. пространственные расстояния качественно ничем не отличаются от макроскопических, а течение времени в ультракоротких интервалах такое же, как в интервалах произвольно большой длительности. Такая "классическая" геом. картина пока подтверждается всей совокупностью опытных данных, полученных в экспериментах с элементарными частицами, в т. ч. и при высоких энергиях. Частицы высоких энергий E>>mс2 ( т - масса частицы, с - скорость света) служат наиболее подходящим инструментом для зондирования возможной "зернистой" структуры пространства, т. к. им соответствует диапазон очень коротких волн де Бройля-~hc/E (h - постоянная Планка), позволяющих "видеть" сверхмалые расстояния. Эксперим. обнаружение нового фундам. масштаба l, свидетельствующего о существовании специфич. атомизма пространства-времени, означало бы, что в познании природы сделан новый шаг, соизмеримый по своему значению с открытием квантовых свойств материи. Пока, однако, гипотеза о К. п.-в. опирается лишь на теоретич. аргументы. Самый популярный из них - существование в стандартной КТП т. н. ультрафиолетовых расходимостей, т. е. бесконечно больших величин, возникающих в результате прямого применения ур-ний КТП в области очень малых пространственно-временных расстояний, или, что эквивалентно, в области очень больших энергий и импульсов. Было замечено, что указанные расходимости не появляются вовсе, если сверхмалые расстояния исключить из теориис самого начала. Этого можно достичь, напр., путём замены непрерывного пространства-времени четырёхмерной решёткой, узлам к-рой отвечают дискретные значения координат и времени: x=n1l, y=n2l, z=n3l, t=n4.l/c(n1,. . ., n4 - произвольные целые числа). Однако в такой теории отсутствует релятивистская инвариантность, нарушаются стандартные законы сохранения энергии, импульса, момента импульса. Совр. версии таких теорий - т. н. калибровочные теории квантового поля на решётке (см. Решетки метод) - применяются в качестве схем, позволяющих понять на качеств. уровне специфику калибровочных КТП, а также используются в квантовой хромoдинамике для расчётов на ЭВМ методом Монте-Карло. к-рые могут быть выбраны так, что либо либо каждая из величин имеют целочисленный спектр собственных значений в единицах l/с и l соответственно. В матем. отношении здесь имеется аналогия с квантовомеханич. теорией момента количества движения. к диагональному виду чрезвычайно затрудняет развитие аппарата КТП в таком квантованном пространстве-времени. Оказывается, однако, что пространство энергии-импульса в данном случае является разновидностью четырёхмерного пространства Лобачевского и может служить адекватной основой для последовательной релятивистской формулировки КТП, в к-рой выполнены все стандартные законы сохранения. При этом постоянная l, определяющая кривизну импульсно-энергетич. пространства Лобачевского, с самого начала выступает как фундам. параметр теории. В области "сравнительно небольших" энергий E<<hc/l новая теория совпадает с прежней. Но при "сверхвысоких" энергиях E/hc/l мн. её выводы и предсказания кардинально отличаются от того, что вытекает из традиционной КТП. квантовая электродинамика, квантовая хромодинамика, теория электрослабого взаимодействия и т. д.- принадлежат к классу т. н. перенормируемых теории, в к-рых существование расходимостей не мешает проведению количеств. расчётов с любой степенью точности. Успехи этих теорий в описании имеющихся эксперты, данных не являются аргументом против существования фундам. длины l. Они свидетельствуют лишь о том, что совр. физика высоких энергий ещё далеко отстоит от того рубежа, за к-рым могут проявиться новые геом. свойства пространства-времени. Лит.: В я л ь ц е в А. Н., Дискретное пространство-время, М., 1965; Блохинцев Д. И., Пространство и время в микромире, М., 1970; Кадышевский В. Г., Квантовая теория поля и импульсное пространство постоянной кривизны, в кн.: Проблемы теоретической физики, М., 1972, с. 52; Кадышевский В. Г., Новый подход к теории электромагнитных взаимодействий, "ЭЧАЯ", 1980, т. 11, с. 5. В. Г. Кадышевский.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.

dic.academic.ru

---

• 
  Первый высказал предположение о квантовой природе света
• 
  Квантовый дуализм
• 
  Квантовое шифрование
• 
  Эксперимент с двумя щелями квантовая физика
• 
  Квантовая теория поля для чайников
• 
  Принцип причинности в квантовой механике
• 
  Квантовое существование
• 
  Квантовый мир и сознание
• 
  Теория относительности и квантовая механика
• 
  Квантовая флуктуация
• 
  Квантовые отношения